The Recursion Pattern

Recursion

: 어떤 함수가 자기자신을 부르는 구조

Ex. factorial function

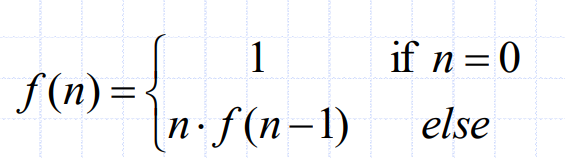
def factorial(n):
	if n == 0: # base case
    	return 1
    else: # recursive calls
    	return n * factorial(n-1)

• Base case(s)
  : 필수적으로 1개는 있어야함
  : 기본 케이스
• Recursive calls
  : 현재 메서드를 호출

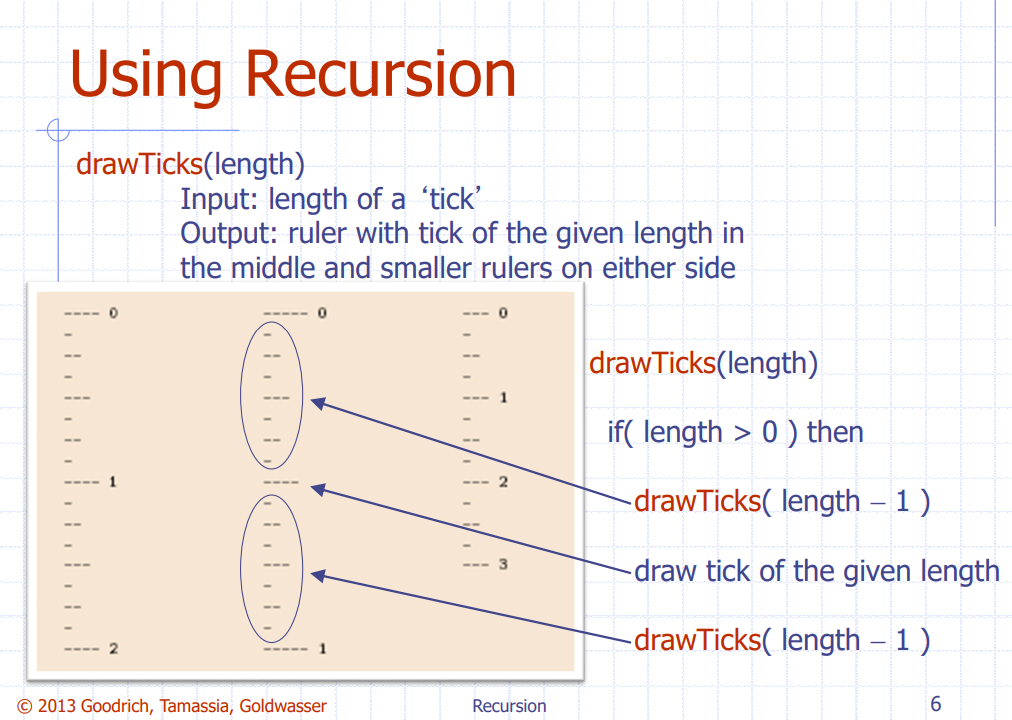
Ex. English Ruler

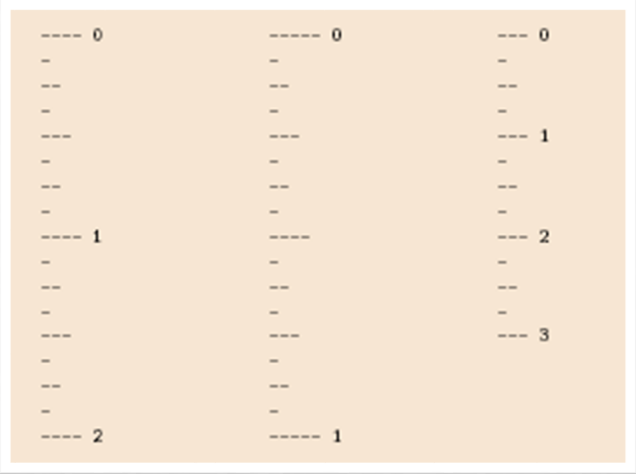
cf. ----- 는 -가 5개 이므로 5tick = length 5

class EnglishRuler:
    def __init__ (self, num_inches, major_length):
        self.__num_inches = num_inches # inch의 개수
        self.__major_length = major_length # 길이

    def draw_line(self, tick_length, tick_label=''):
        # 단일 눈금을 그리는 메서드
        # 그려진 라인에 눈금 레이블(정수)를 추가하는 조건문 실행
        line = '-' * tick_length
        if tick_label:
            line += '' + tick_label
        print(line)

    def draw_interval(self, center_length):
        if center_length > 0:
            self.draw_interval(center_length-1)
            self.draw_line(center_length)
            self.draw_interval(center_length-1)

    def draw_ruler(self):
        self.draw_line(self.__major_length, '0')
        for j in range(1, 1+self.__num_inches):
            self.draw_interval(self.__major_length-1)
            self.draw_line(self.__major_length, str(j))

if __name__ == '__main__':
    rule = EnglishRuler(2,3)
    rule.draw_ruler()

Binary Search

def binary_search(data, target, low, high:
	if low > high:
    	return False
    else:
    	mid = (low + high) // 2
        if target == data[mid]:
        	return True
        elif target < data[mid]:
        	retun binary_search(data, target, low, mid-1)
        else:
        	return binary_search(data, target, mid + 1, high)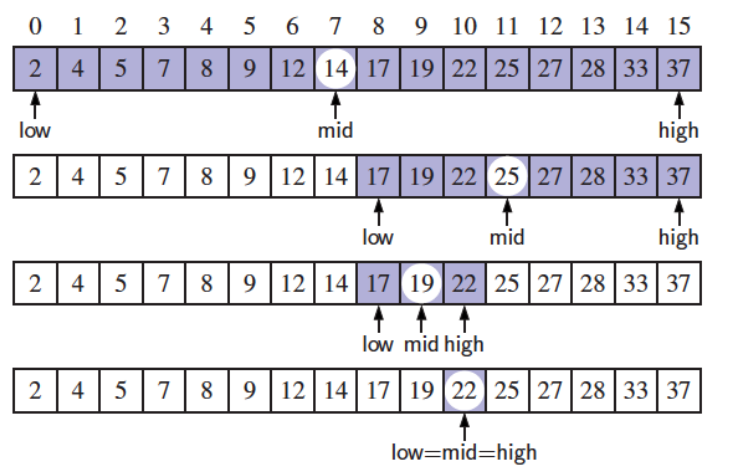

Analyzing Binary Serach → O(log n)

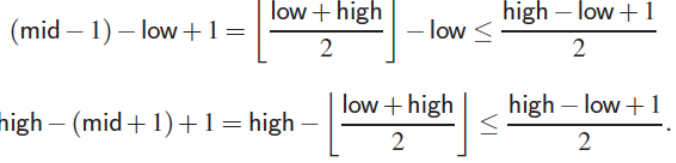
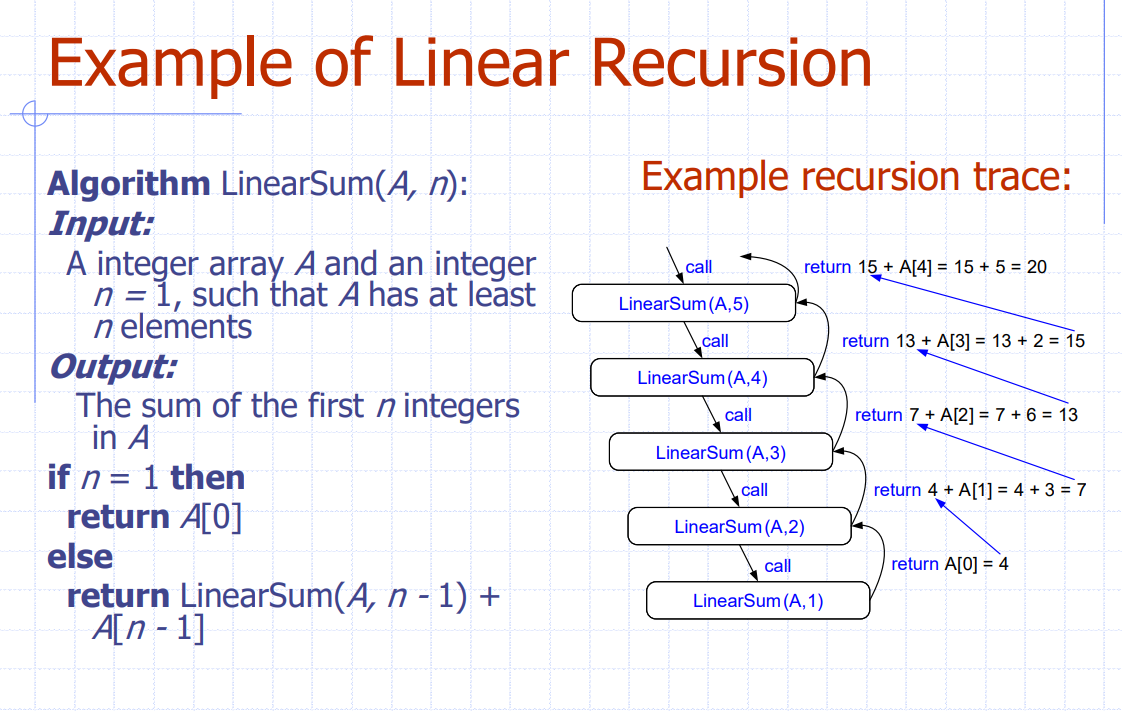
Linear Recursion

• 우리가 흔히 아는 재귀 호출
• 한번의 호출에 1번 자기 자신을 호출
  

Reversing an Array

Defining Arguments for Recursion

def reverse(S, start, stop):
	if start < stop - 1:
    	S[start], S[stop-1] = S[stop-1], S[start]
        reverse(S, start+1, stop-1)
        

Computing Powers

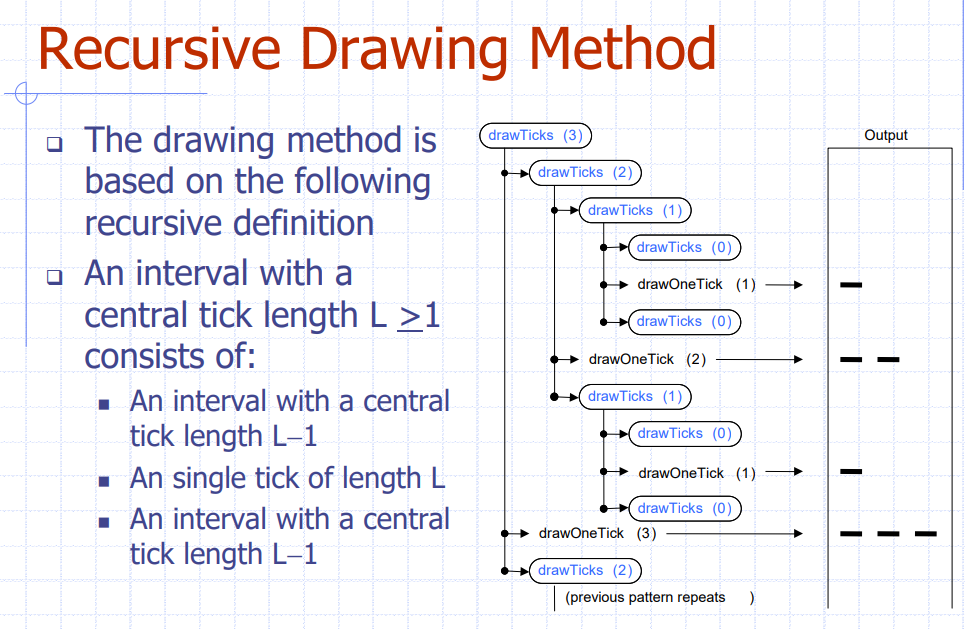
Binary Recursion

• 한번의 호출에 2번 자기 자신을 호출

DrawTicks method is Binary Recursion!

Another Binary Recursive Method

Computing Fibonacci Numbers

→ exponential function!😓

A Better Fibonacci Algorithm

Multiple Recursion

• 한번의 호출에 다수의 자기 자신을 호출