노드(vertice)와 간선(정점/edge/arcs)로 이루어진 자료 구조.
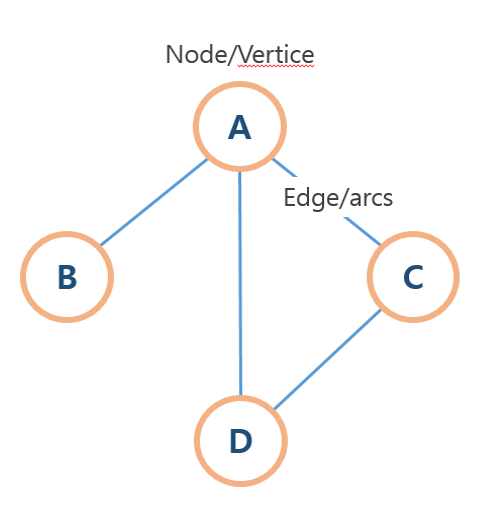
그래프 용어
-
노드(node) : 정점(vertice)라고도 불리며, 일반적으로 노드에는 데이터가 저장됨
-
간선(edge): 링크, arcs라고도 불리며, 노드간의 관계를 나타냄
-
인접 정점(adjacent vertex) : 간선에 의해 연결된 정점. 위 그림에서 노드A와 B는 인접 정점이라고 할 수 있다
-
단순 경로(simple-path): 경로 중 반복되는 정점이 없는것, 같은 간선을 자나가지 않는 경로
-
차수(degree): 무방향 그래프에서 하나의 정점에 인접한 정점의 수. 위 그래프에서 A의 차수는 3이다.
-
진출차수(out-degree)/진입차수(in-degree) : 방향그래프에서 사용되는 용어
진출 차수 는 한 노드에서 외부로 향하는 간선의 수,
진입차수 는 외부 노드에서 들어오는 간선의 수
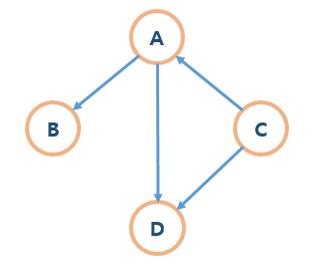
위 그래프의 A노드에서 진출차수는 2, 진입차수는 1이다.
그래프의 특징
그래프는 네트워크 모델 즉, 객체와 이에 대한 관계를 나타내는 유연한 방식으로 이해할 수 있다.
그래프의 순회는 DFS(깊이 우선 탐색), BFS(너비 우선 탐색)으로 할 수 있다.
그래프에는 루트 노드, 부모-자식이라는 개념이 없다
그래프마다 간선이 없을수도 있고, 있을수도 있다.
트리는 그래프의 한 종류이다.
그래프의 종류
방향그래프, 무방향그래프
-
방향 그래프(Directed Graph)
간선에 방향성이 추가된 그래프이다. 위 그래프의 흐름은 A에서 B로 진행되며, <A,B>로 표기할 수 있다.
ex) 일방통행 도로, 한 번 지나가면 무너지는 다리
-
무방향 그래프(Undirected Graph)

방향성이 없는 그래프이다. A에서 B로, B에서 A로도 갈 수 있으며 (A,B)로 표기할 수 있다.
ex) 양방향 도로, 일반적인 길 등
가중치 그래프

그래프 간선에 비용/가중치가 부여되어있는 그래프이다.
ex) 각 섬 사이를 지나는데 걸리는 시간 등
사이클, 비순환 그래프
-
사이클(Cycle)
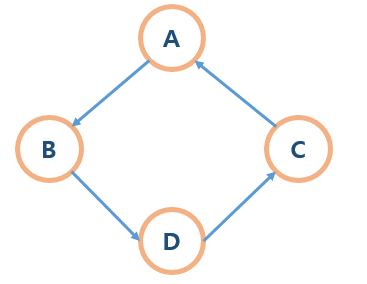
단순 경로에서 시작 정점과 도착 정점이 동일한 그래프이다. 위 사진에서는 A에서 시작하여 A로 끝난다.
-
비순환 그래프
사이클 그래프를 제외한 그래프로, 사이클이 없는 그래프이다.
완전 그래프, 부분 그래프
-
완전 그래프
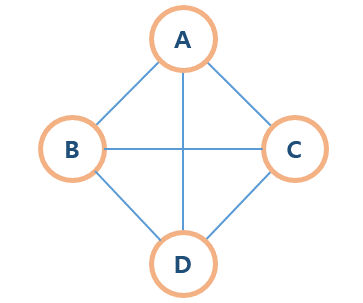
모든 정점이 서로 연결되어있는 그래프이다. -
부분 그래프
완전 그래프가 아닌, 그래프는 부분 그래프이다.
연결 그래프, 비연결 그래프
-
연결 그래프
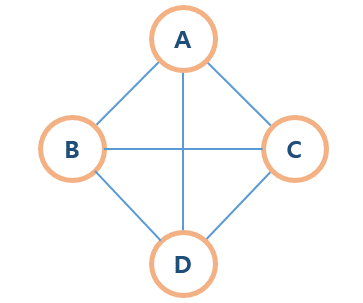
노드들이 하나도 빠짐없이 간선에 의해 연결되어 있는 그래프이다. -
비연결 그래프
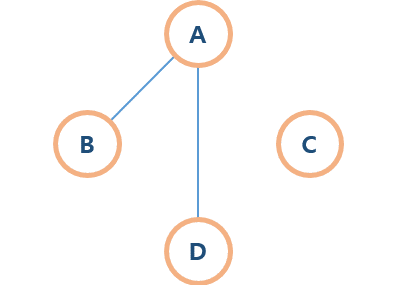
노드들 중, 간선에 의해 연결되어있지 않은 노드가 있는 그래프이다.
신장 트리(Spanning Tree)
- 그래프의 모든 정점을 포함하는 트리
- 그래프의 최소 연결 부분 그래프(간선의 수가 제일 적은 그래프)
- 그래프에서 일부 간선의 채택하여 만든 그래프
- 하나의 그래프에선 여러개의 신장 트리가 나올 수 있다
- 트리의 특수한 형태, 사이클을 포함해선 안된다.
최소 신장 트리(Minimal Spanning Tree/ MST)
- 각 간선에 가중치가 부여되어 있을 때, 가중치를 고려하여 최소 비용의 신장트리를 구하는 것
- 크루스칼, 프림 알고리즘을 이용해서 구할 수 있다.
비순환 방향 그래프
- 순환하지 않고(사이클 그래프가 아님. 즉, 어떻게 되는 시작노드와 끝나는 노드가 다름) 방항성만 갖는 것
- 트리가 여기에 속해있다
그래프 구현 방법
인접 행렬
인접 행렬은 이차원 배열 을 이용하는 방식이다.
완성된 배열의 모양은 A, B, C, D 노드에 다른 노드들이 인접 정점이라면 1, 아니면 0을 넣어준다.
즉,
if(노드 i,j를 잇는 간선이 그래프에 존재) {
M[i][j] = 1;
}
else{
M[i][j] = 0;
}이렇게 표현할 수 있다. 여기서 노드 i,j는 그림의 a, b, c, d 노드들을 숫자 1, 2, 3, 4로 표현한것 이라고 볼 수 있다.
구현하기 쉽다는 장점이 있지만, 인접 리스트보다는 느리다라는 단점이 있다.
노드 개수의 제곱에 해당하는 공간을 차지한다. O(n) 이다
인접 리스트
인접 리스트는 연결리스트를 이용한다.
연결리스트로 표현해서, 각 노드에 인접하게 연결되어있는 노드들을 순서에 상관없이 이어준다.
인접 행렬보다빠르다 라는 장점이 있지만, 인접 행렬보다 구현하기 어렵다라는 단점이 있다.
연결된 간선만의 정보를 저장해서 간선의 개수 만큼의 공간을 차지한다. O(n^2)이다.
간선이 m일때, 총 노드의 수는 2m개이다.
