📝새롭게 배운것

1. 자바 개념에서 배웠던 비트 연산자를 이용한 순열 알고리즘을 공부했습니다.

2. 사전식으로 다음으로 큰 순열을 생성해 주는 NextPermutation이라는 알고리즘 개념을 새로 공부했습니다.

• 알고리즘은 다음 과정을 반복한다.
  stet 1. 뒤쪽부터 탐색하며 교환위치(i-1) 찾기
  step 2. 교환위치(i-1)와 교환할 큰 값 위치(j) 찾기
  step 3. 두 위치 값(i-1, j) 교환
  step 4. 교환위치 이후를 오름차순 정렬

순열(Permutation)

서로 다른 것들 중 몇 개를 뽑아서 한 줄로 나열하는 알고리즘

기존 방문처리를 이용한 순열

static int N,R;
static int[] input, numbers;
static boolean[] selected;
private static void permutation(int cnt) {
	if(cnt == R) {
		System.out.println(Arrays.toString(numbers));
		return;
	}
	for(int i=0; i<N; ++i) {
		if(selected[i]) continue;
		numbers[cnt] = input[i];
		selected[i] = true;
		permutation(cnt+1);
		selected[i] = false;
}

비트 연산을 이용한 순열

비트연산자

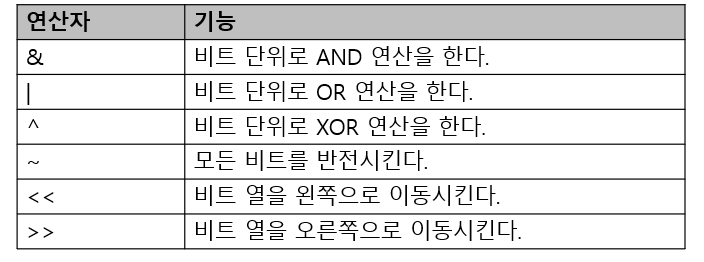
✔ 참고

• 1 << n : 2^n 값을 갖는다.
• i & (1<<j) : i의 오른쪽에서 j번째 비트가 1인지 확인한다.
• i | (i<<j) : i의 기존 비트열의 오른쪽에서 j번째 비트를 1로 변경한다.

private static void permutation(int cnt, int flag) {
	if(cnt == R) {
		totalCount++;
		System.out.println(Arrays.toString(numbers));
		return;
	}
	for(int i=0; i<N; ++i) {
		if((flag&(1<<i)) != 0) continue;
		numbers[cnt] = input[i];
		permutation(cnt+1, (flag|(1<<i)));
	}
}

NextPermutation

public class NextPermutationTest {

	// 1,2,3
	// 3P2 = 3!/1!= 6
	// 1,2,3
	// 3P3 = 3!
	static int N,R;
	static int[] input;
	static int totalCount;
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		N = sc.nextInt();
		R = sc.nextInt();
		input = new int[N];

		for (int i = 0; i < N; i++) {
			input[i] = sc.nextInt();
		}
		
		Arrays.sort(input);
		
		do {
			System.out.println(Arrays.toString(input));
		}while(nextPermutation(input));
	}

	private static boolean nextPermutation(int[] numbers) {

		// step1. 꼭대기 찾기
		int i = N-1;
		while(i>0 && numbers[i-1] >= numbers[i]) --i;
		if(i == 0) return false;  // 마지막 순열 상태이면 다음 순열 없음
		
		// setp2. i-1 위치와 교환할 다음 단계 큰 수를 뒷쪽에서 찾기
		int j = N-1;
		while(numbers[i-1] >= numbers[j]) --j;
		
		//step3. i-1 위치값과 j 위치값 교환
		swap(numbers, i-1, j);
		
		//step4. i 위치부터 맨 뒤까지 오름차순 정렬
		int k = N-1;
		while(i<k) {
			swap(numbers, i++, k--);
		}
		return true;
	}
	
	public static void swap(int[] numbers, int i, int j) {
		int tmp = numbers[i];
		numbers[i] = numbers[j];
		numbers[j] = tmp;
	}
}