1. 딥러닝 용어

1) 구조

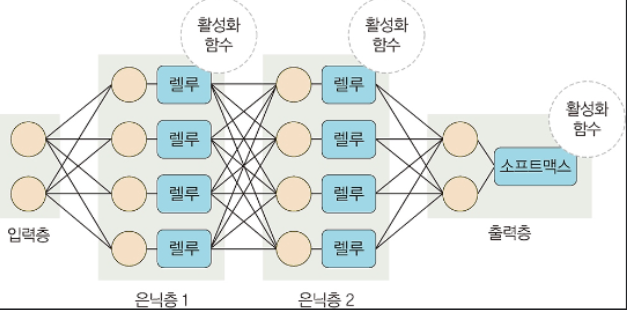
• 딥러닝은 입력층, 은닉층 , 출력층으로 구성

• 입력층 : 데이터를 받아들이고. 입력값을 은닉층으로 전달하는 층

• 은닉층 : 입력받은 데이터를 가중치와 bias에 따라 연산하는 층.
  층이 여러개이면 다층 신경망
  

• 출력층 : 신경망의 최종 결괏값이 포함된 층

2) 가중치

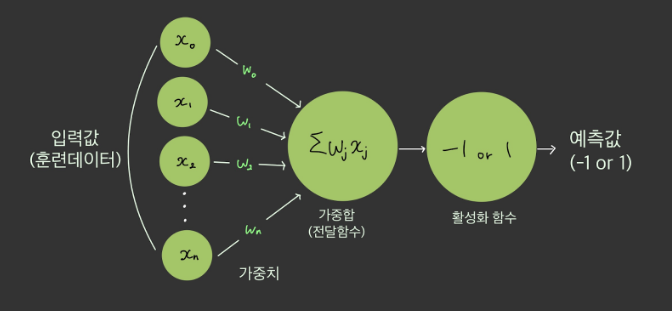
• 입력값이 연산결과에 미치는 영향력을 조절하는 요소
• 그림에서 w1 값이 0이나 0에 가까울 경우, x1이 아무리 큰 값이여도
  w1 * x1은 0이거나 0에 가까운 값이 될 것이다.
• 이와 같이 입력값의 연산 결과를 조정해조정해주는 역활을 한다.

3) 가중합

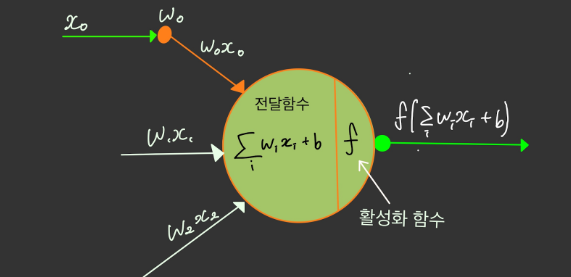
• 각 노드에서 들어오는 신호에 가중치를 곱해 다음 노드로 전달되는데, 이 값들을 모두 더한 것을 가중합이라고 한다.
• 노드의 가중합이 계산되면 이 가중합을 활성화 함수로 보내기 때문에 전달함수라고도 한다.

4) bias

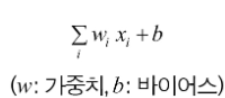
• b는 바이어스로 가중합에 더해주는 상수 이다.
• 하나의 뉴런에서 활성화 함수를 지나 최종적으로 출려되는 값을 조절.

---

2. 활성화 함수

• 전달받은 값을 출력할 때 일정 기준에 따라 출력 값을 변화시키는 비선형 함수.
• 시그모이드, 하이퍼볼릭 탄젠트, 렐루 함수 등이 있다.

❓활성화 함수는 선형이 아닌 비선형 함수를 사용하는지??

• 선형함수로 하게 되면 신경층망을 깊게 하는 의미가 줄어든다. 즉, 은닉층 없는 네트워크로도 똑같은 기능을 할 수 있다.
  
  예를 들어 선형함수인 h(x)=cx를 활성화 함수로 사용한 3층 네트워크일 경우
• yx = h(h(h(x))) = c c c * x = c^3x 이 된다
• 이는 y = ax에서 a = c^3인 선형이며 1층으로 구성된 네트워크와 다를 것이 없어진다.

선형함수 : 출력이 입력의 상수 배만큼 변화하는 함수(1개의 직선)
비선형 함수 : 선형이 아닌 함수로 1개의 직선으로 그릴 수 없는 함수

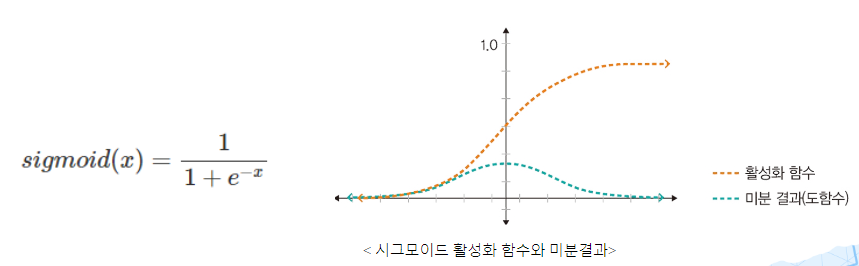
1) 시그모이드 함수

• 시그모이드 함수는 선형 함수의 결과를 0 ~ 1사이에서 비선형 형태로 변형.

• 주로 로지스틱 회귀와 같은 분류 문제를 확률적으로 표현하는데 사용

• 과거 인기가 많았으나, 모델의 깊이가 깊어지면서 기울기가 사라지는
  기울기 소멸 문제가 발생하여 딥러닝 모델에서 잘 사용하지 않음

• 장단점을 살펴보면 출력값이 작아서 제대로 학습이 되지 않고 시간이 많이 들어 출력층에서 사용은 문제 없지만, 은닉층에서는 안쓰는게 좋다고 함.

2) 하이퍼볼릭 탄젠트 함수

• 선형 함수의 결과를 -1 ~ 1사이에서 비선형 형태로 변형
• 시그모이드나 소프트맥스 함수의 경우 유명하고 로지스틱 회귀 모형에서 유래되었기에 자세하게 공부할 가치가 있음에 하이퍼볼릭은 그 정도까지 필요없다고 함,,,

❗ 하이퍼볼릭 탄젠트 함수와 시그모이드 함수 비교

• 하이퍼볼릭 탄젠트는 -1 ~ 1 로 중앙값이 0이기 때문에 경사하강법 사용시 편향이동이 발생하지 않음.
  -> 즉, 기울기가 양수 음수 모두 나올 수 있어 시그모이드 보다 학습효율성이 뛰어남.
  
  
  
• 시그모이드보다 하이퍼볼릭 탄젠트가 법위가 넓어 출력값의 변화폭이 크기에 기울기 소실 증상이 적음
• 은닉층에서 시그모이드 함수의 역활을 하는 레이어를 쌓고 싶다 할 때 사용하면 좋음
• 하지만 시그모이드보다 범위가 넓을 뿐. 하이퍼볼릭탄젠트 역시 구간이 크지 않아 기울기 소실 문제는 여전히 발생.

3) 렐루 함수

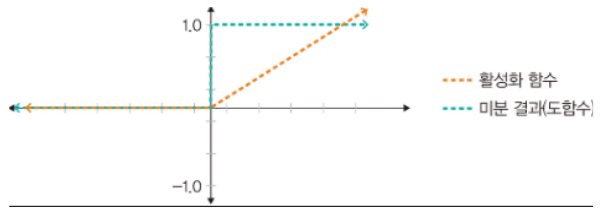
• 입력이 음수일때 0을 출력, 양수일 때는 x를 출력
• 강사하강법에 영향을 주지 않아 학습속도가 빠르고 기울시 소멸 문제가 발생하지 X
• 주로 은닉층에서 사용하며 하이퍼볼릭 탄젠트 함수 대비 학습속도가 6배 빠르다고 함
• 하지만 음수 값을 받으면 항상 0을 출력해 학습능력이 감소하는 것인데 이를 해결 하기 위해 리키렐루 등을 사용한다고 함.

4) 소프트맥스 함수

• 세개 이상으로 분류하는 다중 클래스 분류에서 사용되는 활성화 함수
• 입력값을 0~1사이에 출력되도록 정규화하여 출력값 총합이 항상 1이 되도록 함.
• 분류될 클래스가 N개라고 할 때, N 차원의 벡터를 입력받아 각 클래스에 속할 확률을 추정.
• 출력층에서 주로 사용.

❗소프트맥스 함수 수식

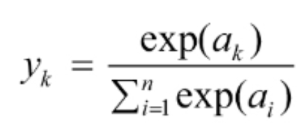
• n = 출력층의 뉴런 개수
  yk = k번째 출력
  exp(ak) and exp(ai) = 지수함수(exponential function)
• 즉 소프트맥스함수의 분자는 입력신호 ak의 지수함수, 분모는 모든 입력 신호의 지수함수의 합으로 구성.