Loss: 실제 값과 예측 값 차이

import torch
import torch.nn as nn

y_true = torch.randn(1, 5)
y_pred = torch.randn(1, 5)

print(y_true) # tensor([[-0.2096, -0.3947, -0.6602, -0.1333, -0.2629]])
print(y_pred) # tensor([[0.1915, 1.8731, 1.1904, 0.7739, 0.7772]])

L1, L2 Loss

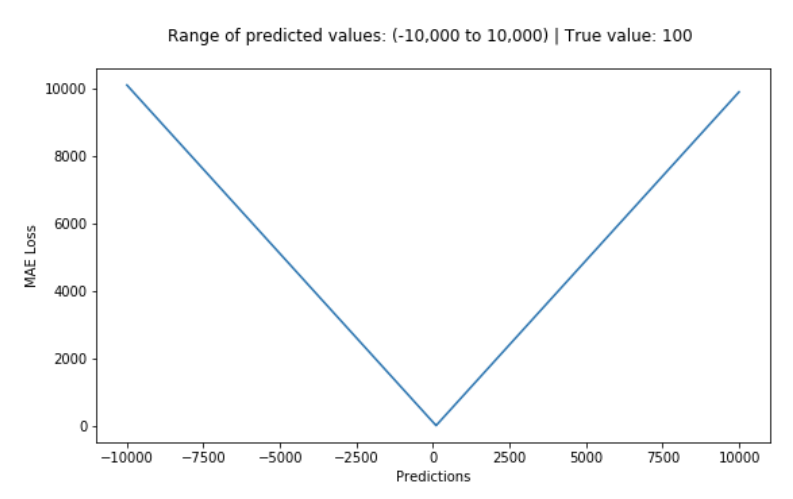
L1 Loss

L1 Loss의 경우, 'V' 형태로 미분 불가능한 지점이 있지만 상대적으로 L2 Loss에 비해 이상치에 대한 영향은 적다.

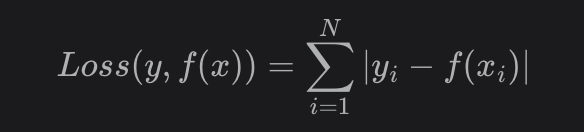
import torch
import torch.nn as nn

y_true = torch.randn(1, 5)
y_pred = torch.randn(1, 5)

print(y_true) # tensor([[-0.2096, -0.3947, -0.6602, -0.1333, -0.2629]])
print(y_pred) # tensor([[0.1915, 1.8731, 1.1904, 0.7739, 0.7772]])

L2 Loss

L2 Loss의 경우, 'U' 형태로 모든 지점에서 미분 가능하지만, 이상치의 에러가 제곱이 되기 때문에 이상치에 취약한 단점이 있다.

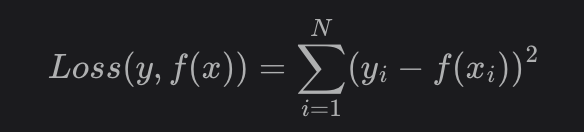
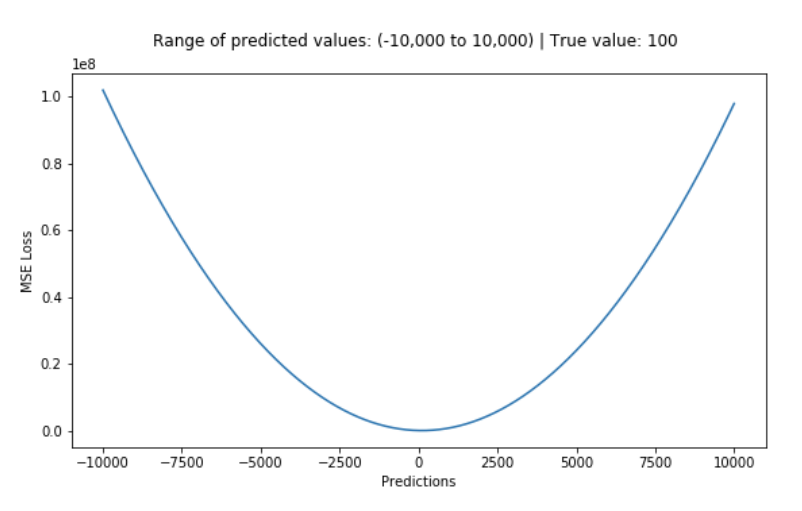
mse_loss = nn.MSELoss(reduction='sum')
loss = mse_loss(y_true, y_pred)
print(loss) # tensor(10.6334)

Huber Loss

L1과 L2의 장점을 취하면서 단점을 보완하기 위해 제안된 것이 Huber Loss이다.
Huber loss는 모든 지점에서 미분이 가능하면서 이상치에 강건한(robust) 성격을 보인다.

수식

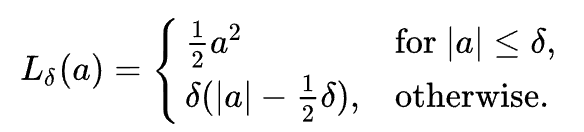
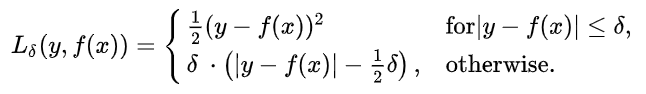
huber_loss = nn.HuberLoss(reduction='sum')
loss = huber_loss(y_true, y_pred)
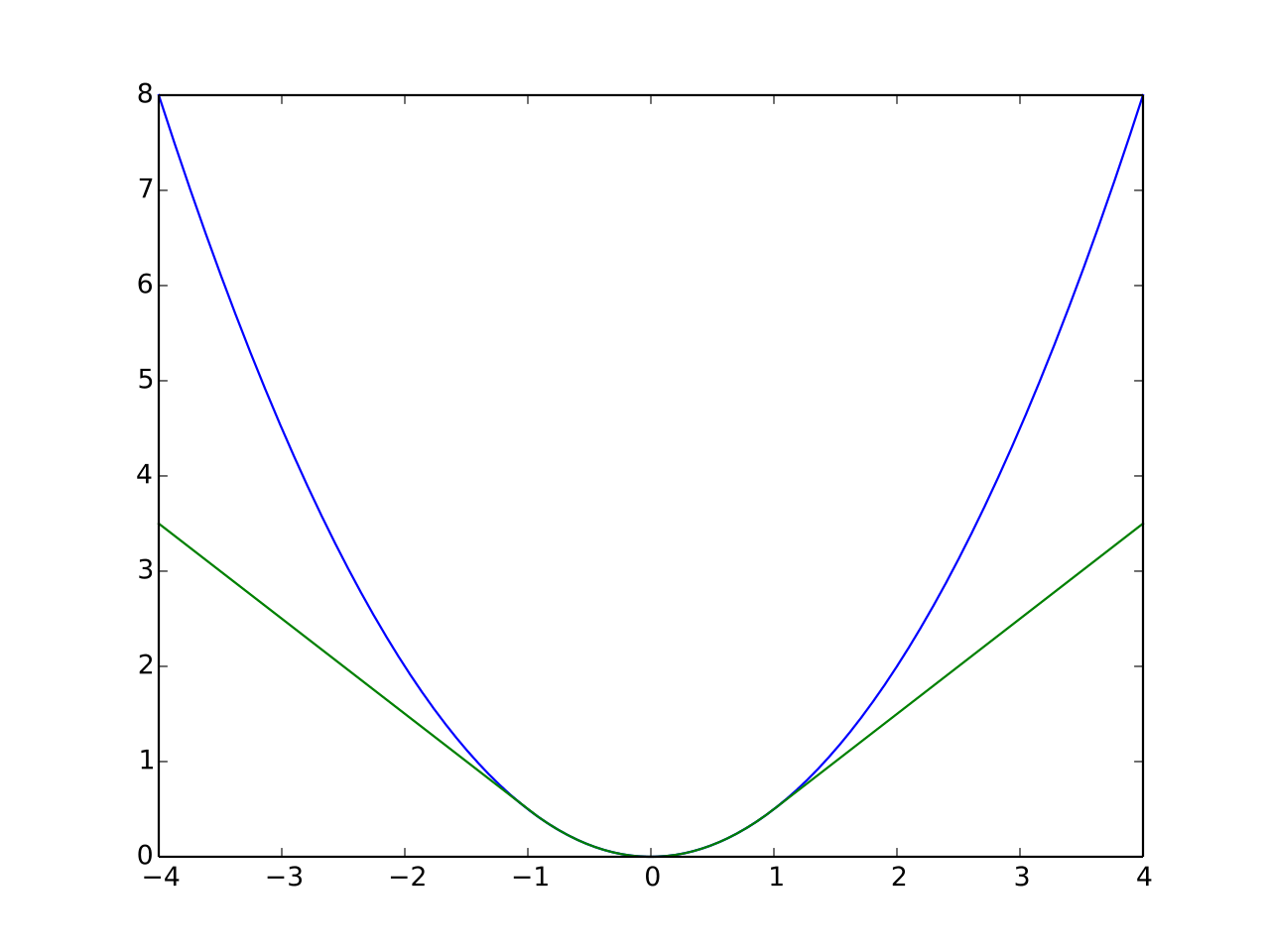
print(loss) # tensor(4.1505)

Huber Loss(Green) vs L2 Loss(Blue)

아래 그림은 $\delta$를 1로 설정했을 때, Huber loss(Green)와 L2 Loss(Blue)다. -1, 1사이에서는 Huber loss와 L2 loss가 유사하지만 그 외의 부분은 L1 loss와 유사한 형태를 보인다.

참고

• Huber Norm, Huber Loss
• 모든 기계 학습자가 알아야 할 5 가지 회귀 손실 함수
• Huber Loss & F.smooth-l1-loss()
• MSE Loss (L2 Loss) vs. MAE Loss (L1 Loss)