선행 지식
계산 그래프, 연쇄법칙, 역전파와 관련된 내용이 궁금하다면, 아래 포스팅을 참조하자.
Softmax-with-Loss 계층
softmax-with-loss 계층의 계산그래프는 아래와 같다.
이전 계층으로부터 입력은 (a1,a2,a3)이며, Softmax 계층은 (y1,y2,y3)를 출력한다. 정답 레이블은 (t1,t2,t3)이며 cross entropy error 계층은 손실 L을 출력한다.
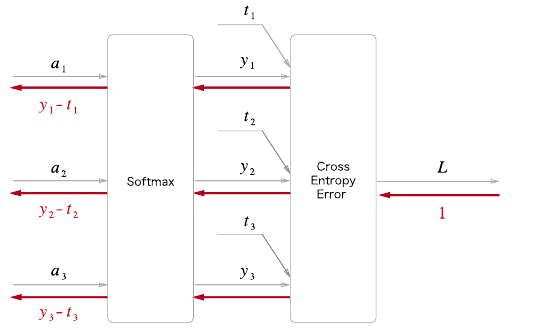
Softmax 계층 계산 그래프 (순전파)
Softmax 수식은 다음과 같다.
yk=∑i=1nexp(ai)exp(ak)
위 식을 바탕으로 Softmax 계산 그래프는 다음과 같다.

Cross Entropy Error 계층 계산 그래프 (순전파, 역전파)
Cross Entropy Error 수식은 다음과 같다.
L=−k∑tklog(yk)
위 식을 바탕으로 Cross Entropy Error 순전파 계산 그래프는 다음과 같다.

반대로 역전파 그래프는 다음과 같다.
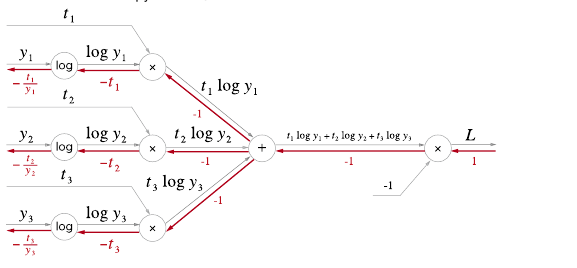
'log'노드의 역전파는 다음 식을 따른다.
δxδy=x1
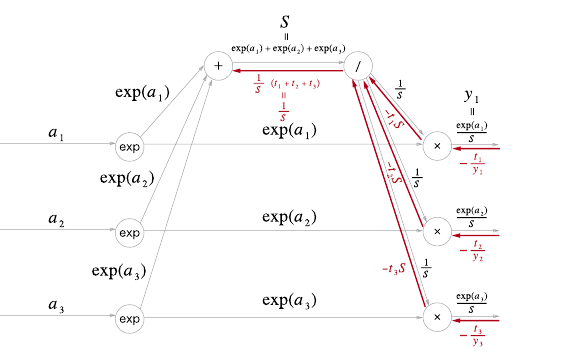
Softmax 계층 계산 그래프 (역전파)
위에서 구한 cross entropy error 역전파 값이 흘러 들어온다.

'X' 노드에서는 순전파의 입력들을 '서로 바꿔서' 곱한다.
아래 그림에서 위 '/' 노드로 가는 값은 다음과 같은 계산이 이루어진다.
−y1t1exp(a1)=−t1exp(a1)Sexp(a1)=−t1S

상류로 들어온 값은 (−t1S)+(−t2S)+(−t3S)=−S(t1+t2+t3)이다.
순전파의 출력은 S1이므로 역전파의 출력은 S1의 미분 값인 −S21를 곱해야한다.
따라서 −S(t1+t2+t3)∗−S21=S1(t1+t2+t3)가 된다.
또한 (t1,t2,t3)은 정답레이블로 원-핫 벡터로 표현되어 있다.
따라서 t1+t2+t3=1이 된다.
즉 역전파의 출력은 S1가 된다.
'+' 노드는 입력을 여과 없이 내보낸다.

'x' 노드는 입력을 서로 바꾼 곱셈이다.
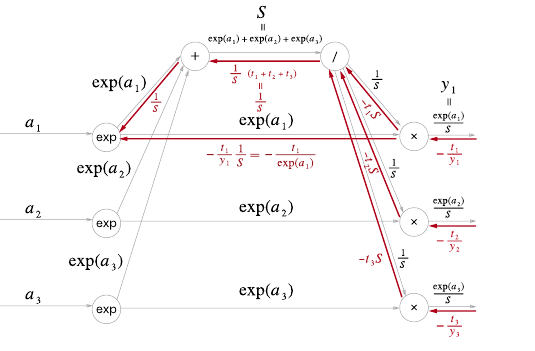
exp 노드에서는 exp함수가 미분해도 exp(x) 이기 때문에 각 갈래의 입력의 합에 exp(a1)을 곱한 결과가 역전파이다.
즉 (S1−exp(a1)t1)exp(a1)=y1−t1이 된다.

정리
위의 모든 과정을 하나의 그림으로 요약하면 다음과 같다.

참고












