백준 - 잘못 구현한 에라토스테네스의 체 (15897번)

백준 - 잘못 구현한 에라토스테네스의 체 (15897번)

에라토테네스의 체는 소수를 구할 때 쓰이는 방법이다.

말로 설명을 듣는 것보다 위 링크의 그림을 보면 바로 이해가 된다.
간략하게 요약하면 n까지의 소수를 구할 때 1<= x <=$sqrt(n)$ 까지의 x들의 배수들을 모두 지우고 남은 숫자들이 소수가 된다는 것이다.

사실 이 문제는 에라토스테네스의 체와는 상관이 없다. 그냥 설명해봤다.

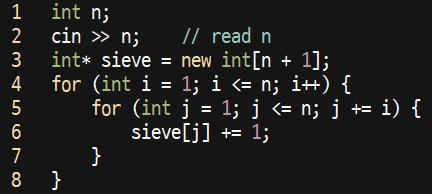
오히려 이 문제는 조화수열문제인데, 위 코드의 식에서 조화수열의 규칙이 발견되기 때문이다.

n을 12라 가정하면
i = 1 -> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 (12개)
i = 2 -> 1, 3, 5, 7, 9, 11 (6개)
i = 3 -> 1, 4, 7, 10 (4개)
i = 4 -> 1, 5, 9 (3개)
i = 5 -> 1, 6, 11 (3개)
i = 6 -> 1, 7 (2개)
i = 7 -> 1, 8 (2개)
i = 8 -> 1, 9 (2개)
i = 9 -> 1, 10 (2개)
i = 10 -> 1, 11 (2개)
i = 11 -> 1, 12 (2개)
i = 12 -> 1 (1개)

i가 1, n일 때는 그 값이 항상 일정할테니 결과 값에 n+1을 더해주고, 다른 연산은 생략할 수 있다.
단 주어진 n이 1일 때는 n+1이 아니라 1만 더해줘야 한다.

조화수열의 핵심은 같은 값을 가지는 구간을 구하는 것인데, i마다 어느 값을 가지는지를 찾는지 생각해보면,

각 i마다 가지는 값은 1 + (n-1) / i 이라는 것을 알 수 있다. (끄적이다 얻어걸렸다 증명은 못하겠다)
조화수열도 사실 이걸 가지고 끄적이다 얻어걸렸는데, 조화수열이 보통 $n / (n / i)$의 수식이기 때문에 n대신 n-1을 넣어보니 딱 맞아떨어졌다(분모의 소숫점은 버려짐).
예를 들어,
n = 12, i = 4를 넣어서 테스트해보면 1 + (11) / 4 = 4이고, (11) / (11 / 4) = 5가 된다.
즉 4~5는 3의 값을 가진다.
i = 5는 생략할 수 있으므로, i = 6을 구해보면
1 + (11) / 6 = 2, (11) / (11 / 6) = 11이 된다.
즉 6~11은 1의 값을 가진다.

#include <cstdio>
#include <iostream>
#include <algorithm>

using namespace std;

unsigned long long n;

int main(void)
{
	cin >> n;
	unsigned long long ans = n;
	for (unsigned long long i = 2, j = 0; i < n; i = j + 1) {
		j = (n - 1) / ((n - 1) / i);
		unsigned long long num = 1 + (n - 1) / i;
		ans += (j - i + 1) * num;
	}
	if(n != 1)
		ans++;
	cout << ans << "\n";
	return 0;
}