17484.진우의 달 여행 (Small) : https://www.acmicpc.net/problem/17484
문제 설명
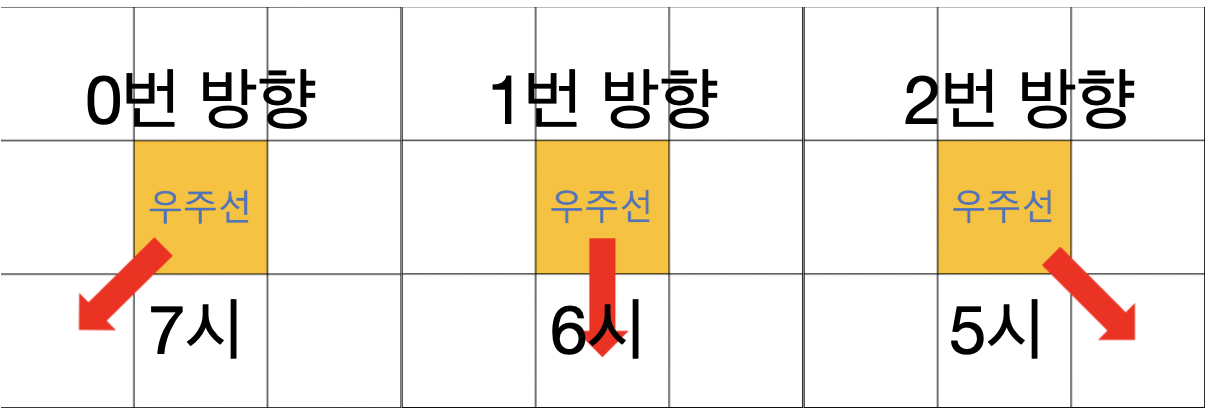
지구에서 달까지 가기 위해 최소한의 연료를 사용해야한다. 7시, 6시, 5시 총 3방향으로 이동할 수 있으며 직전에 움직인 방향과 같은 방향으로는 갈 수 없다. (6시 -> 6시 (X), 5시 -> 6시 (O))
최소한의 연료로 달에 도착했을 때, 이 때 연료의 양은 얼마인가?
문제 접근
문제를 읽자마자 DP구나 싶었다. Bottom-Up으로 목적지까지 최적해를 구하는 방식으로 문제를 풀어야 겠구나 싶었다. 값의 범위가 작아 dfs로도 가능할 듯 싶다.
이전에는 3차원배열을 사용하는게 꺼려졌었다. 3차원은 종이에 끄적이기에도 직관적으로 이해가 되지 않을 뿐더러 값을 다루기가 쉽지 않았다. 하지만 이 문제같이 직전의 방향을 메모제이션을 해야할 경우에는 오히려 사용하는게 좋다.
Dynamic Programming
int[][][] dp = new int dp[n][m][3]; // d번 방향으로부터 온 점 (n, m)이라 하자.1. 0열인 경우 // (0, 0)으로 시작하는게 쉬우므로 0열부터 시작한다고 가정
현재 위치가 1행 0열 인경우 이 점은 0번 방향 또는 1번 방향으로부터 왔을 것이다. 2번 방향(5시)에서 올 수 없다. (-1열은 없기 때문)
그럼 0행 0열은 어느 방향에서 와야할까?
1번 방향(6시)만 아니면 된다. 그럼 남은건 0번 방향과 2번 방향인데, 0행 0열은 2번 방향(5시)에서 올 수가 없으므로 무조건 0번 방향에서 와야한다.
그럼 0행 1열은 어느 방향에서 와야할까?
1행 0열이 0번 방향에서 왔으므로 중복되는 0번 방향을 제외한 2번 또는 1번 방향 둘 중 최솟값으로 하면 된다.
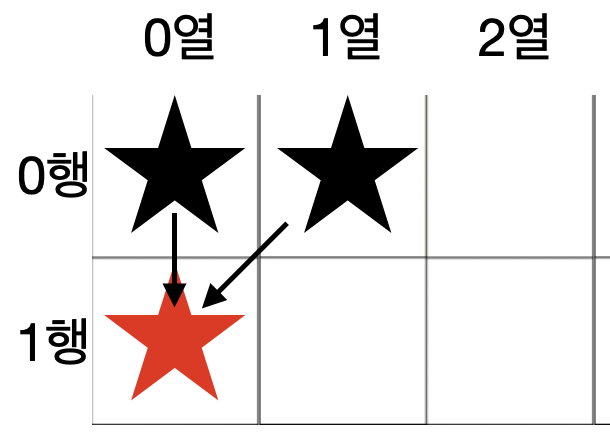
위와 같은 그림일 것이다. 코드로 나타내보자.
if(c == 0) {
// (r, c) 점이 1번 방향으로 부터 왔을 때,
dp[r][c][1] = dp[r - 1][c][0] + board[r][c];
// (r, c) 점이 0번 방향으로 부터 왔을 때, 직전 방향은 1번과 2번 방향 둘 다 가능
dp[r][c][0] = Math.min(dp[r - 1][c + 1][1] dp[r - 1][c + 1][2]) + board[r][c];2. m - 1 열인 경우
현재 위치가 1행 3열 인경우 이 점은 2번 방향 또는 1번 방향으로부터 왔을 것이다. 0번 방향(7시)에서 올 수 없다. (마지막열은 3열이기 때문)
그럼 0행 2열은 어느 방향에서 와야할까?
1행 3열이 2번 방향에서 왔으므로 중복되는 2번 방향을 제외한 0번 또는 1번 방향 둘 중 최솟값으로 하면 된다.
그럼 0행 3열은 어느 방향에서 와야할까?
1번 방향(6시)만 아니면 된다. 그럼 남은건 0번 방향과 2번 방향인데, 0행 3열은 0번 방향(7시)에서 올 수가 없으므로 무조건 2번 방향에서 와야한다.
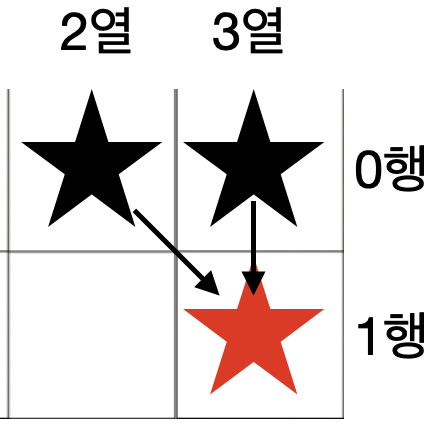
위와 같은 그림일 것이다. 코드로 나타내보자.
if(c == m - 1) {
// (r, c) 점이 1번 방향으로 부터 왔을 때,
dp[r][c][1] = dp[r - 1][c][2] + board[r][c];
// (r, c) 점이 2번 방향으로 부터 왔을 때, 직전 방향은 0번과 1번 방향 둘 다 가능
dp[r][c][0] = Math.min(dp[r - 1][c - 1][0] dp[r - 1][c - 1][1]) + board[r][c];3. 그 외의 경우
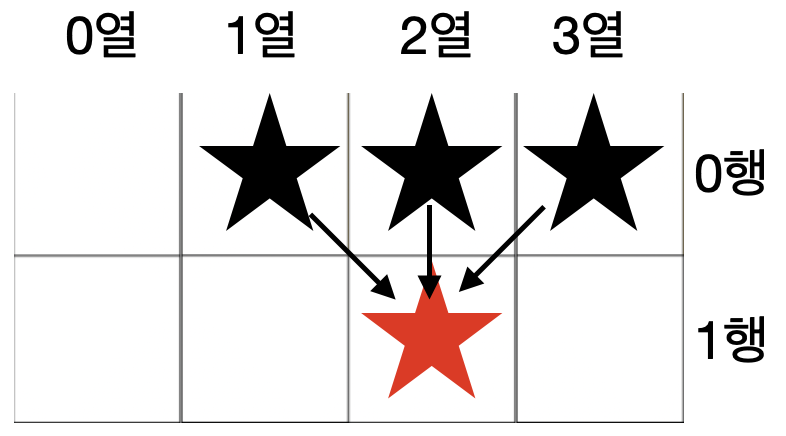빨간색 별이 위치한 1행 2열은 어떤 방향에서든 올 수 있다.
0행 1열 별은 2번 방향이 아니기만 하면 되고,
0행 2열 별은 1번 방향이 아니기만 하면 되고,
0행 3열 별은 0번 방향이 아니기만 하면 된다.
else {
dp[r][c][0] = Math.min(dp[r - 1][c + 1][1], dp[r - 1][c + 1][2]) + board[r][c];
dp[r][c][1] = Math.min(dp[r - 1][c][0], dp[r - 1][c][2]) + board[r][c];
dp[r][c][2] = Math.min(dp[r - 1][c - 1][1], dp[r - 1][c - 1][0]) + board[r][c];
}우리가 구해야할 값은 최소한의 연료량이므로, 초기 dp값만 설정해주고 나머지는 INF로 초기화해주자.
전체 코드 (dp)
package enterprise.sw_category;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
public class BOJ17484_1 {
static int n, m;
static int[][] board;
static int[][][] dp;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] s = br.readLine().split(" ");
n = Integer.parseInt(s[0]);
m = Integer.parseInt(s[1]);
board = new int[n][m];
dp = new int[n][m][3];
for(int i = 0; i < n; i++) {
s = br.readLine().split(" ");
for(int j = 0; j < m; j++) {
board[i][j] = Integer.parseInt(s[j]);
Arrays.fill(dp[i][j], (int)1e9);
}
}
for(int j = 0; j < m; j++) {
dp[0][j][0] = board[0][j];
dp[0][j][1] = board[0][j];
dp[0][j][2] = board[0][j];
}
for(int i = 1; i < n; i++) {
for(int j = 0; j < m; j++) {
if(j == 0) {
dp[i][j][0] = Math.min(dp[i - 1][j + 1][1], dp[i - 1][j + 1][2]) + board[i][j];
dp[i][j][1] = dp[i - 1][j][0] + board[i][j];
} else if(j == m - 1) {
dp[i][j][2] = Math.min(dp[i - 1][j - 1][1], dp[i - 1][j - 1][0]) + board[i][j];
dp[i][j][1] = dp[i - 1][j][2] + board[i][j];
} else {
dp[i][j][0] = Math.min(dp[i - 1][j + 1][1], dp[i - 1][j + 1][2]) + board[i][j];
dp[i][j][1] = Math.min(dp[i - 1][j][0], dp[i - 1][j][2]) + board[i][j];
dp[i][j][2] = Math.min(dp[i - 1][j - 1][1], dp[i - 1][j - 1][0]) + board[i][j];
}
}
}
int min = (int)1e9;
for(int j = 0; j < m; j++) {
for (int i = 0; i < 3; i++) {
min = Math.min(min, dp[n - 1][j][i]);
}
}
System.out.println(min);
}
}
DFS
사실 이문제는 dfs로도 가능하다. 방향이 3개이며, 2 <= n, m <= 6이다. 즉 시간복잡도는 O(3^m * n)으로 판단하였을 때 제한시간 1초 안에 실행된다.
DFS 로직은 간단하다. n행에 도달했을 때 재귀를 종료하여 전역변수로 선언한 static int res = (int)1e9의 최솟값 res를 구해주면 된다. 단, 0열 ~ m-1열까지 for문을 돌려 모든 출발점부터 전체 경로를 탐색해야 한다.
전체 코드 (dfs)
package enterprise.sw_category;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
public class BOJ17484 {
static int n, m;
static int[][] board;
static int[][][] dp;
static int[] dx = {-1, 0, 1};
static int res = (int)1e9;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] s = br.readLine().split(" ");
n = Integer.parseInt(s[0]);
m = Integer.parseInt(s[1]);
board = new int[n][m];
dp = new int[n][m][3];
for(int i = 0; i < n; i++) {
s = br.readLine().split(" ");
for(int j = 0; j < m; j++) {
Arrays.fill(dp[i][j], -1);
board[i][j] = Integer.parseInt(s[j]);
}
}
// int res = (int)1e9;
for(int i = 0; i < m; i++) {
goToMoon(0, i, -1, 0);
}
System.out.println(res);
}
static void goToMoon(int r, int c, int dir, int sum) {
if(r == n) {
res = Math.min(res, sum);
return;
}
for(int i = 0; i < 3; i++) {
if(dir == i) continue;
int nx = c + dx[i];
if(nx >= 0 && nx < m) {
goToMoon(r + 1, nx, i, sum + board[r][c]);
}
}
}
}
