강한 연결 요소 (Strongly Connected Component)
방향성이 존재하는 유향 그래프에서 그룹 내의 모든 정점이 다른 모든 정점들에 대하여 방문할 수 있는 경우에 그 그룹이 강하게 연결되었다고 하고, 이것을 강한 연결 요소 혹은 강한 결합 요소라고 말합니다. 또한 그래프의 부분 그래프의 정점들도 강한 연결 요소가 될 수 있습니다. 강한 연결 요소가 성립하는 그래프는 반드시 하나의 유향 사이클을 포함하는 그래프입니다.
알고리즘 원리
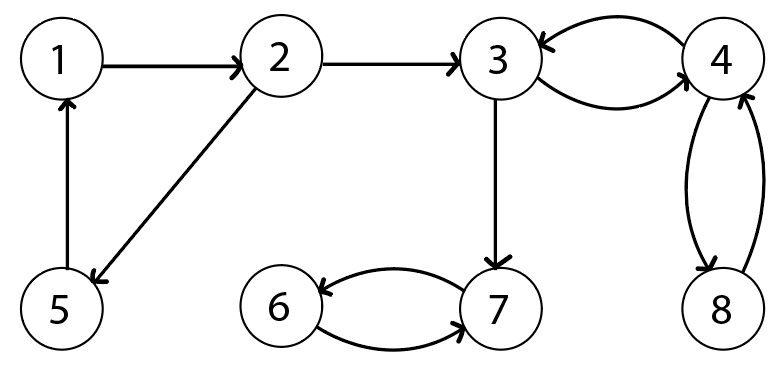
깊이 우선 탐색(DFS)을 기반으로 하는 선형 탐색 알고리즘을 사용할 수 있습니다. 코사라주의 알고리즘과 타잔의 알고리즘이 있으며 그 중 알고리즘 적용이 쉬운 타잔의 알고리즘을 통해 위 그래프에서 강한 연결 요소(SCC)를 찾아보겠습니다. 타잔의 알고리즘은 한번의 DFS로 스택을 사용해 SCC를 추출하는 알고리즘입니다.
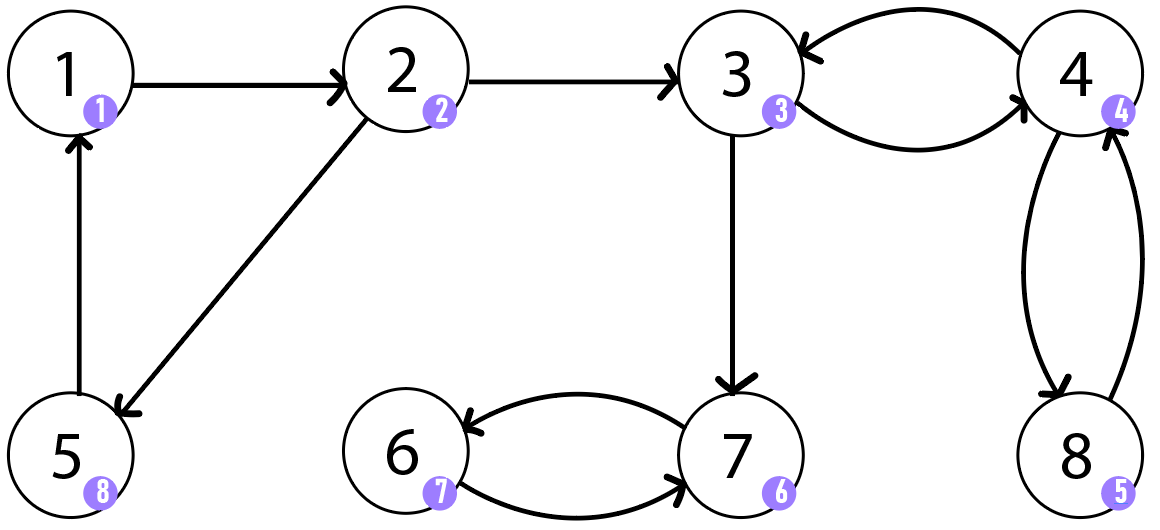
기본적으로 위 그래프의 DFS 수행 순서는 사전 순에 따라 1 -> 2 -> 3 -> 4 -> 8 -> 7 -> 6 -> 5 가 될 것이며 방문할 때마다 해당 정점을 스택에 삽입합니다.
SCC의 발견 조건은 자신의 자식 정점들이 자신의 부모 정점으로 갈 수 있는 경우가 없는 경우이다
자신을 포함한 하나의 SCC가 발견되고 스택에서 자신과 자신보다 위에 쌓여있는 정점들을 뽑아서 하나의 SCC를 성립합니다.
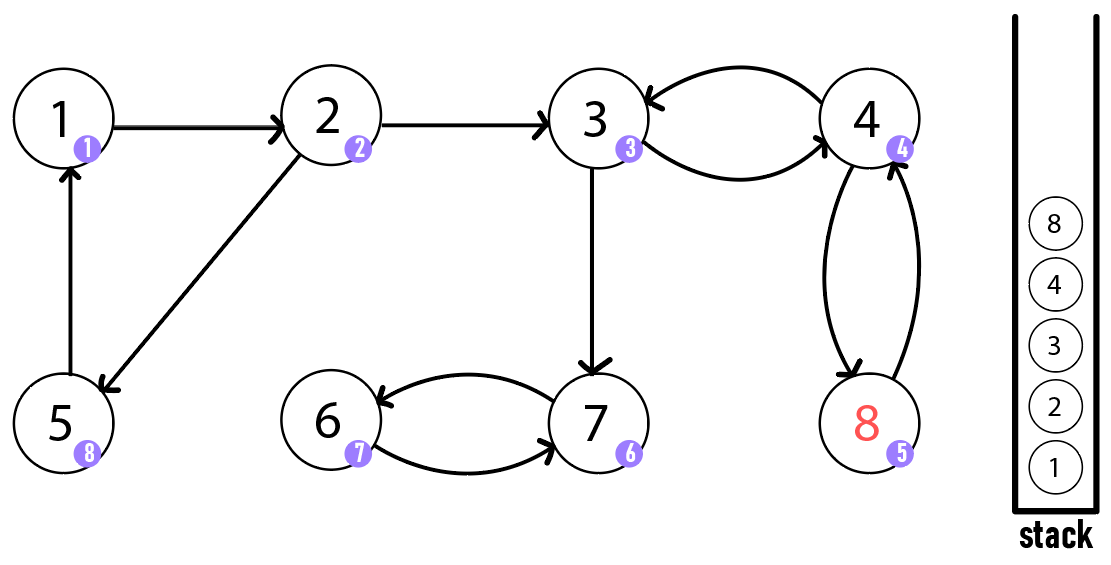
우선 정점을 방문합니다. 방향 간선대로 1, 2, 3, 4, 8을 방문하고 스택에 삽입합니다. 정점 8은 방문할 수 있는 정점이 정점 4인데 자신의 부모 정점이므로 SCC의 발견 조건에 맞지 않아 종료합니다.
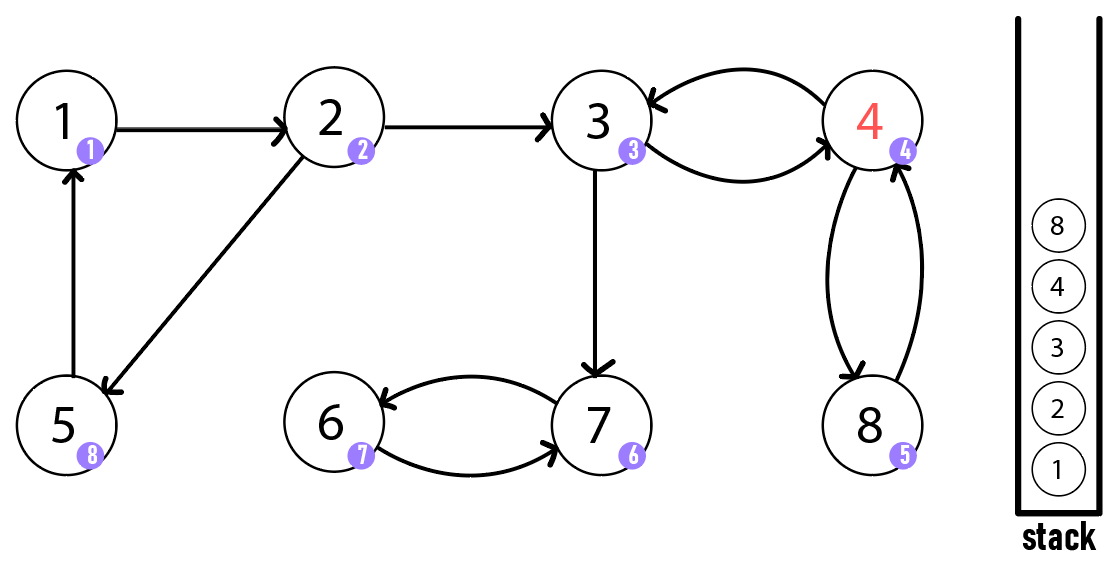
정점 4도 마찬가지로 자신의 부모 정점인 정점 3으로 갈 수 있으므로 조건에 맞지 않아 종료합니다.
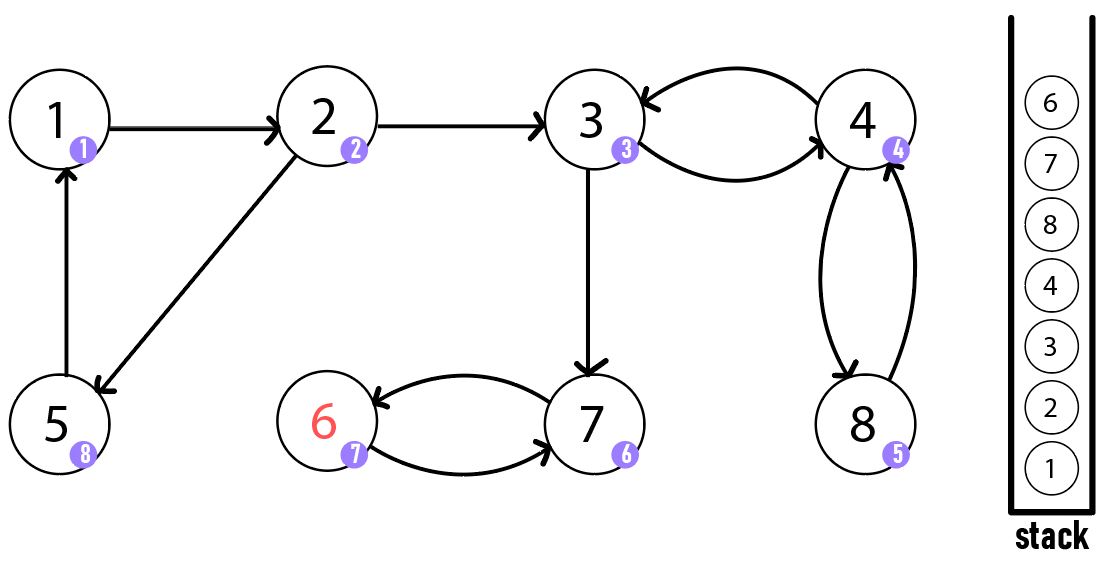
그 다음 정점 3은 정점 7로 방문할 수 있습니다. 정점 7을 방문하고 스택에 삽입합니다. 다시 정점 7은 정점 6을 방문하여 스택에 삽입합니다. 정점 6은 자신의 부모 정점 7로 갈 수 있으므로 조건에 맞지 않아 종료합니다.

정점 7로 돌아갔고 정점 7은 돌아갈 수 있는 부모 정점이 없으므로 SCC 발견 조건을 만족합니다. 정점 7과 자신의 자식 정점인 정점 6도 마찬가지로 정점 7의 부모 정점으로 돌아갈 수 없습니다. 그러므로 SCC를 추출하게 됩니다. 스택에서 정점 7과 그 위에 쌓여있는 정점 6을 묶어서 하나의 SCC를 성립합니다.
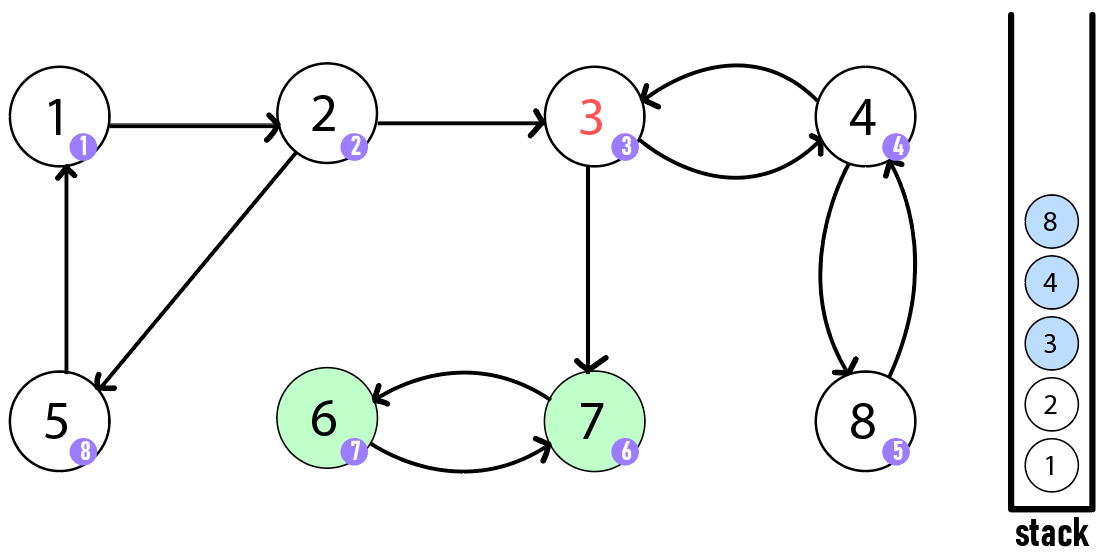
이제 정점 3으로 돌아갔을 때 정점 3은 더이상 방문할 수 있는 정점이 없으므로 SCC 발견 조건을 만족합니다. 그러므로 스택에서 정점 3과 그 위에 쌓여있는 정점 4와 8을 묶어서 하나의 SCC를 성립합니다. 정점 7도 정점 3의 자식 정점이지만 이미 다른 SCC로 추출되어 스택에서 빠져나갔기 때문에 정점 3과는 다른 SCC로 각각 속하게 되는 것입니다.
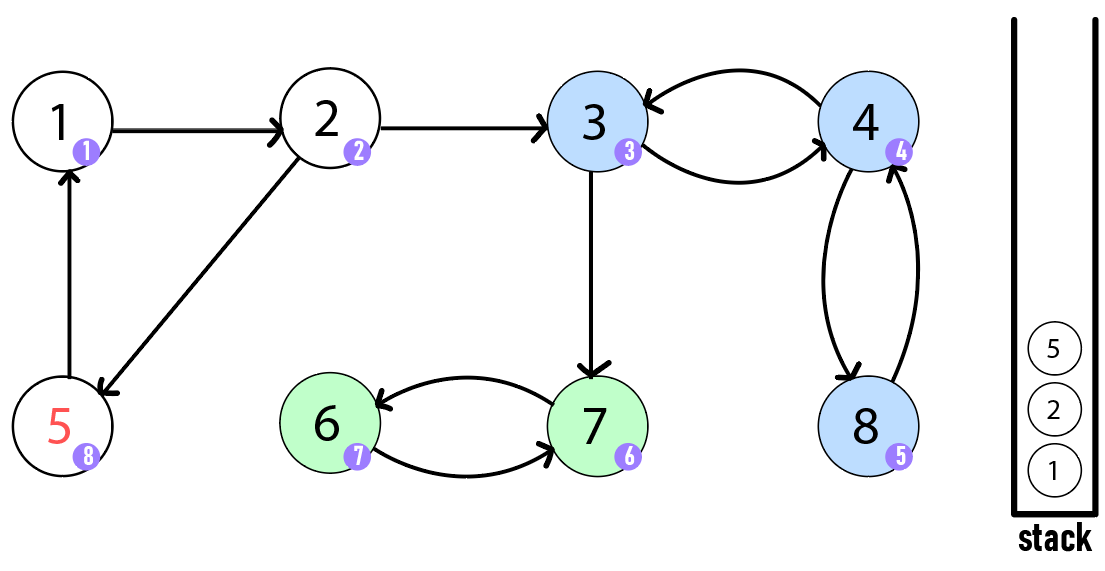
정점 2로 돌아가서 정점 2는 아직 방문하지 않은 정점 5를 방문합니다. 정점 5는 부모 정점 1로 갈 수 있으므로 종료합니다.
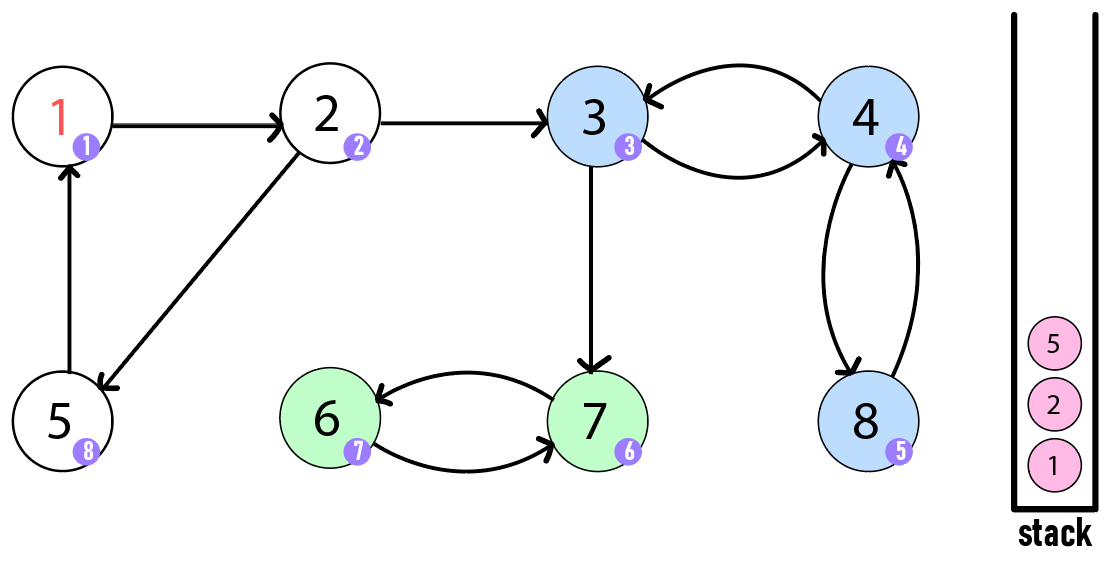
정점 1로 갔을 때 정점 1은 자신이 루트 정점이었으므로 돌아갈 부모 정점이 없어 SCC 발견 조건을 만족합니다. 자기 자신인 정점 1을 포함하여 그 위에 쌓인 정점 2와 정점 5가 하나의 SCC로 성립합니다.
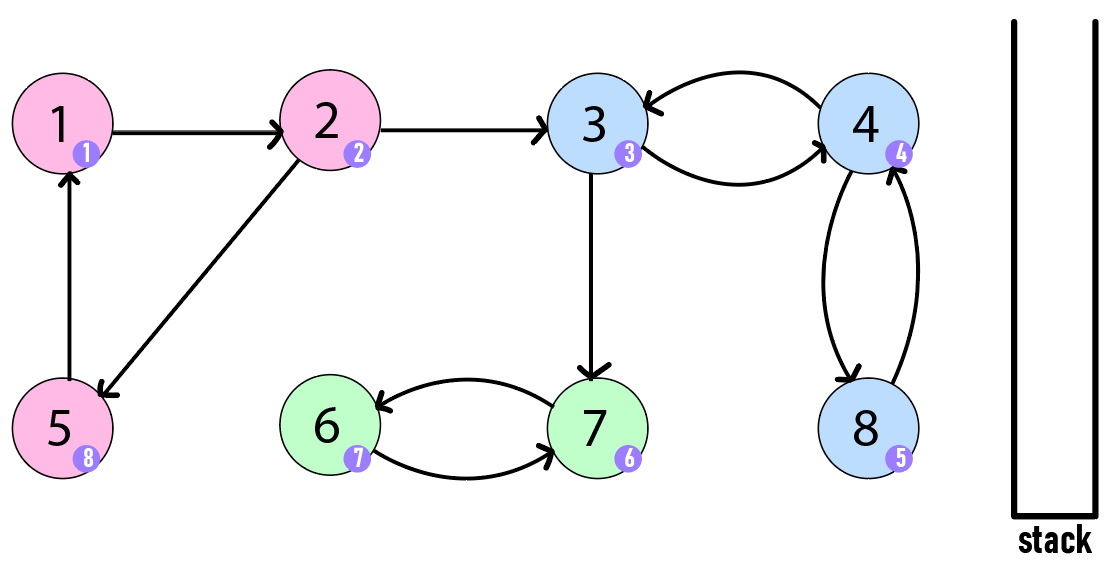
모든 SCC를 발견하여 스택이 비었고 결과적으로 [정점 6, 7], [정점 3, 4, 8], [정점 1, 2, 5]가 강한 연결 요소가 됩니다.
알고리즘 구현
// Algorithm Analysis
// 강한 연결 요소 (Strongly Connected Component)
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.Arrays;
import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
import java.util.*;
public class Main {
static int MAX = 10001;
static int v, e, id;
static int[] d = new int[MAX];
static int sccNum; // scc 개수
static int[] sn = new int[MAX]; // i가 속한 SCC의 번호
static List<List<Integer>> a = new ArrayList<>();
static boolean[] finished = new boolean[MAX]; // SCC 성립되면 true
static Stack<Integer> s = new Stack<>();
static List<List<Integer>> SCC = new ArrayList<>();
public static void main(String[] args) throws Exception {
// 그래프 정보 입력
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
StringBuilder sb = new StringBuilder();
int n = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
for(int i = 0; i<MAX; i++){
List<Integer> list = new ArrayList<>();
a.add(list);
}
for(int i = 0; i<c; i++){
st = new StringTokenizer(br.readLine());
int x = Integer.parseInt(st.nextToken());
int y = Integer.parseInt(st.nextToken());
a.get(x).add(y);
}
// DFS를 수행하며 SCC 추출
for (int i = 1; i <= n; i++) {
if (d[i] == 0) DFS(i);
}
//sccNum = SCC 개수
System.out.println("SCC 개수 : "+sccNum);
// System.out.println(SCC);
// 각 SCC 출력
for (List<Integer> currSCC : SCC) {
for (int curr : currSCC){
System.out.print(curr+" ");
}
System.out.println();
}
}
public static int DFS(int c){
d[c] = ++id;
s.push(c);
int result = d[c];
Iterator<Integer> itr = a.get(c).iterator();
while(itr.hasNext()){
int next = itr.next();
//처음 방문하는 정점
if(d[next] == 0) result = Math.min(result, DFS(next));
//방문은 했었지만 SCC 성립 전인 정점
else if(!finished[next]) result = Math.min(result, d[next]);
}
if(result == d[c]){
List<Integer> scc = new ArrayList<>();
while(true){
int t = s.pop();
scc.add(t);
finished[t] = true;
sn[t] = sccNum;
if(t == c) break;
}
SCC.add(scc);
// System.out.println(scc);
sccNum++;
}
return result;
}
}
/* 결과 출력
SCC 개수 : 3
6 7
3 4 8
1 2 5
*/
/* 입력 그래프 정보
8 14
1 2
2 3
2 5
2 6
3 4
3 7
4 3
4 8
5 1
5 6
6 7
7 6
8 4
8 7
*/시간 복잡도 : O(V + E)
강한 연결 요소의 시간 복잡도는 정점 수 + 간선 수입니다.
