Deep Reinforcement learning: A Survey

Seon·2025년 1월 8일
DRLRL강화학습
0

알고리즘

목록 보기
3/3

https://ieeexplore.ieee.org/abstract/document/9904958

Abstract

Deep Reinforcement Learning(DRL)은 Deep Learning(DL)에서 데이터의 특징을 자동으로 추출하고, 추출한 특징을 Reinforcement Learning(RL)에 적용해 최적의 행동을 학습하는 방식이다. 즉, 전처리 단계 없이 자동으로 특징 학습과 강화 학습을 수행하여 end-to-end 학습 제어가 가능하다.

하지만 DRL의 이론과 응용 분야에 존재하는 문제점: 제한된 샘플, 희소한 보상, 다중 에이전트

문제가 되는 경우문제점
제한된 샘플데이터의 특징을 잘 뽑아낼 수 없는 문제
희소한 보상보상에 대한 명확성이 떨어지는 문제
여러 에이전트각 에이전트들의 행동이 다른 에이전트들에게도 영향을 주어 복잡해지는 문제

이 논문에서는 DRL의 기본 이론, 핵심 알고리즘 및 주요 연구 도메인에 대한 포괄적인 개요를 제공한다.

INTRODUCTION

RL의 목표는 에이전트의 행동 방법을 학습하여 예상되는 장기 보상을 극대화하는 것이었다. 초기 RL은 특성 표현 능력이 부족하여 차원이 낮은 상태 및 동작 공간에 있는 작업만 해결할 수 있었다. 하지만 현실은 고차원 상태와 연속적인 동작 공간을 가져 RL의 적용이 제한되는 경우가 많았다. 이 문제를 해결하기 위해 고차원 추상 입력에서 특징을 추출하여 강력한 표현 기능을 가지고 있는 DL과 RL이 결합되어 새로운 연구 분야에 활용이 되었다.

이 논문의 세 가지 측면은 다음과 같다.

  1. 학습 목표에 따라 DRL 알고리즘을 세 가지 범주로 분류하고 각 방법 클래스 간의 관계를 명확히 보여준다.(Value-Based, Policy-Based, Maiximum Enropy Based 알고리즘)
  2. 다양한 코드 기반에서 구현된 일반적으로 사용되는 DRL 알고리즘을 자세히 분석한다.
  3. 기존 RL 및 DRL의 다양한 과제를 해결하는 데 초점을 맞춘 추가 연구 주제를 분석하고 논의한다.

BACKGROUND

RL을 해결하기 위한 마르코프 결정 프로세스(MDP), 동적 프로그래밍(DP), 몬테카를로(MC), 시간적 차이(TD) 방법을 기반으로 하는 알고리즘이 포함된다.

마르코프 결정 프로세스(Markov Decison process, MDP)

MDP는 순차적 의사 결정 문제를 해결하기 위한 고전적인 프레임워크로 다음과 같은 가정에서 진행된다.

  1. 환경은 마르코프적이므로 다음 시간 단계의 상태는 이전 상태와 무관하게 현재 상태에 의해서만 결정된다.
    P(st+1∣st,st−1,⋯ ,s0)=P(st+1∣st)P(s_{t+1}|s_t,s_{t-1},\cdots,s_0)=P(s_{t+1}|s_t)
  2. 에이전트는 언제든지 모든 환경 정보를 관찰할 수 있다.
    하지만 위 가정이 항상 적절하지 않아 부분적으로 관찰 가능한 MDP와 같은 다양한 MDP 변형이 제안되었다.

RL의 목표는 누적 보상을 최대화하는 궤적을 찾는 것이다. 누적 보상 GtG_t는 시간 t에서 시작하여 모든 미래 보상의 합으로 표현된다.

Gt=Rt+1+γRt+2+γ2Rt+3+⋯=∑k=0∞γkRt+k+1G_t=R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+\cdots=\sum_{k=0}^\infty\gamma^kR_{t+k+1}

여기서, RiR_i는 시간 i에서 얻는 보상이고, γk\gamma^k는 시간에 따른 할인율로 미래 보상은 시간이 지남에 따라 줄어들도록 만들어 준다.

벨만 방정식(Bellman Equations)

상태 전이 확률과 정책이 존재하기 때문에, 특정 상태의 반환을 계산하는 것은 간단하지 않다. 상태에서 시작하여 모든 궤적의 반환을 계산하고, 그것들의 기대값을 구해야 한다.

상태 가치 함수 V(s)

상태 가치 함수는 상태 s에서의 기대 반환을 정의하는 함수로 다음과 같이 나타낼 수 있다.

V(s)=Es,a∼τ[∑k=0∞γkRt+k+1]V(s)=\mathbb{E}_{s,a\sim\tau}[\sum_{k=0}^\infty\gamma^kR_{t+k+1}]

이를 확장하면

V(s)=∑(s,a,… )∼τπ(at∣st)p(st+1∣st,at)∑k=0∞γkRt+k+1V(s)=\sum_{(s,a,\dots)\sim\tau}\pi(a_t|s_t)p(s_{t+1}|s_t,a_t)\sum_{k=0}^\infty\gamma^kR_{t+k+1}

재귀적으로 표현하면

V(s)=Eπ[Rt+1+γV(st+1)∣st=s]V(s)=E_\pi[R_{t+1}+\gamma V(s_{t+1})|s_t=s]

이때 τ\tau는 상호작용 궤적, π(at∣st)\pi(a_t|s_t)는 정책 함수, p(st+1∣st,at)p(s_{t+1}|s_t,a_t)는 상태 전이 확률이다.

상태-행동 가치 함수 Q(s,a)

상태-행동 가치 함수는 상태 s에서 행동 a를 수행했을 때의 기대 반환을 정의하는 함수로 다음과 같이 나타낼 수 있다.

Q(s,a)=Eπ[Rt+1+γQ(st+1,at+1∣st=s,at=a]Q(s,a)=\mathbb{E}_\pi[R_{t+1}+\gamma Q(s_{t+1},a_{t+1}|s_t=s,a_t=a]

위 두 수식은 벨만 방정식이라 불리며 강화학습 문제를 해결하는 기본 방정식이다. 그리고 수식에서 보이듯 벨만 방정식은 발생 확률에 따라 모든 궤적의 누적 보상의 가중 평균을 계산한다.

최적 정책 및 최적 가치 함수

최적 상태 가치 함수 V∗(s)V^*(s): 모든 상태에서 가장 큰 값을 가지는 가치 함수
최적 상태-행동 가치 함수 Q∗(s,a)Q^*(s,a): 모든 상태와 행동에서 가장 큰 값을 갖는 가치 함수
최적 정책 π(a∣s)\pi(a|s): 최적 상태-행동 가치 함수 Q∗(s,a)Q^*(s,a)를 최대화하는 정책

On-Policy & Off-Policy Methods

On-Policy와 Off-Policy는 강화 학습에서 데이터를 학습하는 두 가지 다른 방식으로, 주요 차이는 행동 정책(Behavior Policy)와 목표 정책(Target Policy)이 동일한지의 여부이다.

  • 행동 정책: 환경과 상호작용하여 학습 데이터를 생성하는 데 사용되는 정책
  • 목표 정책: 에이전트가 학습해야 하는 정책

On-Policy 방법에선 목표 정책을 직접 사용하여 다음 단계의 정책 최적화를 위한 데이터를 생성한다. 이 과정에서 생성된 데이터는 정책 최적화가 끝나면 폐기된다. 따라서 행동 정책과 목표 정책이 동일하다.

Off-Policy 방법에선 행동 정책을 사용해 환경과 상호작용하며 생성된 샘플을 버퍼에 저장한다. 학습 과정에서는 이 버퍼에서 샘플을 가져와 목표 정책을 업데이트한다. 이 경우 학습 데이터가 이전의 행동 정책에서 생성된 것이라 행동 정책과 목표 정책이 동일하지 않을 수 있다.

On-Policy는 정책을 직접적으로 최적화할 수 있다는 장점이 있고, Off-Policy는 데이터의 효율성이 높다는 장점이 있다.

동적 프로그래밍 기법(Dynamic Programming, DP)

환경 모델이 완전히 알려져 있는 경우, 벨만 방정식은 동적 프로그래밍 방법을 통해 해결할 수 있다. 동적 프로그래밍 기반 알고리즘은 주로 정책 반복과 가치 반복으로 나뉜다.

정책 반복

정책 평가와 정책 개선 단계를 반복하여 최적 정책에 수렴하는 방식

  • 정책 평가 단계: 현재 정책을 사용하여 가치를 계산한다.
  • 정책 개선 단계: 이전 단계에서 계산된 가치를 사용하여 더 나은 정책을 생성한다.

가치 반복

각 상태에서 모든 행동을 차례로 수행하며 Q-value를 계산하는 것으로 최적의 Q-value은 현재 상태의 가치로 사용되며, 각 상태의 최적 값이 더 이상 변하지 않을 때 반복이 종료된다.

정책 반복의 정책 평가 단계는 가치 함수가 수렴해야 하지만, 가치 반복에서는 최적의 가치와 최적의 정책이 수렴한다. 따라서 가치 함수가 최적 값에 도달하면, 정책도 수렴하므로 반복 단계를 단순화할 수 있다.

몬테 카를로 기법(Monte Carlo, MC)

주로 환경의 일부 속성은 얻기가 어려워 환경을 완전히 모델링하는 것이 거의 불가능하다. 이 경우, MC 방법을 사용하여 가치를 평가할 수 있다. 특정 상태의 가치를 평가하는 MC 방법의 단계는 다음과 같다.

  1. 해당 상태에서 여러 번 시뮬레이션을 실행해 여러 경로를 얻는다.
  2. 각 경로의 누적 보상을 계산한다.
  3. 다음 수식을 사용하여 이 상태의 가치를 계산한다.
    V(st)=V(st)+α(Gt−V(st))V(s_t)=V(s_t)+\alpha(G_t-V(s_t))

V(st)V(s_t)는 상태 sts_t의 추정 가치, G_t는 각 경로에서의 누적 보상

추정 가치를 업데이트하기 위한 보상은 실제 상호작용 경로에서 얻어지므로, 추정 가치는 편향되지 않는다.

시간차 방법(Temporal Difference, TD)

TD 방법은 MC 방법과 유사하게 경험으로부터 직접 학습하며, 환경의 동적 모델을 알 필요가 없다. 그러나 TD 방법과 MC 방법의 차이는 현재 상태에서 터미널 상태까지 진행하는 대신 한 단계만 시뮬레이션한다는 것이다.

가장 간단한 TD 방법인 TD(0)의 갱신 식은 다음과 같다.

V(st)=V(st)+α(Rt+1+γV(st+1)−V(st))V(s_t)=V(s_t)+\alpha(R_{t+1}+\gamma V(s_{t+1})-V(s_t))

여기서, Rt+1+γV(st+1)R_{t+1}+\gamma V(s_{t+1})는 t+1 시점에서의 추정 값으로 TD 목표라고 하며, Rt+1+γV(st+1)−V(st)R_{t+1}+\gamma V(s_{t+1})-V(s_t)는 TD 오차라고 한다.

이를 통해, TD 방법은 불완전한 시퀸스로부터 학습할 수 있음을 알 수 있다. 그리고 에피소드 기반 업데이트를 피하고 수렴 속도를 향상시킬 수 있다. TD(0)의 갱신은 기존의 추정치를 기반으로 이루어지며, 이는 DP와 유사하여 부트스트랩 방식으로 분류된다. TD 오차를 사용해 가치 함수를 업데이트하는 에이전트는 On-Policy 방법(ex. SARSA) 또는 Off-Policy 방법(Q-Learning)으로 훈련될 수 있다.

Off-Policy 방식 중 하나인 Q-Learning은 초기 강화 학습 알고리즘에서 획기적인 발전을 이룬 방법이었다. Q-Learning의 갱신 식은 다음과 같다.

Q(st,at)=Q(st,at)+α(Rt+1+γmax⁡aQ(st+1,a)−Q(st,at))Q(s_t,a_t)=Q(s_t,a_t)+\alpha(R_{t+1}+\gamma\max_aQ(s_{t+1},a)-Q(s_t,a_t))

α∈(0,1]\alpha \in (0,1]은 step size를 나타낸다. 현재 Q-value를 계산할 때, Q-Learning은 상호작용 시퀸스를 따르지 않고 다음 단계에서 가장 큰 Q-value를 갖는 행동을 선택하는데, 이 경우 Q-value의 과대 추정을 초래할 수 있다.

정책 경사법(Policy Gradient Methods)

위에서 논의한 바와 같이, 정책 π:S→A\pi:S\rightarrow A는 상태에서 행동으로의 매핑으로, 상태 s에서 행동 a를 선택할 확률을 나타낸다. 이는 모든 행동에 대한 확률 분포 또는 확률 밀도 함수로 정의되며 다음과 같이 나타낼 수 있다.

πθ(a∣s)=P(a∣s,θ)\pi_\theta(a|s)=P(a|s,\theta) θ\theta는 정책의 매개변수

앞서 설명한 DP, MC, TD 방법 모두 최적 Q-value를 계산한 후, 최적 정책을 구해야하며, 이러한 방법들을 값 기반 방법이라고 한다.

반면, 정책을 직접 최적화할 수 있는 또 다른 방법은 정책 경사법(Policy Gradient Methods)라고 한다.

정책 πθ\pi_\theta의 성능 측정을 기대 수익으로 정의하면 다음과 같다.

J(θ)=Vπθ(s)=Eπθ(s)[∑aQ(s,a)πθ(a∣s)]J(\theta)=V_{\pi_\theta}(s)=E_{\pi_\theta}(s)[\sum_aQ(s,a)\pi_\theta(a|s)]

정책 경사 정리를 사용해 θ\theta에 대해 미분하면 정책 최적화를 위한 식을 얻을 수 있다.

▽θJ(θ)=Eπθ(s)[∑aQ(s,a)▽θπθ(a∣s)]\triangledown_\theta J(\theta)=E_{\pi_\theta}(s)[\sum_aQ(s,a)\triangledown_\theta\pi_\theta(a|s)]

정책 업데이트는 다음과 같다.(α\alpha는 학습률)

θ=θ+α▽θJ\theta=\theta+\alpha\triangledown_\theta J

Reinforce 알고리즘은 전통적인 정책 경사 기반 강화 학습 알고리즘으로, 샘플링된 경로에서 MC 방법을 통해 얻은 누적 수익을 사용해 정책을 업데이트한다. 샘플의 경사의 기대값은 실제 경사의 편향되지 않은 추정치이기 때문이다.

Reinforce 알고리즘의 가장 일반적으로 사용되는 변형은 베이스라인을 포함한 형태이다. 이는 경사를 추정할 때 발생하는 분산을 줄이기 위한 목적으로 다음과 같이 표현된다.

▽θJ(θ)=Eπθ(s)[▽θlog⁡πθ(a∣s)(Q(s,a)−b)]\triangledown_\theta J(\theta)=E_{\pi_\theta}(s)[\triangledown_\theta\log\pi_\theta(a|s)(Q(s,a)-b)]

(b는 행동 a와 독립적인 학습된 상태 가치 함수)

값 기반 방법을 사용해 연속적인 행동 공간을 가진 작업을 해결하려면, 먼저 행동 공간을 이산화해야 한다. 하지만 이산화는 항상 차원의 저주 문제를 겪는다. 게다가, 이산화의 step size가 너무 크면 제어 결과가 매끄럽지 않게 되어서 문제가 발생할 수 있다.

반면, 정책 경사법으로 얻은 최적 정책은 행동에 대한 확률 분포 또는 확률 밀도 함수로 표현되며, 이는 연속적이거나 이산적일 수 있어 위의 단점을 피할 수 있다.

액터-크리틱(Actor-Critic) 방법

액터-크리틱 방법은 정책과 가치 함수를 동시에 학습하는 방법을 의미한다.

액터: 정책을 생성하고, 행동을 선택하며, 환경과 상호작용하는 역할을 담당한다.
크리틱: 각 시간 단계에서 액터의 정책에 대한 가치 함수를 평가한다. 액터의 정책을 평가하기 위해 다양한 척도를 사용할 수 있다.

액터-크리틱 구조는 액터가 행동을 선택하고 환경과 상호작용하며, 크리틱은 액터가 성능을 평가하는 방식으로 작동한다. 이 접근 방식은 정책 평가와 개선을 동시에 수행하며, 두 모듈의 상호작용을 통해 정책의 학습 효율성을 높인다.

딥 러닝(Deep Learning, DL)

DL은 이미지 인식, 텍스트 처리 등 다양한 분야에서 강력한 적합 능력과 고차원 데이터를 처리할 때의 뛰어난 표현 능력을 입증했다.

  • AlexNet(2012): 이미지 인식
  • Word2Vec(2013): NLP
  • GAN(2014): 데이터 생성과 복잡한 신경망 구성
  • ResNet(2015): 인간 수준을 초과한 인식 문제를 해결, 컴퓨터 비전(CV)의 핵심 기술
  • Attention(2015): NLP, 이미지 분류에 성과를 냄
  • Transformer(2017): Self-Attention을 활용해 NLP와 딥러닝 발전에 기여

이렇게 DL은 다층 신경망과 뉴런 기반의 구조에 의해 발전해왔다. DL과 RL의 결합으로 탄생한 심층 강화학습은 신경망의 강력한 표현 능력을 활용해 고차원 입력을 처리하고 값을 근사하거나 정책을 학습함으로써 지나치게 큰 상태 공간과 연속적인 행동 공간을 가진 RL 문제를 해결한다.

DRL은 일반적으로 다음과 같이 간주할 수 있다.

원시 상태의 특징으로 매핑(DL)하고, 특징을 행동으로 매핑(RL)한다.
딥 신경망이 블랙박스로 사용될 수 있기 때문에, DRl은 이 두 과정을 하나로 통합하여 고려할 수 있다.
DRL은 여전히 RL에 중점을 두고 의사결정 문제를 해결하므로, 이후 글에선 DL이 RL과 결합되는 방식을 주로 소개한다.

VALUE-BASED DRL METHODS

가치 기반 방법은 가치 함수를 표현하고 최적의 가치 함수를 찾는 데 중점을 RL 방법의 필수적인 클래스로 Q-Learning 알고리즘은 가장 고전적인 가치 기반 알고리즘이다.

Deep Q-Learning

기존 Q-Learning은 대규모 상태 공간과 액션 공간이 있는 문제엔 적합하지 않은 문제가 있어 이후 DL과 Q-Learning이 결합한 Deep Q Network(DQN)이 제안되었다. 다음은 DQN의 학습 세부 정보를 보여주는 Deep Q-Learning Algorithm 유사코드이다.

1. experience replay buffer D를 초기화 2. Q Network와 Target Network 2개 네트워크의 가중치를 동일한 랜덤 값 $\theta$로 초기화 3. 각 에피소드 실행 시 환경을 초기화하고 초기 상태 $\phi(s_0)$ 전처리된 비디오 게임의 이미지로 사용한다. 4. 각 시간에서는 Q Network의 입력으로 $\phi(s_t)$를 사용하여 각 action에 대한 Q value를 얻는다. 5. $a_t$는 $\epsilon$-greedy 방식으로 선택한다. 6. 상태 $s_t$일때 행동 $a_t$를 했을때의 보상 R과 새로운 상태 $\phi(s_{t+1})$을 관찰한다. 7. D에 $\phi(s_t),a_t,R,Q(s_{t+1})$을 추가한다. 8. D에서 랜덤한 m개의 샘플 $\phi(s_t),a_t,R,Q(s_{t+1})$을 추출한다. 9. 만약 $Φ(s_{t+1})$가 종료 상태라면 보상 R_j를 반환 10. 만약 $Φ(s_{t+1})$가 종료 상태가 아니라면 $y_{nt}=R_j+\gamma\max_aQ^-(\phi(s_{j+1},a;\theta^-)$를 반환 11. 손실 함수 L($\theta$)를 사용하여 경사하강법으로 Q Network를 업데이트한다.

Deep Q Network

Q-Learning을 강화 학습 알고리즘으로 사용하는 경우, 간단한 심층 신경망인 DQN이 이미지를 기반으로 저수준 특징을 추출(Conv)하고, 추가적인 도메인 지식 없이 행동 가치 함수를 근사(FC)하기 위해 사용한다. 출력층의 결과는 각 행동에 대한 Q 값이다.

Deep Q Network 아키텍쳐

DQN의 시간 단계 t에서 근사된 Q값은 다음과 같이 표현된다.
y=R+γmax⁡aQ(st+1,a;θ)y=R+\gamma\max_aQ(s_{t+1},a;\theta)
→θ\rightarrow \theta: DQN의 매개변수로, 근사된 Q value와 실제 Q value 간의 평균 제곱 오차(MSE)를 최소화하여 업데이트한다.

탐험 능력을 향상시키기 위해 DQN은 ϵ\epsilon-greddy 방법을 사용한다.

-> 일정한 확률로 ε로 무작위 행동을 선택한다.
-> 나머지 확률 1-ε로 현재 정책에 기반하여 최적 행동을 선택한다.

위 두 방식은 정책에 약간의 노이즈를 추가하는 것과 동일한 효과를 가짐과 동시에 에이전트가 탐험과 활용 사이의 균형을 잘 유지할 수 있도록 도와준다.

Experience Replay

에이전트가 환경과 상호작용하며 얻은 궤적은 시간 영역에서 약간의 상관 관계를 갖는데, 이로 인해 학습 데이터가 편향될 수 있고, Q value의 추정이 왜곡되어 오차가 커질 가능성이 있다. 이러한 문제를 해결하기 위해 데이터를 버퍼에 저장하고 무작위로 선택하여 학습 샘플 간 상관 관계를 제거하는 것도 좋은 방법이다. 또한 Experience Replay를 통해 DQN은 Off-Policy 방법을 사용할 수 있어 데이터 효율성이 크게 향상된다.

Target Network

인접한 시간 단계의 값들을 계산하게 되면 네트워크의 파라미터(θ\theta) 업데이트로 인해 서로 다른 매개변수를 가진 동일한 네트워크에 의해 계산이 되어 출력의 불안정성과 같은 문제를 초래할 수 있는 문제가 있다. 이 문제를 해결하기 위해, 주 네트워크와 동일한 구조를 가지는 Target Network가 도입되었다.

학습 초기: 두 네트워크는 동일한 매개변수(θ\theta)를 사용한다.
학습 과정 전체
→\rightarrow 주 네트워크는 환경과 상호작용하여 학습 샘플을 수집한다.
→\rightarrow 각 학습 단계에서, 타깃 네트워크로부터 얻은 타겟 값과 주 네트워크로부터 계산된 추정 Q value를 사용하여 주 네트워크를 업데이트한다.
→\rightarrow 일정 단계의 학습이 완료될 때마다, 주 네트워크의 매개변수를 Target Network로 동기화한다.

Target Network의 역할: 일정 시간 동안 타겟 값을 변형하지 않고 유지하여 DQN의 안정성을 향상시키고, 학습 과정에서 발생할 수 있는 불안정한 출력 문제를 완화한다.

근사값: 타겟 네트워크의 도움을 통해, 근사 값은 다음과 같이 표현된다.

y=R+γmax⁡aQ−(st+1,a;θ−)y=R+\gamma\max_aQ^-(s_{t+1},a;\theta^-)

Double DQN

Q-Learning 알고리즘에서 환경적 노이즈, 함수 근사, 비정상성, 또는 기타 어떤 이유로 Q value에는 과대평가 문제가 있었다. 이러한 문제에 대한 해결책이 Double Q-Learning이고, DQN과 결합한 알고리즘은 Double Deep Q Network(DDQN)이라 불린다.

DDQN은 행동 선택과 가치 함수 계산을 두 개의 서로 다른 가치 함수(즉, 두 개의 네트워크)로 분리하는 것을 목표로 한다.

  • 주 네트워크: 최적의 행동을 선택한다.
  • 타겟 네트워크: 가치 함수를 추정한다.

주 네트워크의 매개변수로 \theta로, 타겟 네트워크의 매개변수를 \theta^-로 나타낼 때, DDQN에서 타겟 값을 계산하는 식은 다음과 같다.

yi=Rj+1+γQ(sj+1,arg⁡max⁡aQ(sj+1,a;θ);θ−)y_i=R_{j+1}+\gamma Q(s_{j+1},\arg\max_aQ(s_{j+1},a;\theta);\theta^-)
Q(sj+1,arg⁡max⁡aQ(sj+1,a;θ);θ−)Q(s_{j+1},\arg\max_aQ(s_{j+1},a;\theta);\theta^-): 타겟 네트워크를 사용하여 계산된 가치 함수)

두 네트워크의 파라미터 업데이트 방식은 DQN에서와 동일하다.

Prioritized Experience Replay

Experience Replay에서 전이를 샘플링할 때, 각 전이는 동일한 확률로 선택되나 실제 각 전이는 TD 오차가 다르기 때문에 DQN의 역전파에 미치는 영향이 다르다. TD 오차의 절댓값이 클수록 역전파에 미치는 영향이 커진다. 또한, 버퍼의 크기가 제한적이라 학습에 유용한 데이터가 샘플링되기 전 버퍼에서 삭제될 수 있다.

이 문제를 해결하기 위해 등장한 것이 우선순위 경험 재생(Prioritized Experience Replay)이다. 우선순위 경험 재생은 각 전이의 TD 오차를 기준으로 우선순위를 평가한다. TD 오차의 형태는 다음과 같다.

δt=Rt+γmax⁡aQ(st,a)−Q(st−1,at−1)\delta_t=R_t+\gamma\max_aQ(s_t,a)-Q(s_{t-1},a_{t-1})

δtδ_t의 절댓값이 클수록 해당 전이가 선택될 확률이 높아지며, 이는 정책 개선에 더 큰 기여를 한다. 샘플링 과정에서 확률적 우선순위와 중요도 샘플링 방법을 채택했다. 확률적 우선순위는 전이를 최대한 활용할 수 있게하며, 다양성을 보장한다. 중요도 샘플링은 파라미터 업데이트 속도를 늦추고 학습의 안정성을 보장한다.

TD 오차 δt\delta_t는 현재 상태에서의 보상과 현재 상태에서의 최대 Q value의 합에서 이전 Q value의 차이로 정의된다. 이 값이 커질수록 해당 전이는 샘플링이 될 확률이 높아지며, 학습에 더 큰 영향을 미친다.

Dueling Architecture

Dueling Architecture는 Advantage Updating 알고리즘의 아이디어를 채택하여, 이점 함수를 다음과 같이 정의한다.

A(s,a)=Q(s,a)−V(s)↔V(s)+A(s,a)=Q(s,a)A(s,a)=Q(s,a)-V(s)\leftrightarrow V(s)+A(s,a)=Q(s,a)

이는 특정 상태에서 각 행동을 취하는 상대적인 이점을 의미한다. 이 아키텍쳐는 상태 가치 함수 V(s)와 이점 함수 A(s,a)를 각각 추정하여 이 둘의 결합으로 Q(s,a)를 계산한다. 이점 함수의 도입은 유사한 가치의 행동이 여러 개 있을 때 더 나은 정책 평가를 가능하게 한다.

위 Q(s,a) 식을 이점 함수와 상태 가치 함수에 대한 FC층의 파라미터 α,β\alpha, \beta에 대해 표현하면 다음과 같다.

Q(s,a;θ,α,β)=V(s;θ,β)+A(s,a;θ,α)Q(s,a;\theta,\alpha,\beta)=V(s;\theta,\beta)+A(s,a;\theta,\alpha)

Q(s,a)는 여러 가능한 V와 A의 조합으로 표현될 수 있지만, 그 중 일부만 합리적이기 때문에 A 함수는 제한되어야 한다. 마지막으로 다음과 같은 방법을 사용해 Q(s,a)를 계산하면 다음과 같다.

Q(s,a;θ,α,β)=V(s;θ,β)+A(s,a;θ,α)−1∣A∣∑a′A(s,a′;θ,α)Q(s,a;\theta,\alpha,\beta)=V(s;\theta,\beta)+A(s,a;\theta,\alpha)-{1\over|A|}\sum_{a'}A(s,a';\theta,\alpha)

(1∣A∣∑a′A(s,a′;θ,α){1\over|A|}\sum_{a'}A(s,a';\theta,\alpha): 이점 함수 A의 평균값)

Noisy Network

탐험 능력 향상을 위한 방법 중 하나인 노이즈 네트워크의 아이디어는 신경망에 노이즈를 추가하여 최종 값 출력에 영향을 미쳐 정책의 탐험 능력을 향상시키는 것이다. 노이즈의 크기가 클수록 정책과 원래 정책 간 차이가 커지며, 탐험 능력이 강해진다.

DQN을 예로 들면, 타겟 네트워크와 주 네트워크에 각각 파라미터 δ\delta와 δ−\delta^-를 가진 무작위 노이즈를 추가하는 것으로 새로운 목적 함수 L은 다음과 같다.

L(θ)=Esj,aj,rj,sj+1∼D×[Rj+1+γQ(sj+1,arg⁡max⁡aQ(sj+1,a,ϵ;θ,δ),ϵ−;θ−,δ−−Q(sj,aj,ϵ;θ,δ)]2L(\theta)=E_{s_j,a_j,r_j,s_{j+1}\sim D}\times[R_{j+1}+\gamma Q(s_{j+1},\arg\max_aQ(s_{j+1},a,\epsilon;\theta,\delta),\epsilon^-;\theta^-,\delta^--Q(s_j,a_j,\epsilon;\theta,\delta)]^2

Multistep Learning

Q-Learning에서 이전 정책이 좋지 않고 파라미터의 편차가 클 경우, 목표 값의 편차도 크게 되어서 학습 속도가 느려지는 문제가 발생한다. 이것을 해결하기 위해, 상태-행동 가치 함수를 다음과 같이 확장할 수 있다.

Q(st,at)=Rt+1+γRt+2+⋯+γn−1Rt+n+max⁡aγnQ(st+n+1,a)Q(s_t,a_t)=R_{t+1}+\gamma R_{t+2}+\cdots+\gamma^{n-1}R_{t+n}+\max_a\gamma^nQ(s_{t+n+1},a)

이제 다음 시간 단계의 보상 뿐 아니라 더 많은 이후 시간 단계의 보상도 목표 값에 추가되어 학습 초기 단계에서 목표 값을 더 정확하게 추정할 수 있어서 학습 속도를 가속화할 수 있다.

Distributional Approach

전통적인 강화 학습과는 다르게 가치의 분포가 가치의 기대값보다 더 신뢰할 수 있다는 가정 하에, 분포 강화 학습(Distributed RL)의 아이디어는 가치를 랜덤 변수로 간주하고, 가치의 분포를 추정하는 것을 목표로 한다. 분포 유형을 결정하는 것은 Z의 구체적인 형태를 파악하는 중요한 단계이다. 파라미터 분포는 학습 가능한 파라미터 집합이 분포를 제어한다는 것을 나타내며, Z를 모델링하는데 사용되고 다음과 같이 정의된다.

Zθ(st,at)=zi  with probability  pi(st,at)=eθi(st,at)∑jeθj(st,at)Z_\theta(s_t,a_t)=z_i\ \ \mathrm{with\ probability\ \ }p_i(s_t,a_t)={e^{\theta_i(s_t,a_t)}\over\sum_je^{\theta_j(s_t,a_t)}}

위의 이산 분포를 사용하여 목표 값 분포와 추정 값 분포가 동일하도록 보장하는 범주형 알고리즘이 제안되었다.

Wasserstein distance는 두 확률 분포 간의 거리를 측정하는 더 좋은 방법이다. 그러나 이를 손실 함수로 사용할 때는 계산이 복잡하고 비선형적이며 미분이 어려운 문제가 있다. 그래서 확률적 경사 하강법(SGD) 기술을 최적화에 사용할 수 없었고, Kullback-Leibler(KL) divergence를 거리 측정의 척도로 사용했다. 또 다른 문제 해결 방법은 quantile regression을 사용하여 Wasserstein loss를 최소화하는 것이다.

Other Improvements and Variants

DQN의 성능을 개선하고 적용 범위를 확장하기 위한 여러 수정들이 있었다.

  • Deep Recurrent Q-Network(DQN+LSTM): 부분적으로 관찰 가능한 마르코프 결정 프로세스 문제 해결
  • Bootstrap DQN: 에이전트의 탐색 능력 강화를 위해 제안되었고, Atari 게임에서 학습 시간이 크게 줄고 성능이 개선되었다.
  • DMQ(Difference Maximization Q-Learning) + 선형 함수 근사: 상태 공간을 효과적으로 탐색 가능, 최적에 가까운 정책을 학습할 수 있게되었음

표현적 드리프트와 반복적인 상태 정체를 초래하는 매개변수 지연의 효과를 연구했으며 경험적으로 개선된 교육 정책도 도출되었다.
이러한 각 알고리즘은 다양한 직업에서 성능의 특정 측면을 개선할 수 있지만 이러한 확장 또는 변형 중 어느 것이 보완적이고 효과적으로 결합될 수 있는지는 불분명하다.

이후, Double DQN, Prioritized Experience Replay, Dueling Network, Noisy network, multistep learning, distributional DQN을 연구하고 57개의 Atari 게임에 대한 실험을 통해 앞선 여섯 가지 요소가 보완적임을 증명하고 rainbow라는 결합 알고리즘을 제안했다. 이 결합 기술은 이전에 실험을 통해 Dueling Architecture를 우선 순위가 지정된 experience replay에서 Double DQN과 결합하여 성능을 개선할 수 있음이 증명되었다. 각 구성 요소가 어느 정도 성능을 개선하기 때문에 Rainbow는 제안 시 최적의 성능을 달성했다.

POLICY-BASED DRL METHODS

앞선 Policy Gradient 방법과 Actor-Critic 방법을 확장한 것으로, 고차원 상태 공간과 연속 행동 공간에서 더욱 효과적이다.

Advantage Actor-Critic Method

전통적인 Policy Gradient 알고리즘은 보통 On-Policy 방식으로 업데이트하여 정책 수렴이 느리고 데이터 효율성이 낮다. 이런 문제점을 개선하기 위해 A3C(Asynchronous Advantage Actor-Critic) 방식이 제안되었다.

A3C

A3C는 N개의 스레드에서 환경과 동시에 상호작용하며 데이터를 비동기적으로 수집하여 샘플 수집 속도를 높인다. 수집된 샘플은 각 스레드에서 독립적으로 학습을 완료하고, 전역 모델 파라미터를 비동기적으로 업데이트한다. A3C는 이점 함수를 사용해 편향과 분산의 균형을 맞추고, N-step return 기법을 통해 가치 모델을 효율적으로 업데이트한다. 모델의 탐색 능력을 향상시키기 위해 정책의 엔트로피가 목표 함수에 추가된다.

A3C Architecture

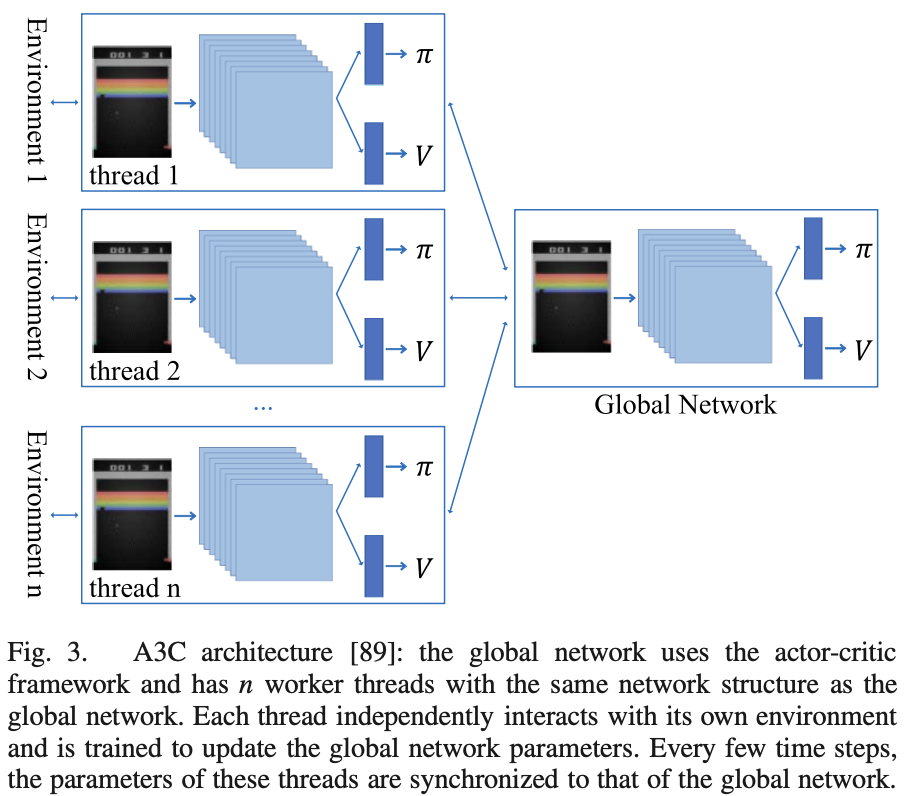
A2C와 ACER

A2C: A3C의 동기식 버전, A3C와 동일하거나 더 나은 성능을 보여주며 GPU 사용을 더 효율적으로 만드는 방식

ACER: Experience Replay를 사용하는 Off-Policy Actor-Critic 알고리즘으로 연속 및 이산 행동 공간 모두에 적용할 수 있으며, A3C의 Off-Policy 버전으로 볼 수 있다.

ACER의 세 가지 해결 방법

  • Q value 추정법(Retrace): 데이터 수집에서 발생할 수 있는 정책 불안정성 문제를 해결한다. 이 방법은 낮은 분산, 데이터 효율성, 안전한 데이터 사용을 특징으로 한다.
  • 중요도 샘플링(Importance Sampling): 정책 그래디언트를 조정해 중요한 샘플의 가중치를 계산한다. 이에 대한 정책 그래디언트는 다음과 같다. 여기서 ρ_t는 중요도 가중치를 나타낸다.
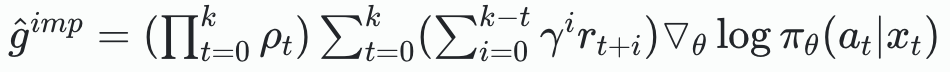
  • 정책 공간에서의 큰 업데이트를 방지: TRPO(Trust Region Policy Optimization) 아이디어를 채택하여, KL divergence 범위를 제한하여 정책 업데이트가 지나치게 커지지 않도록 한다.

Trust Region-Based Algorithms

정책 최적화 방정식에서 α는 업데이트의 step size를 조절한다. 적절한 size는 정책이 더 빠릴 수렴하도록 만들 수 있지만, 부적절한 크기는 정책이 불안정해지거나 심지어 악화될 수 있다. 경험적으로, 적절한 step size는 정책을 단조 증가하도록 만들어야 한다. 이후 TPRO 알고리즘이 제안되고, 한 정책이 다른 정책보다 기대되는 이점이 다음과 같다는 것을 증명했다.

η(π~)−η(π)=Es0,a0,s1,a1,…[∑t=0∞γtAπ(st,at)]\eta(\tilde{\pi})-\eta(\pi)=\mathbb{E}_{s_0,a_0,s_1,a_1,\dots}[\sum_{t=0}^\infty\gamma^tA_\pi(s_t,a_t)]

여기서 η는 정책의 추정 값이며, π π^~는 새로운 정책, ππ는 구 정책, ata_t는 π(at ∣st)π(a_t^~|s_t)로부터 샘플링되며, s0s_0는 초기 상태이다.

정책의 기대 이점 방정식이 양수로 유지된다면, 정책은 단조롭게 증가할 수 있다. TRPO는 KL divergence를 사용해 구 정책과 새로운 정책이 너무 많이 벗어나지 않도록 하는 신뢰 구간 제약을 도입하여, 업데이트 후 정책이 너무 변하지 않도록 하여 학습의 안정성을 향상시키고 단조로운 증가를 보장한다.

PPO(Proximal Policy Optimization)

PPO는 TPRO를 간소화 한 것으로, 잘린 목적 함수를 사용하여, 정책 업데이트 시 불안정한 결과를 피하고 더 효율적으로 학습을 진행한다. PPO의 목적 함수는 다음과 같다.

Lt=1N∑t=1N[min⁡(r(θ)Aπold(st,at),clip(r(θ),1−ϵ,1+ϵ)Aπold(st,at)]L_t={1\over N}\sum_{t=1}^N[\min(r(\theta)A_{\pi_{\mathrm{old}}}(s_t,a_t), \mathrm{clip}(r(\theta),1-\epsilon,1+\epsilon)A_{\pi_{\mathrm{old}}}(s_t,a_t)]

r은 새로운 정책과 구 정책의 비율을 나타내고, A는 이점 함수이다.

불안정한 정책 업데이트 방지를 피하기 위한 2가지 방법

rt(θ)r_t(θ) 비율에 대한 제한을 추가해 [1 - ε, 1 + ε] 범위로 정책 비율을 조정
min 함수를 사용해 두 결과 값 중 작은 값을 선택한다.

Dual-clipped PPO

대규모 Off-Policy 환경에선 πθ(at∣st)>>πθold(at∣st)π_θ(a_t|s_t) >> π_{θ_old}(a_t|s_t)이고 At<0,rt(πθ(at∣st)A_t<0, r_t(π_θ(a_t|s_t)과 πθold(at∣st))π_{θ_old}(a_t|s_t))가 범위를 이탈하는 경우 표준 PPO가 On-Policy 훈련 방식에서 실패할 수 있다.

이 문제를 해결하기 위해 Dual-Clipped PPO가 제안되었으며, 이 방법은 rt(θ)r_t(θ)에 하한을 추가해 정책 업데이트를 안정적으로 만들고 새로운 목적 함수는 다음과 같다.

E^t[max⁡(min⁡(rt(θ)At,clip(rt(θ),1−ϵ,1+ϵ)At),cAt)]\hat{E}_t[\max(\min(r_t(\theta)A_t,\mathrm{clip}(r_t(\theta),1-\epsilon,1+\epsilon)A_t), cA_t)]

여기서 c>1은 상수

ACKTR(Actor-Critic using Kronecker-Factored Trust Region)

ACKTR은 K-FAC(Kronecker-factored Approximate Curvature)를 사용해 정책의 업데이트 크기를 제한하는 신뢰 구간 제약을 채택한다. K-FAC은 Fisher 정보 행렬을 근사할 수 있으며, TRPO와 PPO에서 사용되는 자연 기울기 방법을 사용해 모델을 업데이트한다. 이로 인해 ACKTR은 TRPO와 PPO보다 빠른 훈련 속도를 보인다.

Trust-PCL: 할인된 상대 엔트로피 신뢰 구간을 도입해서 최적화 안정성을 보장하고 Off-Policy 방식을 사용해 샘플 효율성을 개선한다.

Deterministic Policy Gradient(DPG)

결정론적 정책에서는 에이전트가 동일한 상태에서는 항상 동일한 행동을 선택한다.(표현: a=μ(s))

결정론적 정책 그래디언트(DPG) 정리는 다음과 같다.

▽θJ(θ)=E[▽aQμ(s,a)▽θμ(s)∣a=μθ(s)]\triangledown_\theta J(\theta)=\mathbb{E}[\triangledown_aQ_\mu(s,a)\triangledown_\theta\mu(s)|{a=\mu\theta(s)}]

→ μ(s): 결정론적 정책 함수.

이 정리는 일반적인 정책 그래디언트 프레임워크에 통합될 수 있으며, 이를 바탕으로 On-Policy 및 Off-Policy Deterministic Policy Gradient 알고리즘이 제안되었다.

DDPG

DDPG는 결정론적 정책을 학습하며, 이를 Actor-Critic Architecture를 통해 연속적 행동 공간으로 확장한다.

DDPG는 DQN에서 도입된 두 가지 기술을 활용한다.

Experience Replay

→ Replay 버퍼를 사용해 샘플을 수집하고, 이 중 일부를 무작위로 선택해 가치 함수를 최적화하여 데이터 활용도를 개선한다.
→ 결정론적 정책 문제에선 가치 함수가 상태에만 의존하여 Off-Policy 방법을 사용할 수 있다.

Target Network

→ DQN처럼, Q 값의 과대평가를 방지하기 위해 타깃 네트워크를 사용한다.
→ DDPG의 가치 함수가 DQN보다 더 복잡하여, 소프트 업데이트 방식을 통해 매 훈련 반복에서 타깃 네트워크가 메인 네트워크 방향으로 천천히 접근하도록 하여 안정성을 높인다.

소프트 업데이트 방정식

w′←τw+(1−τ)w′θ′←τθ+(1−τ)θ′w'\leftarrow\tau w+(1-\tau)w'\\\theta'\leftarrow\tau\theta+(1-\tau)\theta'

θ, θ’: 메인 액터 네트워크와 타깃 액터 네트워크의 매개변수.
w, w’: 메인 크리틱 네트워크와 타깃 크리틱 네트워크의 매개변수.
τ≪1: 업데이트 계수.
탐색 능력을 향상시키기 위해 DDPG는 Ornstein-Uhlenbeck 노이즈를 추가한다.

TD3(Twin Delayed Deep Deterministic Policy Gradient)

TD3는 DDPG의 과대평가 문제를 해결하기 위해 아래 기술들을 적용한 알고리즘이다.

Clipped Double Q-Learning

→ 2개의 별도의 Critic Network를 사용하여, 더 작은 추정값을 선택해 타깃 값을 업데이트한다.
Delayed Update of Target and Policy Networks
→ Critic Network를 여러번 업데이트 후 정책 네트워크를 업데이트하여 오류 누적을 줄인다.

Target Policy Smoothing

→ 타깃 영역 주변의 작은 영역에 대해 값을 스무딩하고 정규화하여, 가치 함수 추정에 의해 도입된 과적합을 줄인다.

Maximum Entropy DRL

Maximum Entropy RL Framework

전통적인 강화학습의 목적은 기대 보상의 합을 최대화하는 것인데, 최대 엔트로피 강화학습은 보상에 엔트로피 항을 추가하여, 최적의 정책이 각 상태에서 보상과 엔트로피를 동시에 최대화하도록 하고 목적 함수는 다음과 같이 표현된다.

J(π)=∑t=0TE(st,at)∼ρπ[r(st,at)+αH(π(.∣st))](29)J(\pi)=\sum_{t=0}^T\mathbb{E}{(s_t,a_t)\sim\rho\pi}[r(s_t,a_t)+\alpha H(\pi(.|s_t))]\quad(29)

→ H(π(.|s_t))는 엔트로피

→ α는 최적화 목표가 보상 또는 엔트로피에 더 많은 비중을 두도록 조정하는 온도 매개변수이다.

최대 엔트로피 강화학습의 이점

  • 엔트로피 항 덕분에 에이전트가 최적의 확률적 정책을 학습할 수 있다.
  • 엔트로피 항은 정책이 더욱 광범위하게 탐색하도록 장려하며, 희망이 없는 접근법을 버리게 만들어 더 강력한 탐색 능력을 제공하게 한다.
  • 정책이 다중 모드 보상 환경에서 최적의 모드를 찾도록 한다.

강화학습과 엔트로피를 결합하는 여러 아이디어들

  • Boltzmann 탐색 및 Policy Gradient와 Q-Learning(PGQ)
    → 각 시간 단계에서 엔트로피를 최대화하도록 학습한다.
  • 최대 엔트로피와 역강화학습을 결합
    → 전문가 궤적의 확률 분포를 계산했다.

엔트로피 정규화 관점에서 가치기반과 정책 기반 강화학습의 연결성을 연구했으며, 경로 일관성(경로를 따라 계산된 가치가 서로 일관성을 유지하도록 학습하는 것) 학습을 제안했다.

Soft Q-Learning and SAC

전통적인 강화학습에서 주어진 정책은 최적 Q 값에 중심을 둔 분포이다. 이 정책에서 비최적 Q값은 무시하게 되어 에이전트가 여러 모드로 작업을 수행하는 것을 배우지 못하게 만든다. 이 문제를 Q값을 지수화하여 정책을 정의하는 에너지 기반 모델을 제안했다.

π(a∣s)∝exp Q(s,a)(30)\pi(a|s)\propto \mathrm{exp}\ Q(s,a)\quad(30)

이 방식에서 정책은 각 행동에 특정 확률을 할당할 수 있으며, 확률적 정책이 된다. 좋은 정책을 찾는 핵심은 좋은 Q 함수를 찾는 것이다.

  • Soft Q 함수
    Qsoft∗=rt+E(st+1,… )∼ρπ[∑l=1∞γl(rt+l+αH(πMaxent(⋅∣st+1)](31)Q_{\mathrm{soft}}^*=r_t+\mathbb{E}{(s{t+1},\dots)\sim\rho_\pi}[\sum_{l=1}^\infin\gamma^l(r_{t+l}+\alpha H(\pi_{\mathrm{Maxent}}^(\cdot|s_{t+1})]\quad(31)
  • Soft V 함수
    Vsoft∗=α⋅log⁡∫Aexp⁡(1αQsoft(st,a)) da(32)V_{\mathrm{soft}}^*=\alpha\cdot\log\int_A\exp({1\over\alpha}Q_{\mathrm{soft}}^(s_t,a))\ da\quad(32)

이 두 함수의 정의는 Bellman 방정식의 형식을 만족함이 증명되었으며, 이는 Soft Bellman backup이라고 불린다.

최적 정책의 형태

πMaxEnt∗(at∣st)=exp⁡(1αQsoft∗(st,at)−Vsoft∗(st))π_{\mathrm{MaxEnt}}^∗(a_t∣s_t)=\exp({1\overα}Q_{\mathrm{soft}}^∗(s_t,a_t)−V_{\mathrm{soft}}^∗(s_t))

Soft Q 함수 근사 및 SAC 제안

Soft Q 함수는 θ로 매개변수화된 신경망으로 모델링이 된다. Soft Q 반복 과정을 확률적 최적화 문제로 변환하기 위해 중요도 샘플링을 사용하며, 확률적 경사 하강법을 통해 Q 네트워크를 업데이트한다. 상태 조건 확률적 신경망은 에너지 기반 정책을 근사하여 편향되지 않은 행동 샘플을 생성한다.

Soft Q-Learning의 손실 기울기가 정책 경사 항목과 기준선 오류 기울기 항목으로 표현되어 soft Q-Learning과 정책 경사 방법이 등가임이 증명되었다.

다중 에이전트 강화학습에서 soft Q-Learning을 채택하여 협력적 작업에서 최첨단 방법인 Multi-Agent Deep Deterministic Policy Gradient(MADDPG)보다 더 나은 성능을 달성했다.

Soft 정책 반복이 테이블 형식에서 최적 정책으로 수렴함을 증명이 되었다.

대규모 연속 도메인에 적용하기 위해 θ와 ϕ로 매개변수화된 신경망을 사용하여 Soft Q 함수 Qθ(st,at)Q_θ(s_t,a_t)와 정책 πϕ(at∣st)π_ϕ(a_t|s_t)를 표현했다.

또한 Off-Policy, Actor-Critic, 최대 엔트로피 방법을 결합한 최초의 RL 알고리즘인 Soft Actor-Critic(SAC)를 제안했다.

Further Research Topics

앞선 DRL 방법은 풍부한 보상 신호를 얻고 무제한 롤아웃을 수행할 수 있는 게임 및 시뮬레이션 환경에만 적합하다. 그러나 더 복잡한 환경이나 실제 환경에선 제한된 샘플, 희소한 보상, 다중 에이전트와 같은 문제가 종종 발생한다.

이런 문제를 해결하기 위해 Model-Based RL, Hierarchical RL, Meta RL과 같은 새로운 연구 방향을 개척했다.

Model-Based Methods

위에 소개된 모든 알고리즘은 Model-free 방식이어서, 대량의 학습 샘플이 필요하기 때문에 실제 문제에 적용하는 데 어려움이 있다. 또한 Off-Policy Model-free 방법에서는 경험 재생 중 전이에서 발생하는 오류를 제거하기 어려운 부담이 된다.

Model-Based 방법은 환경이 어떻게 변화하는지 설명할 수 있는 동적 모델을 학습하는 것을 목적으로 한다. 학습된 모델이 환경을 잘 근사화할 경우, 일부 계획 방법을 통해 최적 정책을 직접 찾을 수 있다. 더불어, 학습된 모델은 On-Policy 학습에도 직접 사용할 수 있다.

Model-free 알고리즘의 높은 샘플 복잡도는 특히 고차원 함수 근사기를 다룰 때 사용 범위를 제한한다.

연속 제어 작업에서 샘플 복잡도를 연구가 진행된 이후, 두 가지 상호 보완적인 기술을 포함하는 알고리즘을 제안되었다.

  1. 액터-크리틱 구조를 단순화하여 정규화된 이점 함수(NAFs)를 제안했으며, 이를 통해 Q-Learning이 연속 행동 공간에 적응할 수 있게 했다.
  2. 연속 Q-Learning을 Off-Policy 경험에서 학습된 모델과 결합하여 연속 행동 공간에서 알고리즘의 학습 과정을 가속화했다.

모델 기반 정책 최적화(MBPO): 복합적 오류를 해결하기 위해 짧은 롤아웃을 통해 모델 예측의 신뢰도를 유지하는 알고리즘

Dreamer: 경험으로부터 세계 모델을 학습한 뒤, 학습된 세계 모델과 상호작용하여 최적의 정책을 학습하기 위해 액터-크리틱 알고리즘을 사용하는 알고리즘으로, 학습 과정이 학습된 모델 내에서 이루어지며, 이를 통해 다단계 누적 보상을 얻고 장기 계획을 수행할 수 있다.

Hierarchical DRL

HRL은 희소한 보상을 가지며 목표 지향적 탐색을 요구하는 작업을 해결하기 위해 제안되었다. 하지만 HRL은 표현 능력의 부족으로 인해 하위 목표의 선택은 전문가 지식에 의존해야 했다.

딥러닝의 도움으로 HRL은 큰 상태 공간과 행동 공간 문제를 해결할 수 있으며, 고차원 입력을 직접 처리할 수 있게 되었다. 또한 딥러닝의 표현 능력은 하위 목표의 형태에 더 많은 선택지를 적용한다. 이로 인해 계층적 심층 강화학습은 심층 강화학습의 중요한 연구 방향이 되었다.

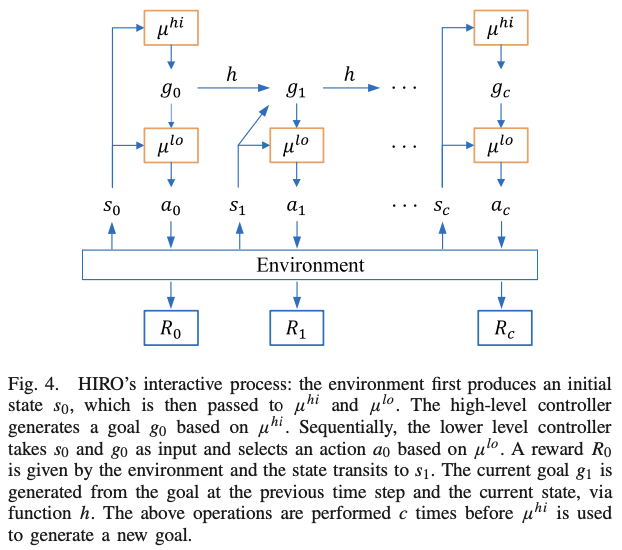
HDRL 모델

  • HIRO 모델: 계층을 하위 제어기와과 상위 제어기를 사용하는 HDRL 모델
  • 옵션-크리틱 아키텍처: 옵션 정책 가중치 정리를 도출하고, 옵션의 내부 정책과 종료 조건을 학습할 수 있는 구조
  • 경험 재생에서 전이 튜플에 목표를 추가해 서로 다른 목표를 가진 전이 튜플을 사용해 다른 목표를 학습할 수 있게 만든다.
  • Diversity Is All You Need(DIAYN) 알고리즘: 에이전트가 실제 보상을 얻을 방법이 없더라도 다양한 작업 해결 기술을 학습할 수 있도록 하는 알고리즘.

MultiAgent DRL

다중 에이전트 심층 강화학습(MADRL)은 DRL의 아이디어를 다중 에이전트 시스템의 학습 및 제어에 적용하여, 기존 방법이 직면했던 고차원 입력, 연속 행동 공간 등의 어려움을 극복한다.

극복하기 위해 DDPG의 다중 에이전트 버전인 MADDPG를 제안했으며, 이를 통해 각 에이전트는 크리틱 섹션에서 다른 모든 에이전트의 행동 정보를 얻을 수 있어 중앙 집중식 학습과 분산 실행을 달성할 수 있다.

  • 중앙 집중식 학습: 각 에이전트는 자신과 다른 에이전트의 상호작용을 고려하며 더 효과적으로 학습한다.
  • 분산 실행: 학습이 끝난 후, 각 에이전트는 자신의 정책만을 사용해 독립적으로 행동한다.

그러나 MADRL이 점점 더 복잡한 상태 공간 및 행동 공간 작업에 사용되면서 많은 문제가 나타났다. 전체 다중 에이전트 작업에 더 큰 기여를 하는 에이전트를 장려하기 위해, 반사실적 기준선 아이디어를 제안하여 신용 할당 문제를 해결했다.

신용 할당 문제: 각 에이전트의 행동의 기여도를 평가하기 어려운 문제

Value Decomposition Networks(VDNs)는 각 에이전트의 가치 함수를 통합하여 공동 Q 함수(joint Q function)를 생성함으로써, 환경의 부분 관찰성으로 인해 발생하는 가짜 보상 문제와 게으른 에이전트 문제를 해결했다.

  • 가짜 보상 문제: 환경의 부분 관찰성 때문에, 개별 에이전트의 행동이 전체 보상에 미친 영향을 정확히 평가하기 어려운 문제
  • 게으른 에이전트 문제: 일부 에이전트가 아무것도 하지 않거나 비협조적인 행동을 취해도, 다른 에이전트의 노력으로 인해 전체 보상이 유지되는 문제다.

QMIX는 VDN의 확장판으로, 혼합 네트워크를 사용해 개별 에이전트의 로컬 가치 함수를 결합하고, 학습 과정에서 전역 상태 정보를 추가해 알고리즘 성능을 향상시켰다.

Learning from demonstrations

희소한 보상이나 다목적 작업에서는 누적 보상을 기반으로 한 학습 알고리즘이 대규모 탐색 공간과 보상 설정의 어려움으로 인해 에이전트가 지능적으로 행동하도록 만드는 데 종종 실패한다. 에이전트가 더 빠르게 최적 또는 준최적 정책을 학습하도록 보장하기 위해, 전문가의 시연에서 보상 함수나 정책을 학습하는 것이 일반적으로 좋은 아이디어다. 이는 각각 역 강화 학습과 모방 학습에서 채택된 방법이다.

역 강화학습

역 강화학습을 기반으로 한 초기 방법에는 주로 Apprenticeship learning, Structured classification, Maximum margin planning, 및 Maximum entropy methods가 포함된다.
최근 몇 년 간 딥러닝 기술을 사용하는 역 강화학습 방법들이 제안되었다. 역 강화학습 방법들 중 하나로 적대적 역 강화학습(AIRL)을 제안되었으며, AIRL이 환경 동적 변화에 강인한 보상 함수를 복구할 수 있음을 입증했다.

모방 학습

모방 학습의 주요 아이디어는 전문가의 시연에서 정책을 학습하기 위해 지도 학습을 사용하는 것이다. 전통적인 모방 학습 방법은 행동 정책과 학습된 정책 간의 복합 오류를 제거하는데 중점을 두며, 데이터 증강 방법도 사용된다. 모방 학습은 지도 학습 방식이기 때문에 딥러닝과 쉽게 결합될 수 있다.

모방학습의 프레임워크로 Generative Adversarial Imitation Learning(GAIL)이라는 프레임워크가 제안되었다. GAIL은 GANs와 모방 학습을 결합하여 데이터를 통해 직접 정책을 추출하는 방법으로, 큰 고차원 환경에서 다른 모방 학습 알고리즘보다 뛰어난 성능을 보였다.

전문가 시연 데이터가 제한적이고 불균형적일 경우 비선형 보상을 학습할 수 있는 AdaBoost Maximum Entropy Deep Inverse Reinforcement Learning(AME-DIRL) 알고리즘도 제안되었다.

Meta-RL

메타 강화학습의 주요 아이디어는 많은 수의 강화학습 작업에서 학습된 사전 지식을 새로운 RL 작업에 적용하고, 에이전트의 학습 속도와 일반화 능력을 향상시키는 것이다. 메타 강화학습은 주로 DRL의 아래와 같은 단점들을 해결하고 최적화하는 데 중점을 둔다.

  • 낮은 샘플 활용도: DRL 알고리즘은 많은 데이터를 요구하는데, 실시간 환경에서 많은 데이터를 얻기 어렵고, 효율적으로 학습하지 못하는 문제
  • 보상 함수 설계의 어려움: 적절한 보상 함수를 설계하는 것은 매우 어려운 문제
  • 알려지지 않은 작업에서의 탐색 전략: 환경에 대한 지식이 부족한 경우엔 탐색이 중요하지만, 이를 잘 수행하는 것이 어렵다.
  • 일반화 능력의 부족: DRL은 주어진 특정 환경에서만 최적화되기 때문에, 새로운 환경이나 미지의 상황에 적응하는데 어려운 문제

Offline RL

오프라인 강화학습은 훈련 과정에서 상호작용 없이 과거에 수집된 오프라인 데이터를 사용하여 에이전트를 훈련하는 방법이다. 오프라인 강화학습의 주요 문제는 오프라인 데이터셋의 행동정책 πβπ_β와 에이전트 정책 π 간의 분포 변화다.

오프라인 강화학습 방법의 세 가지 범주

  1. 중요도 샘플링을 사용해 정책의 수익 J(π)를 직접 평가하거나, 오프라인 데이터에서 샘플링된 행동 정책 π_β를 통해 해당 정책 기울기를 추정하는 방법
  2. 동적 프로그래밍 기반의 강화학습 알고리즘을 사용하는 것(ex. Q-Learning 기반 알고리즘)으로 온라인 데이터가 없으면 직접 적용할 수 없기 때문에 정책 제약 방법과 불확실성 기반 방법이 제안되었다.
    • 정책 제약 방법: 학습된 정책을 행동 정책 근처로 제한하여 분포 변화를 없애는 방법
    • 불확실성 기반 방법: Q-value의 인식 불확실성을 사용하여 분포 변화를 감지하는 방법
  3. 모델 기반 방법
    모델 기반 방법은 하나의 환경에서 상태 전이 확률을 학습하며, 감독 학습 방법을 사용할 수 있기 때문에 오프라인 데이터셋을 더 잘 활용할 수 있다.

Transfer Learning in RL

전이 학습은 소스 작업에서 학습한 경험을 적용하여 대상 작업의 훈련 효율성을 향상시킬 수 있다. 따라서 새로운 작업에서 학습 속도를 개선하기 위해 강화학습을 위한 전이 학습(TL for RL)은 매력적인 연구 방향이 되었다. 전이 학습이 전이하는 지식에 따라, TL은 DRL 알고리즘을 다음과 같은 측면에서도 도울 수 있다.

  • 보상 형성: 기존 작업에서 얻은 지식을 이용해 새로운 작업의 보상 함수를 개선하는 방식
  • 시연 학습: 이전에 학습된 전문가의 행동 데이터를 새로운 작업에 적용하여 학습 시간을 단축시킬 수 있다.
  • 정책 전이: 이미 학습된 정책이 새로운 환경에서도 유효하다면, 그 정책을 가져와 사용하여 학습을 가속화할 수 있다.
  • 작업 간 매핑: 이전에 학습한 작업들의 특징을 매핑하여 새로운 작업에 적합한 방법을 찾는다.
  • 표현 전이: 이전 작업에서 얻는 특징 추출 방식을 새로운 작업에 적용하여, 에이전트가 빠르게 학습할 수 있도록 돕는다.

Conclusion

DRL은 딥러닝과 강화학습의 장점을 결합하여 입력 데이터를 바탕으로 직접 결정을 내릴 수 있다. 이 글에서는 현재 인기 있는 DRL 라이브러리에서 구현된 알고리즘을 소개하며, 가치 기반, 전략 기반, 최대 엔트로피 기반 알고리즘을 포함하고, 최근 몇 년간의 DRL 연구 하위 분야들을 간략하게 나열한다. DRL에 대한 연구는 세상을 더 잘 이해하는 자율 시스템을 구축하는 중요한 단계이다.

profile
Seon
끼룩..
이전 포스트

강화 학습(RL) 알고리즘

0개의 댓글