램지 정리, Ramsey's theorem
완전한 무질서는 없다. Complete disorder is impossible.
램지 정리: k와 n이 2보다 큰 양의 정수일 때, 다음을 만족하는 가장 작은 양의 정수 m이 반드시 존재한다.
- 만일 노드들의 개수가 m이고 서로 다른 모든 두 노드들이 간선으로 연결된 무향 그래프 G의 모든 간선들, 즉, m*(m-1)/2 개의 간선들을 파란색과 빨간색 두가지로 칠한다면,
- 어떻게 색칠하던지 아래 (1),(2) 중 하나의 특징을 가지는 무향 그래프 H=(V',E')이 반드시 존재한다.
(1) |V'|=k, |E'|=k(k-1)/2. E'의 모든 원소들이 파란색으로 칠해지며 V'<=V, E'<=E.
(2) |V'|=n, |E'|=n(n-1)/2. E'의 모든 원소들이 파란색으로 칠해지며 V'<=V, E'<=E.
(V'은 노드들을 의미하고, E'은 간선들을 의미한다.)
ex) m=6, k=3, n=3.
노드들에 0,1,2,3,4,5 라는 명칭을 부여하자.
여기서 5 기준으로 생각했을 때
(1) 세 명 이상과 서로 아는 경우, (2) 두 명 이하와 서로 아는 경우
로 나눌 수 있다.
(a와 b가 서로 안다고 함은 a도 b를 알고 b도 a를 아는 것이다. 만약 a가 b를 아는데 b가 a를 모르면 그것은 서로 모르는 것이다.)
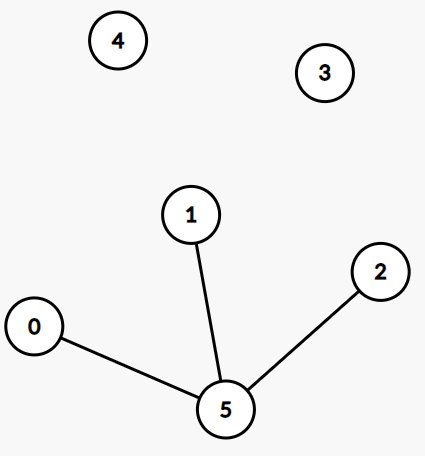
(1)의 경우
여기서 0,1,2 사이 관계를 생각했을 때
(a) 서로 서로 모르거나
(b) 그렇지 않거나 0-1 2 라면
5,0,1은 서로 서로 알게 된다.
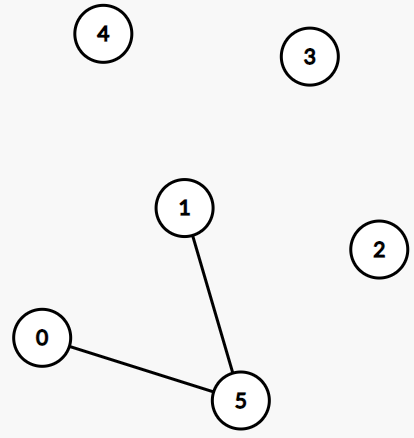
(2)의 경우
여기서 2,3,4 사이 관계를 생각했을 때
(a) 서로 서로 알거나
(b) 서로 서로 모르거나
로 분류할 수 있음을 알 수 있다.
예제에서 서로 안다는 것과 모른다는 것은 램지정리의 개념 설명에서의 빨간색으로 칠하기와 파란색으로 칠하기에 대응된다.
https://csacademy.com/app/graph_editor/
그래프는 cs academy에서 그렸다.
