KNN 알고리즘이란?
-
머신러닝 지도학습 알고리즘 중 하나
-
가장 가까운 속성에 따라 분류하여 레이블링을 하는 알고리즘
-
거리기반 분류 분석 모델
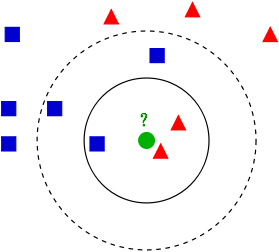
위 이미지는 녹색점이 녹색점 주변의 다른 점들과 유사한 특징을 지니며, 주변 샘플들을 통해 녹색점을 어디에 분류할지 정하는 Task이다.
몇 개의 점을 기준으로 판단할 것인가가 바로 K의 값이 되는 것이다 .
K=3 이라면 녹색점 주변에 가장 가까이 있는 빨간점 2개와 파란점 1개의 특성과 묶인다. (검은 실선)
그로인해 녹색점은 빨간색의 특성을 가지고 있는 것으로 분류가 될 것이다.
하지만, K=5일 경우, 파란점 3개와 빨간점 2개의 특성과 묶인다. (검은 점선)
그로인해, 녹색점은 파란색의 특성을 가지고 있는 것으로 분류가 될 것이다.
이처럼 K의 값에 따라 변화가 생긴다.
만약 K가 너무 크다면, 데이터가 무수히 많아 여러 종류에 데이터가 존재하게 되고 분류를 잘 못할 것이다.
하지만 반대로 K가 너무 작다면 샘플 하나하나에 과한 영향을 받아 이상치의 영향이 크게 되어 과적합이 발생하게 될 것이다.
거리기반 분류 분석 모델
-
KNN 알고리즘은 거리기반 분류 분석 모델로 상대적으로 거리가 더 짧은 이웃이 더 가까운 이우승로 취급이 된다.
-
어떤 새로운 데이터로 부터 거리가 가까운 K개의 다른 데이터 속성(레이블)을 참고해 K개의 데이터 중 가장 빈도 수가 높게 나온 데이터의 속성(레이블)로 분류하는 알고리즘
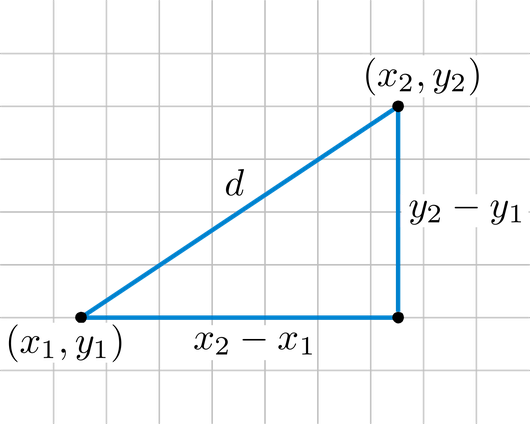
유클리드 거리(Euclidean Distance)
-
L2 Distance
-
연속형 변수일 경우 사용
-
일반적으로 유클리드 거리 계산법을 사용
-
두 점 과 가 있을 때 계산식은 아래와 같다.
맨해튼 거리
-
L1 Distance
-
연속형 변수일 경우 사용
-
사각형의 모양이 촘촘하게 들어선 빌딩과 건물의 모습을 지니고 있는 맨해튼 거리 모습에서 공식이 유래되었다.
-
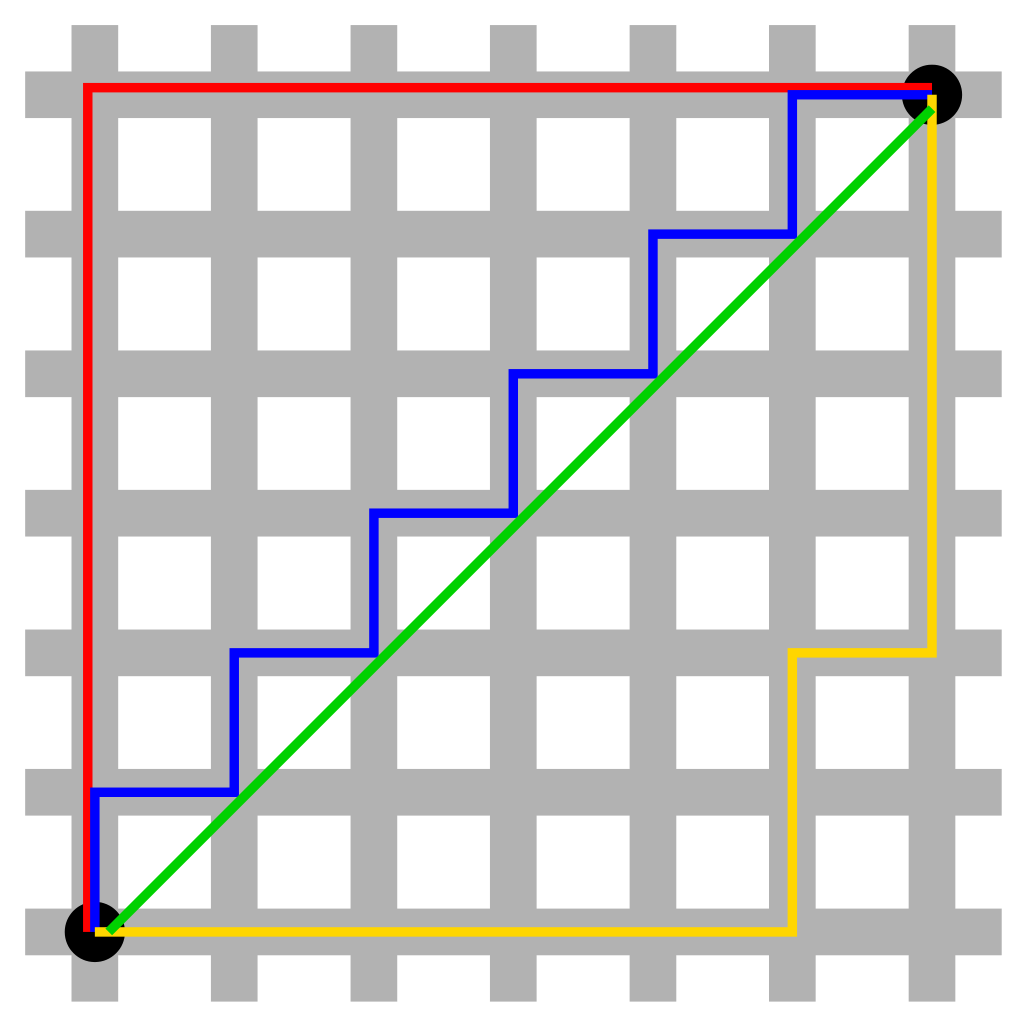
검은색 두 점 사이의 거리를 측정할 경우
- 초록색 = 유클리드 거리 (가장 가까운 직선거리)
- 빨간색, 파란색, 노란색 = 맨해튼 거리 (길이 존재하는 최단 루트)
-
두 점 과 가 있을 때 계산식은 아래와 같다.
해밍 거리
-
한 문자열을 다른 문자열로 바꾸기 위해서 몇글자를 바꾸어야 하는지를 나타낸 것
-
'1011101'과 '1001001'사이의 해밍 거리는 2이다. (1011101, 1001001)
-
'2143896'과 '2233796'사이의 해밍 거리는 3이다. (2143896, 2233796)
-
"toned"와 "roses"사이의 해밍 거리는 3이다. (toned, roses)
