차원축소

• 많은 Feature로 구성된 다차원 데이터세트의 차원을 축소해 새로운 차원의 데이터로 재생성하는 과정

  • 일반적으로 차원이 증가할 수록 데이터 간의 거리가 기하급수적으로 증가하기 때문에 희소한 구조를 가지게 되어 예측 신뢰도가 하락함
  • 더불어 학습데이터의 크기가 줄어들어 학습 처리 시간 감소 가능

• 차원 축소의 방법은 feature 선택과 추출로 나누어 진다.

• feature 선택

  • 특정 feature에 종속성이 강한 불필요한 feature는 제거하는 것

  • 장점 : 선택한 feature의 해석이 용이

  • 단점 : feature간의 상관관계를 고려하기 어려움

• feature 추출

  • 기존 feature를 저차원의 중요 feature로 압축해서 추출하는 것
    새롭게 추출된 feature는 기존의 feature가 압축된 것이므로 기존의 feature와는 완전히 다른 값이 됨
  • 장점 : feature간의 상관관계를 고려하기 용이, feature개수를 더 많이 줄일 수 있음
  • 단점 : 추출된 변수의 해석이 어려움

---

PCA (주성분 분석)

• 여러 변수간에 존재하는 상관관계를 이용해 이를 대표하는 주성분을 추출해 차원을 축소하는 기법

• 데이터를 축에 사영했을 때 가장 높은 분산을 가지는 데이터의 축(주성분)을 찾아 그 축으로 차원을 축소하는 것

• 높은 분산을 가지는 데이터의 축(주성분)을 찾는 이유는 정보의 손실을 최소화 하기 위해

• 사영 했을 때 분산이 크다는 것은 원래 데이터의 분포를 잘 설명할 수 있다는 것을 뜻함

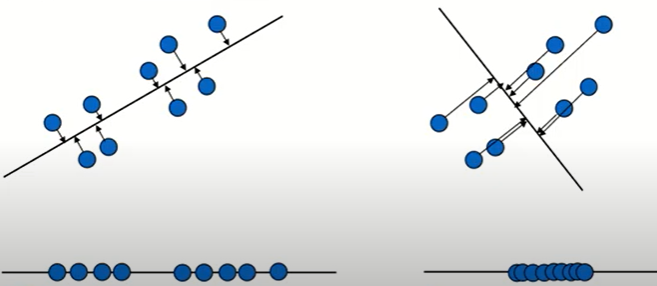
위 그림의 좌측 데이터의 사영한 값을 보면 분산이 크게 나타나고 있어 분포를 잘 설명하기 용이해 보인다.

---

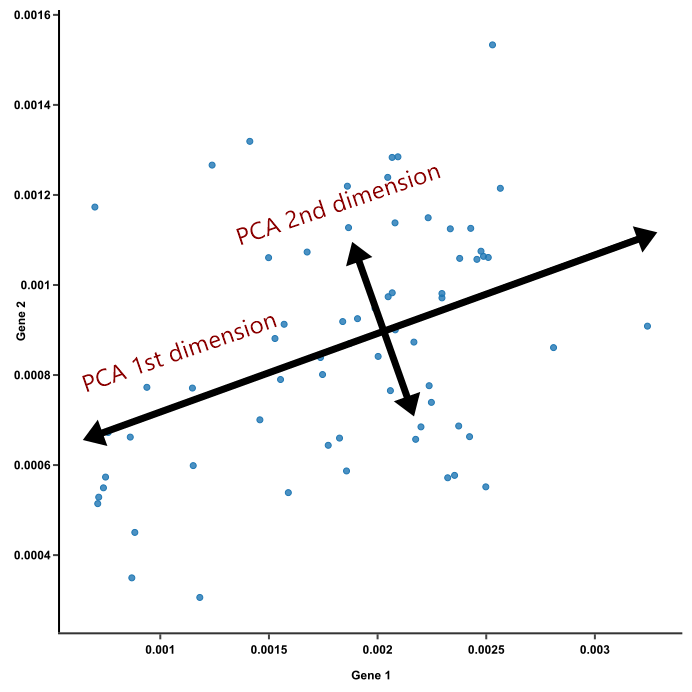
축 생성 과정

1. 먼저 가장 큰 분산을 기반으로 첫 번째 축을 생성

2. 두번째 축은 이 vector축에 직각이 되는 vector를 축으로 설정

3. 다시 두번째 축과 직각이 되는 vector를 축으로 설정

4. 반복을 통해 vector축에 원본 데이터를 투영하면 vector 축의 개수만큼의 차원으로 원본 데이터가 차원 축소

왜 직각이 되는 vector를 다음 축으로 설정하는가?

먼저 첫 번째 축에 데이터를 사영했을 경우 같은 점으로 겹쳐 설명하기 어려운 데이터가 10개 있다고 가정

이후 직교하는 축으로 사용하게 되면 겹쳤던 10개의 데이터는 절대 같은 점으로 사영이 될 수 없어서 10개의 데이터를 설명할 수 있게 된다.

해당 원리로 직교하는 축을 다음 축으로 설정하는 방식을 통해 vector 축을 생성

축을 어떤 원리로 찾는가?

입력 데이터의 공분산 행렬을 고유값 분해했을때 구해진 고유벡터(=PCA의 주성분 vector)로써 입력 데이터가 어떤 방향으로 분산되어 있는지를 나타낸다.

즉, 고유값이 고유벡터의 크기를 나타내고 입력 데이터의 분산을 나타낸다.

공분산 행렬이란?

• 데이터의 구조를 설명해주며, 특히 특징 쌍(feature pairs)들의 변동이 얼마나 닮았는가(다른 말로는 얼마만큼이나 함께 변하는가)를 행렬에 나타낸다.
• 정방행렬 이면서 대칭행렬
• 대칭행렬은 항상 고유벡터를 직교행렬로
• 고유값을 정방 행렬로 대각화할 수 있는 특성을 가지고 있다.

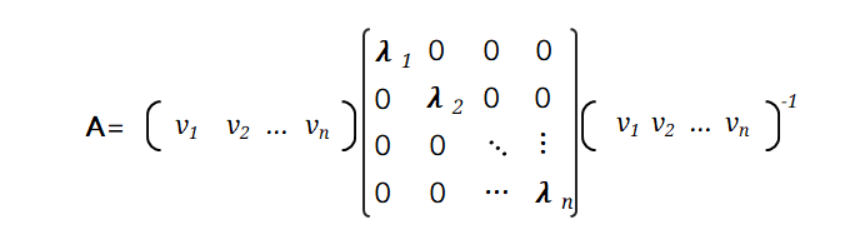
공분산 행렬이 A일 경우 고유값 분해는 위와 같이 할 수 있다.

• $v_1,v_2,\dots,v_n$ = 고유벡터
• $λ_1,λ_2,\dots,λ_n$ = 고유값
• $v_1$이 가장 분산이 큰 방향을 가진 고유 벡터이고, $v_2$는 $v_1$에 수직이면서 다음으로 분산이 큰 방향을 가진 고유벡터

입력 데이터의 공분산 행렬이 고유벡터와 고유값으로 분해될 수 있으며, 이렇게 분해된 고유벡터를 이용해 입력 데이터를 선형 변환하는 방식이 PCA라는 것

---

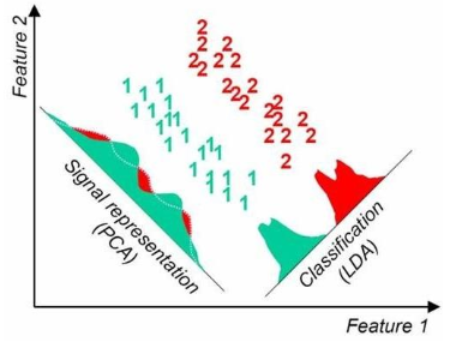
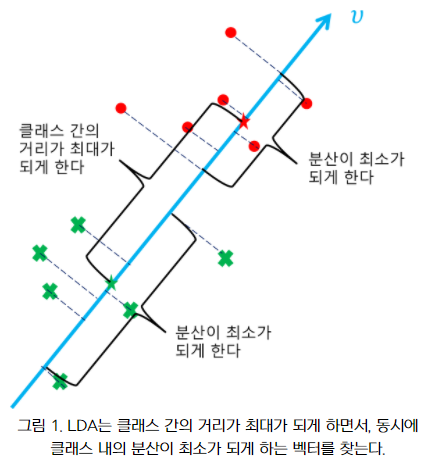
LDA (선형 판별 분석법)

• PCA와 유사하게 입력 데이터를 저차원 공간에 투영해 차원을 축소하는 기법

• LDA는 지도학습 분류에서 사용하기 용이하도록 개별 클래스를 분별할 수 있는 기준을 최대한 유지하면서 차원을 축소

• 즉, 클래스 분리를 최대화하는 축을 찾기 위해 클래스간 분산을 최대화하고 클래스 내부 분산은 최대한 작게 가져가는 방식

• 공분산 행렬이 아닌 클래스 내부와 클래스 간 분산 행렬에 기반해 고유벡터를 구하고 입력 데이터를 투영

분석 과정

1. 클래스 내부와 클래스 간 분산 행렬 계산

2. 클래스 내부 분산 행렬의 역치 행렬과 클래스 간 분산 행렬의 곱을 분해하여 고유벡터와 고유값 계산

3. 고유값이 가장 큰 순으로 K개 추출

4. 추출된 고유벡터를 이용해 입력 데이터를 선형 변환

---

PCA와 LDA의 차이점

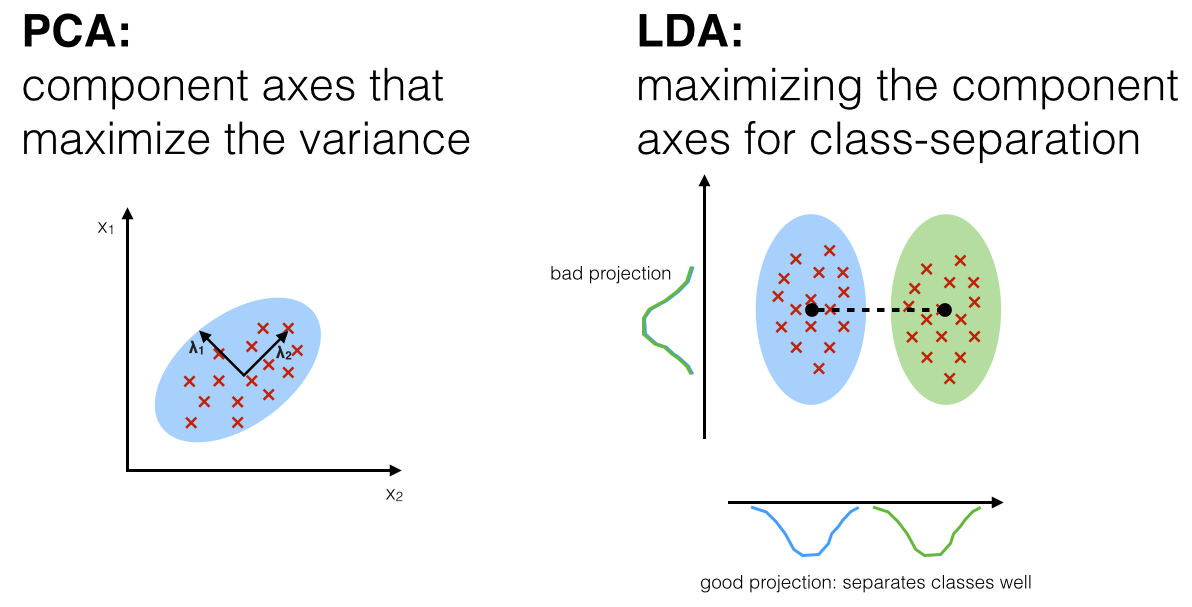
PCA

• 입력 데이터를 저차원 공간에 투영해 차원을 축소하는 기법

• Unsupervised Learning

• 데이터의 클래스 차이가 평균보다 분산의 차이에 있을 때 더 뛰어난 성능을 보임

• 입력 데이터의 변동성(분산)이 가장 큰 축을 찾음
  즉, 데이터가 넓게 분포(분산이 큼)되어 있도록 하는 새로운 축을 찾는 것

LDA

• 지도학습 분류에서 사용하기 쉽도록 개별 클래스르 분별할 수 있는 기준을 최대한 유지하며 차운을 축소하는 기법

• Supervised Learning

• 데이터의 클래스 차이가 분산보다 평균의 차이에 있을 때 더 뛰어난 성능을 보임

• 입력 데이터의 결정 값 클래스를 최대한으로 분리할 수 있는 축을 찾음
  즉, 클래스들을 가장 잘 구분할 수 있는 새로운 축을 찾음