6. 의사결정트리(Decision Tree)
의사결정트리란?
-
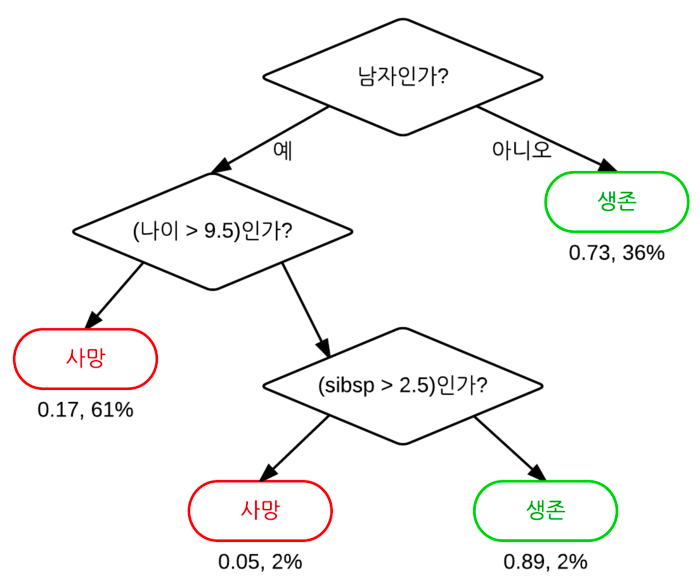
일련의 분류 규칙을 통해 데이터를 분류, 회귀하는 지도 학습 중 하나
-
특정 기준(질문)에 따라 데이터를 구분하는 모델
-
한번의 분기 때마다 변수 영역을 2개로 구분
- Root Node : 가장 처음 분류 기준
- Intermediate Node : 중간 분류 기준
- Leaf Node : 맨 마지막 분류 기준
-
Leaf Node가 가장 섞이지 않은 상태로 완전히 분류해 복합성(Entropy)를 낮도록 만드는 것이 목표
프로세스
-
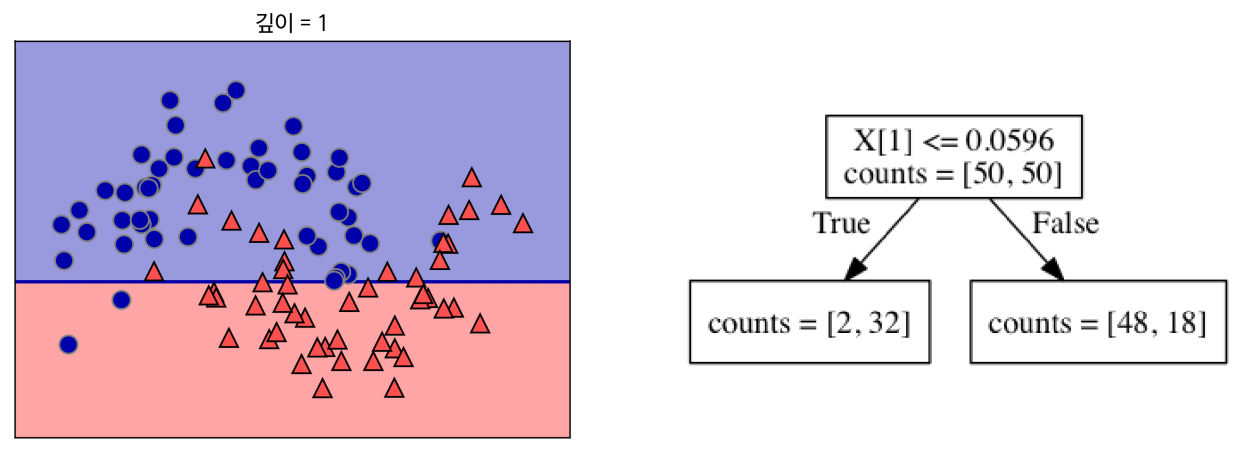
가장 데이터를 잘 구분할 수 있는 기준 설정
-
각 범주에서 다시 데이터를 가장 잘 구분할 수 있는 기준 설정
- 각 테스트는 하나의 특성에 대해서만 이루어지므로 나누어진 영역은 항상 축에 평행
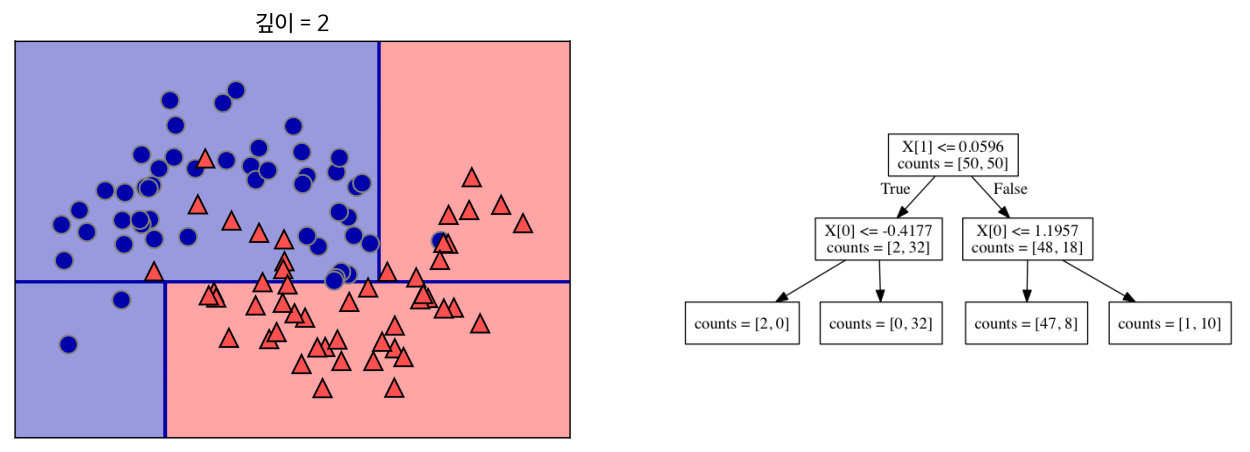
- 각 테스트는 하나의 특성에 대해서만 이루어지므로 나누어진 영역은 항상 축에 평행
-
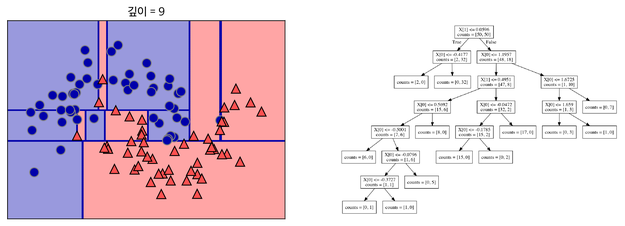
각 분할된 영역(결정 트리의 Leaf)가 하나의 클래스 or 회귀분석 결과를 가질 때 까지 반복
- target 하나로만 이루어진 Leaf Node = Pure Node
- 지나치게 많이 반복할 경우 Overfitting이 됨
불순도(Impurity)
-
결정트리에서 분기 기준을 선택하기 위해 불순도라는 개념을 사용
-
복잡성을 의미
-
해당 범주안에 서로 다른 데이터가 얼마나 섞여 있는지를 의미
-
-
분기 기준을 설정할 시, 현재노드의 불순도에 비해 자식 노드의 불순도가 낮아지게 기준을 설정 해야 함
-
현재 노드의 불순도와 자식 노드의 불순도의 차이 = 정보획득(Information Gain)
불순도 함수 (Gini, Entropy)
지니 지수 (Gini)

-
지니 지수의 최대값은 0.5
-
통계적 분산 정도를 정량화해서 표현한 값으로 0과 1사이의 값을 가짐
-
지니 지수가 작을 수록 잘 분류한 것
엔트로피 지수 (Entropy)
- D : 주어진 데이터들의 집합
- k-class set in sample : D에서 K클래스에 속하는 샘플의 개수
- sample : 주어진 데이터들의 집합의 데이터 개수
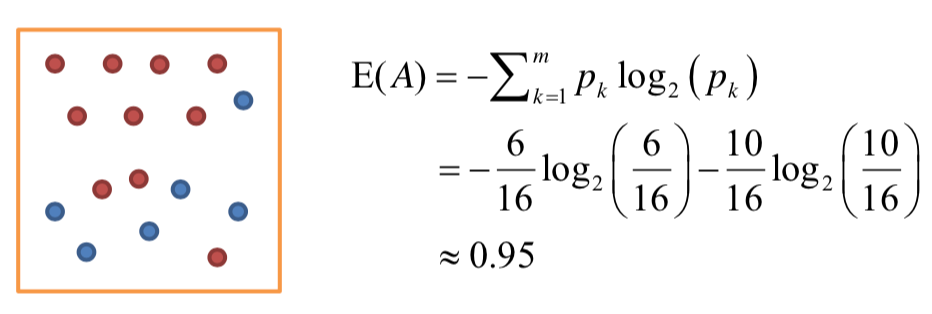
- 엔트로피 값이 작을 수록 잘 분류한 것
정보 획득(Information Gain)
- 현재 노드의 불순도와 자식 노드의 불순도의 차이
- 만약 불순도가 0.8인 상태에서 0.2로 바뀌었다면 정보 획득은 0.6
결정트리 구성 단계 예시
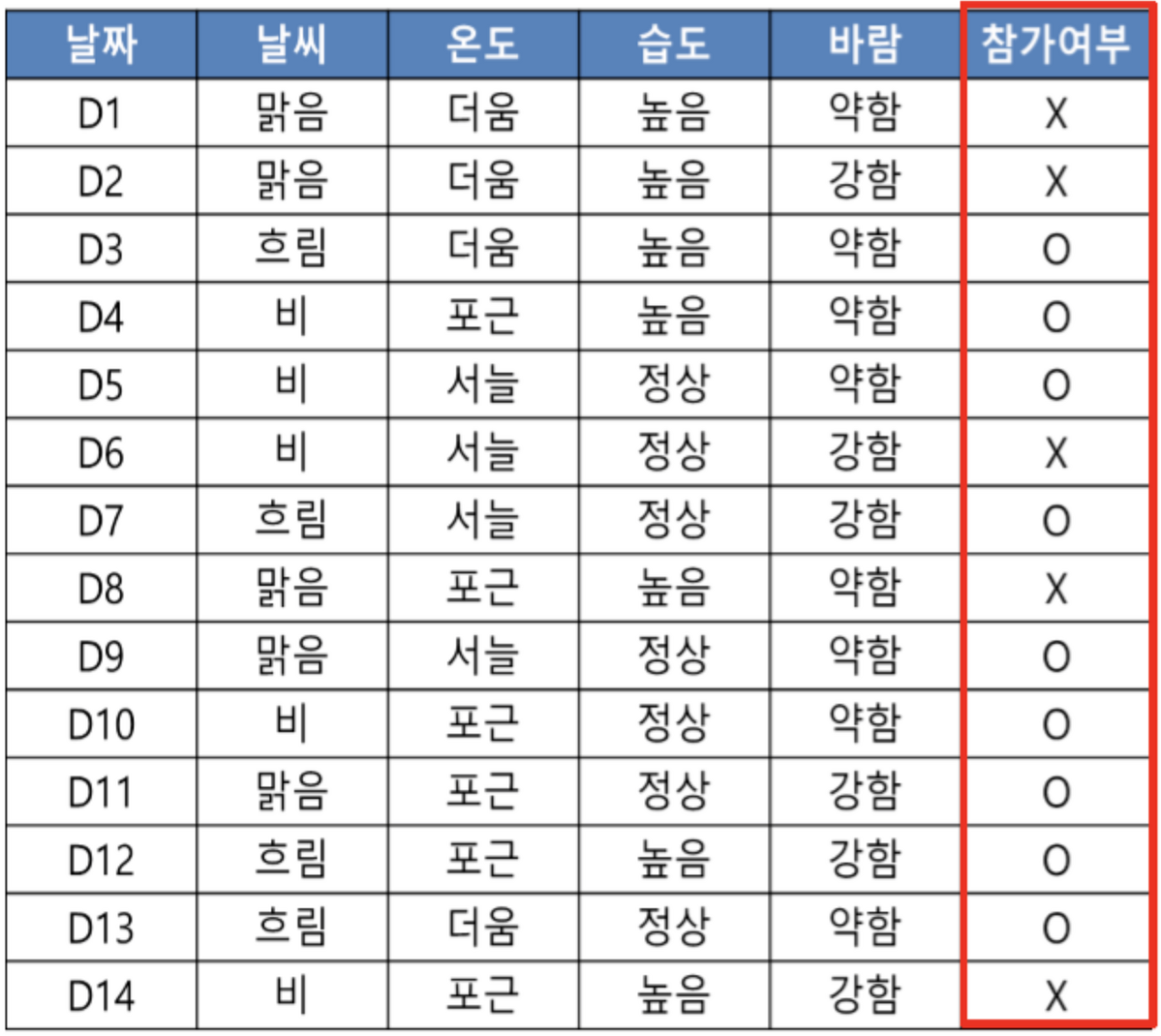
1. Root Node의 불순도 계산
$E(경기) = -\frac{9}{14}log_2(\frac{9}{14}) - \frac{5}{14}log_2(\frac{5}{14}) = 0.940$2. 나머지 속성에 대해 분할 후 자식노드의 불순도 계산
-
날씨

-
온도

-
습도

-
바람
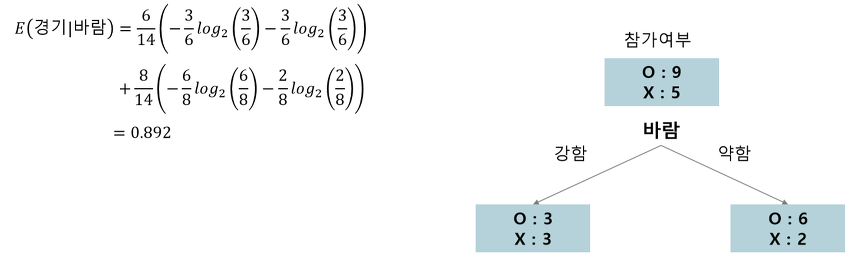
3. 각 속성에 대한 정보 획득 계산 후 정보획득이 최대가 되는 분기 조건 찾기

4. 모든 Leaf 노드의 불순도가 0이 될 때까지 반복 수행

- 최종 결과
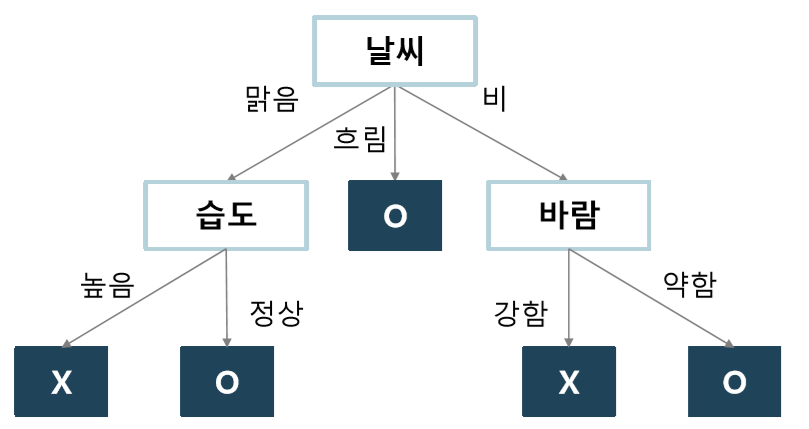
Leaf Node가 한 가지 범주만을 가지게 되는 Pure Full Tree를 형성
과적합 문제로 인해 성능 저하가 발생하기 때문에 가지치기가 필요
가지치기 (Pruning)
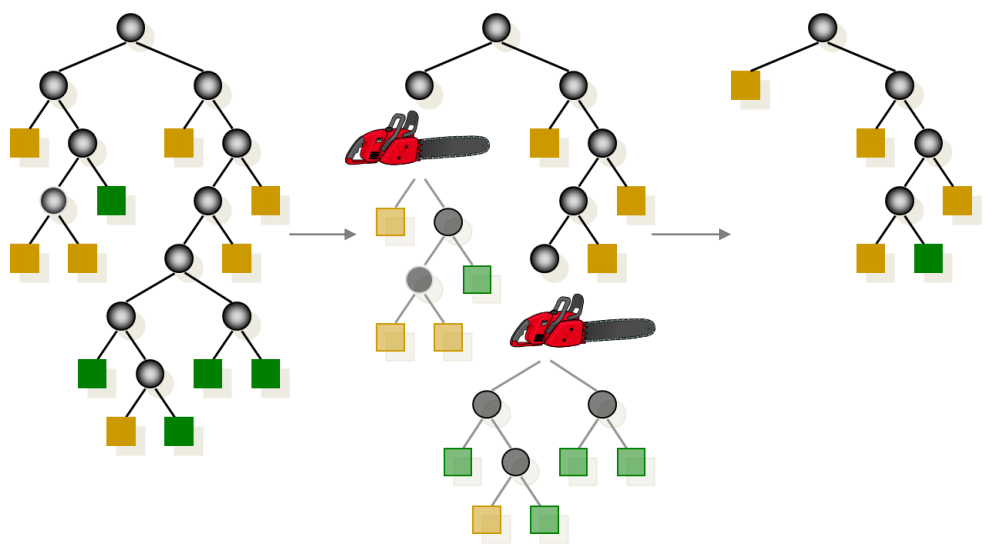
-
의사결정트리를 사용하면 Leaf Node가 한 가지 범주만을 가지게 되는 Pure Full Tree를 형성하지만 과적합 문제로 인해 성능 저하가 발생하기 때문에 가지치기가 필요
-
결정트리의 특정 노드 밑의 하부 트리를 제거하여 성능을 높이는 효과
-
: 의사결정트리의 비용 복잡도
-
: 검증데이터에 대한 오분류율
-
: 과 를 결합하는 가중치 (보통 0.01 ~ 0.1의 값)
-
: 구조의 복잡도
- 장점
- 전처리를 하지 않아도 된다.
- 수치형과 범주형 변수를 동시에 다룰 수 있다.
- 단점
- 샘플의 사이즈가 크면 효율성 및 가독성이 떨어진다.
- 한 번에 하나의 변수만을 고려하기 때문에 변수간의 상호작용 파악이 어렵다.
- 모든 단계마다 기준값의 선택이 중요하다.
- 각 예측 변수의 효과 파악이 어렵다.
