AlexNet 논문 리뷰

AI Scientist를 목표로!·2022년 11월 11일
논문 구현
0

이번에 읽었던 논문은 'ImageNet Classification with Deep Convilutional Neural Networks'(AlexNet)(2012) 입니다.

AlexNet

과거 컴퓨터 비전 분야의 올림픽이라 할 수 있는 ILSVRC의 2012 대회에서 AlexNet이 Top 5 test error 기준 15.4%를 기록해 2위(26.2%)를 따돌리고 1위를 차지하면 인기가 많아졌습니다.

당시 AlexNet 덕분에 CNN이 주목을 받으며 CNN구조의 GPU구현과 Dropout 적용이 보편화 되었습니다.

모델 구조도

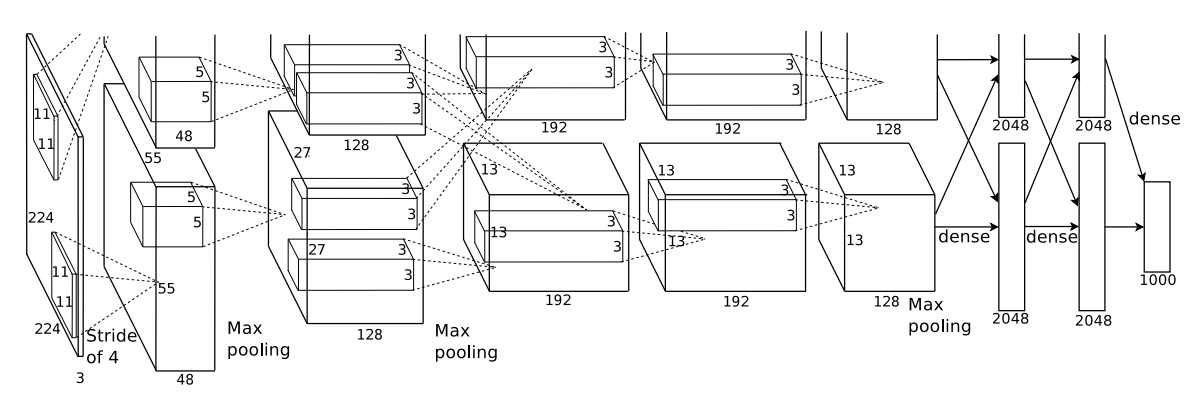
주요 특징

ReLU Non-linearity

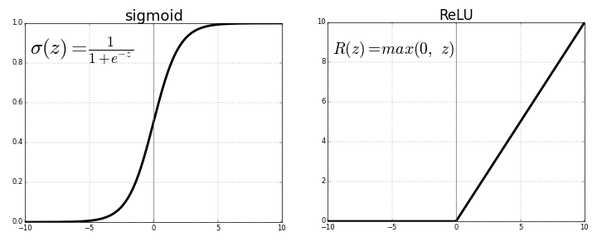
  • AledNet 이전 모델들의 활성화 함수는 주로 Sigmoid, tanh를 사용했지만 AlexNet에서는 ReLU를 사용
  • ReLU는 x값이 양수일 경우 기울기가 일정하기 때문에 gradient vanishing 현상이 일어나지 않고, 연산 비용이 비교적 적다
  • 실제로 CIFAR-10을 가지고 비교한 결과 25% training error rate에 도달하는 시간이 6배 가량 빠르다

딥러닝에서 비선형 함수를 사용해야 하는 이유

Training on Multiple GPUs

  • 더 큰 네트워크를 위해 GPU 2개를 병렬로 연산
  • 3번째 Conv Layer와 FC Layer를 제외하고 독립적으로 훈련 진행
  • GPU 1개 사용과 비교해 Training Error를 1~2% 가량 감소 및 시간 단축

Local Responese Normalization

논문에 따르면 "ReLU는 sigmoid형 함수와는 달리 input normalization이 필수는 아니다. 하지만 AlexNet에서는 local response normalization를 적용해 오차를 약 1~2% 줄였다"고 합니다.

Local Responese Normalization이란 무엇일까요?

LRN은 측면 억제를 위한 Layer입니다.

측면억제란 "신경 생리학 용어로, 한 영역에 있는 신경 세포가 상호 간 연결 되어 있을 때 그 자신의 축색이나 자신과 이웃 신경 세포를 매개하는 중간신경세포를 통해 이웃에 있는 신경 세포를 억제하려는 경향" 이라고 정의합니다.

네 너무 어렵습니다...

아래 그림은 측면억제의 대표적인 그림인 헤르만 격자 입니다.

헤르만 격자는 검은색 사격형과 사격형 사이의 흰색 줄로 이루어진 그림입니다.

하지만 그림을 보다보면 흰색 줄이 이어진 부분에 회색으로 점이 등장하게 됩니다.

흰색 선이 교차하는 점을 인식하는 망막 신경절 세포가 흰색 선을 인식하는 세포보다 억제된 신호를 보내기 때문에 회색 점이 보이는 것 입니다.

즉, 측면 억제로 인해 회색 점이 보이게 되는 것이죠

AlexNet에서 측면 억제를 왜 사용했을까?

AlexNet의 활성화 함수는 ReLU 입니다.

ReLU는 음수는 0으로, 양수는 양수 그대로를 사용합니다.

여기서 집중할 점은 양수는 양수 그대로의 값을 사용한다는 점 입니다.

만일 큰 양수의 수가 Conv Layer or MaxPooling시 들어오게 된다면 하나의 큰 값이 주변에 값에 영향을 미치게 될 것 입니다.

AlexNet에서는 이러한 부분을 방지하기 위해서 사용하게 되었다고 합니다.

Overlapping Pooling

  • 전통적으로 Pooling은 Unit의 크기와 Stride의 크기가 같아 격자와 같이 나뉜다.
  • AlexNet의 경우 Kernel_size(=3)를 Stride(=2)보다 크게 사용해 Overlap 되게 사용

Data Augmentation

  • 과적합을 방지하기 위한 가장 쉬운 방법 중 하나는 Label-preserving Transformation(라벨 보존 변형)을 사용해 Dataset을 늘리는 것
  1. generating image translation and horizontal reflections

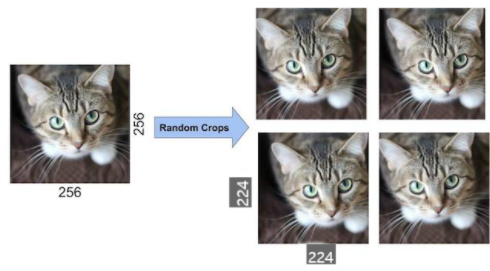
  • (256 x 256)의 이미지를 (224 x 224)로 중앙, 좌상단, 좌하단, 우상단, 우하단 5가지로 Crop
  • Horizontal Reflection으로 하나의 이미지를 10개로 증강
  1. altering the intensities of the RGB channels in training images
  • RGB Pixel 값에 대한 PCA를 적용해 각 색상에 대한 Eigenvalue를 찾아 평균 = 0, 분산 = 0.1인 가우시안 분포에 추출한 랜덤 변수를 곱해 RGB 값에 더해줌

Dropout

-Dropout은 히든 레이어의 특정 뉴런의 출력을 일정 확률로 0으로 만드는 것

  • 불확실성을 부여해 특정 뉴런에 의존하지 못하도록 하는 것으로 과적합을 감소

Code 구현

저는 FashionMNIST를 통해 AlexNet을 구현해 보았습니다.
기존 AlexNet의 Input은 (3 X 227 X 277) 이지만
FashionMNIST의 특성상 Input 값을 (1 X 227 X 277)로 하였습니다.

  • Trnasform.compose
transform = transforms.Compose([
    transforms.Resize(227), # 논문에서 input 이미지 사이즈 (227 X 227)
                           # FashionMNIST의 사이즈는 (28 X 28) 이기 때문에 변형 필요
    transforms.ToTensor(), # PLT image or Numpy.ndarray를 torch.FloatTensor로 변환
    transforms.Normalize((0.5),(0.5))  # 데이터 정규화 Why? 데이터 가져오기 및 훈련을 빠르게 만드는데 도움
                                       # FashionMNIST의 경우 Gray scale 값만 가지므로 0.5만 설정                       
    ])
  • Dataset
root = '/content/drive/MyDrive/논문/AlexNet'

train_data = datasets.FashionMNIST(
    root = root,              # data가 저장될 경로
    train = True,             # train dataset으로 사용
    download = True,          # 데이터 다운로드
    transform = transform    # Feature 및 label 변환
)

test_data = datasets.FashionMNIST(
    root = root,
    train = False,
    download = True,
    transform = transform
)


# Fashion MNIST는 10개의 카테고리 존재

class_names = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat',
               'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot'] # 총 10개의 클래스
  • DataLoader
train_loader = DataLoader(train_data, batch_size=64, shuffle=True, drop_last = True, pin_memory = True,num_workers=3)
                                                                                  # Tensor를 CPU -> GPU로 올림
test_loader = DataLoader(test_data, batch_size=64, shuffle=True, drop_last = False, pin_memory = True,num_workers=3)
  • AlexNet

class AlexNet(nn.Module):
  def __init__(self):
    super().__init__()
    self.conv1 = nn.Sequential(
                      nn.Conv2d(in_channels = 1, out_channels = 96, kernel_size = 11, stride = 4, padding = 0),
                          # input_size = (B X 1 X 277 X 277)  --> 논문에서는 (3 X 277 X 277)이나 FashionMINIST 특성상 1로 수정
                          # outpur_Size = (B X 96 X 55 X 55)
                      nn.ReLU(),
                      nn.LocalResponseNorm(size=5, alpha=0.0001, beta=0.75, k=2),  # LRN
                      nn.MaxPool2d(kernel_size = 3, stride = 2)
                          # 55 -> (55+2*0-3)/2 + 1 => 27 
                          # output_size = (B X 96 X 27 X 27)
                      )
    self.conv2 = nn.Sequential(
                      nn.Conv2d(in_channels = 96, out_channels = 256, kernel_size = 5, stride = 1, padding = 2),
                          # input_size = (B X 96 X 27 X 27)
                          # output_size = (B X 256 X 27 X 27)
                      nn.ReLU(),
                      nn.LocalResponseNorm(size=5, alpha=0.0001, beta=0.75, k=2),  # LRN
                      nn.MaxPool2d(kernel_size = 3, stride = 2)
                          # input_size = (B X 256 X 27 X 27)
                          # output_size = (B X 256 X 13 X 13)
                      )
    self.conv3 = nn.Sequential(
                      nn.Conv2d(256, 384, 3, 1, 1),   # --> (B X 384 X 13 X 13)
                      nn.ReLU()                       
                      )
    self.conv4 = nn.Sequential(
                      nn.Conv2d(384, 384, 3, 1, 1),   # --> (B X 384 X 13 X 13)
                      nn.ReLU()                       
                      )
    self.conv5 = nn.Sequential(
                      nn.Conv2d(384, 256, 3, 1, 1),   # --> (B X 256 X 13 X 13)
                      nn.ReLU(),                       
                      nn.MaxPool2d(3,2)              # --> (B X 256 X 6 X 6)
                      )

    self.fclayer = nn.Sequential(
                      ########## FC1 ##########
                      nn.Linear(256 * 6 * 6, 4096),
                      nn.Dropout (p = 0.5, inplace = True),
                      nn.ReLU(),
                      ########## FC2 ##########
                      nn.Linear(4096, 4096),
                      nn.Dropout (p = 0.5, inplace = True),
                      nn.ReLU(),
                      ########## FC3 ##########
                      nn.Linear(4096, 10)   # 논문은 1000개 Class 지만 FashionMINIST는 10개 Class
                      )
    self.init_weight()



# 각 layer에 대해 평균이 0이고 표준편차가 0.01인 가우시안 분포로 가중치를 초기화
  def init_weight(self):
    for layer in [self.conv1, self.conv2, self.conv3, self.conv4, self.conv5]:
      if isinstance(layer, nn.Conv2d):
        nn.init.normal_(layer.weight, mean=0, std=0.01)
        nn.init.constant_(layer.bias, 0)


    # 2,4,5번째 합성곱 계층과 완전연결계층의 편향(biases)을 상수 1로 초기화
    nn.init.constant_(self.conv2[0].bias, 1)
    nn.init.constant_(self.conv4[0].bias, 1)
    nn.init.constant_(self.conv5[0].bias, 1)

    nn.init.constant_(self.fclayer[0].bias, 1)
    nn.init.constant_(self.fclayer[3].bias, 1)
    nn.init.constant_(self.fclayer[6].bias, 1)

  def forward(self, x):
    out = self.conv1(x)
    out = self.conv2(out)
    out = self.conv3(out)
    out = self.conv4(out)
    out = self.conv5(out)
    out = out.view(out.size(0), -1) # 64x4096
    out = self.fclayer(out)
    return out
  • Model 학습
num_epochs = 10

train_acc_history = []
train_loss_history = []
test_acc_history = []
test_loss_history = []

for epoch in range(num_epochs):
  # 모델 훈련모드 설정
  train_accuracy = 0
  
  model.train()
  for batch_idx, (data, target) in enumerate(tqdm(train_loader)):
    
    # Gradient 초기화
    optimizer.zero_grad()
    
    # data, target을 device에 올림
    target = target.type(torch.LongTensor)
    data, target = data.to(device), target.to(device)


    # Forward_propagation
    output = model(data)

    ############################# Loss #############################
    # 손실함수를 통해 Loss 계산
    loss = criterion(output, target)

    # Backward_propagation
    loss.backward()
    ################################################################

    # 수정된 Gradient 업데이트
    optimizer.step()

    ############################# Accuracy #############################
    # max probability와 max index를 반환
    # max probability는 무시하고, max index는 pred에 저장하여 label 값과 대조하여 정확도를 도출
    _, preds = torch.max(output,1)
    train_accuracy += torch.sum(preds == target)
    ####################################################################
    
    train_loss_history.append(loss.item())
    train_acc_history.append(train_accuracy.item() / len(train_loader.dataset))

    if (batch_idx + 1) % 300 == 0:
      print(f"epoch : {epoch + 1}, Loss : {loss.item():.3f}, Accuracy : {train_accuracy.item() / len(train_loader.dataset):.3f}")
  print('='*70)
  print(f"epoch : {epoch + 1}, train_Accuracy : {train_accuracy.item() / len(train_loader.dataset):0.3f}")
  print('='*70)

  model.eval()

  test_loss = 0
  test_accuracy = 0

  with torch.no_grad():
    for batch_idx, (data, target) in enumerate(tqdm(test_loader)):
    
      # data, target을 device에 올림
      target = target.type(torch.LongTensor)
      data, target = data.to(device), target.to(device)

      # Forward_propagation
      output = model(data)

      # 손실함수를 통해 Loss 계산
      test_loss += criterion(output, target).item() * data.size(0)

      ############################# Accuracy #############################
      # max probability와 max index를 반환
      # max probability는 무시하고, max index는 pred에 저장하여 label 값과 대조하여 정확도를 도출
      _, preds = torch.max(output,1)
      test_accuracy += torch.sum(preds == target)
      ####################################################################
      
      test_loss_history.append(test_loss / len(test_loader.dataset))
      test_acc_history.append(test_accuracy.item() / len(test_loader.dataset))

  print(f"epoch : {epoch + 1}, Loss : {test_loss / len(test_loader.dataset) :0.3f}, Accuracy : {test_accuracy.item() / len(test_loader.dataset) :.3f}")
profile
AI Scientist를 목표로!
딥러닝 지식의 백지에서 깜지까지
이전 포스트

딥러닝에서 비선형 활성화 함수를 사용하는 이유?

다음 포스트

1. 추천 시스템의 이해 (by Tacademy)

0개의 댓글