Encoder의 두 개의 서브층에 대해서 이전에 설명하였습니다.

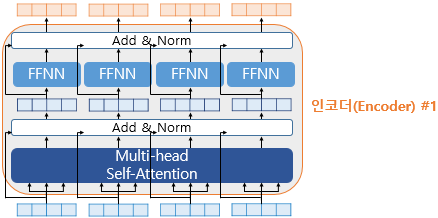
2개의 서브층을 가진 Encoder에 추가적으로 사용하는 기법은 잔차 연결(Resicdual connection)과 층 정규화 (Layer normalization) 이며 위 그림에서는 Add & Norm로 표시되어 있습니다.

---

잔차 연결 (Residual connection)

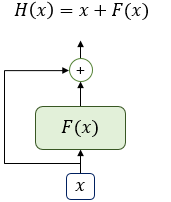
위 그림은 입력 $x$와 함수 $F(x)$의 값을 더한 함수 $H(x)$의 구조를 보이고 있습니다.

여기서 함수 $F(x)$는 Transformer에서의 서브층에 해당이 됩니다.

그림에 보이듯이 잔차연결은 서브층의 입력과 출력을 더하는 것 입니다.

Transformer에서는 행렬의 연산으로 multi-head Attention, FFNN 등을 구하고 마지막에 가중치값인 W값을 구해서 입력값과 출력값을 동일한 차원을 가지게 만들고 있습니다.

그로인해, 잔차 연결에서는 입력값과 출력값이 동일한 차원을 가지고 있어 더하기(+)연산이 가능하게 됩니다.

식으로 표현한다면 $x + sublayer(x)$입니다.

서브층이 Multi-head Attention이었다면 아래의 수식과 같습니다.

				H(x) = x + Multi - head Attention (x)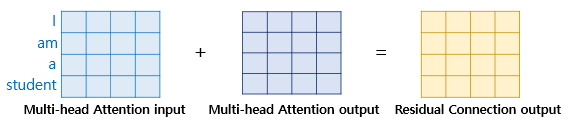

만일 서브층이 Multi-head Attention이었다면, 잔차 연결은 위 그림과 같을 것 입니다.

---

층 정규화 (Layer normalization)

잔차 연결을 거친 후 이어서 층 정규화 과정을 거치게 됩니다.

잔차 연결의 입력값을 x, 잔차 연결과 층 정규화를 모두 거친 결과 값을 LN이라고 할 경우, 잔차 연결 후 층 정규화 연산을 수식으로 표현하면 다음과 같습니다.

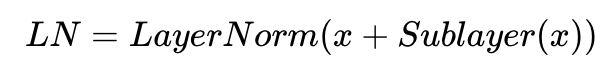
층 정규화는 Tensor의 마지막 차원에 대해서 평균과 분산을 구하고, 이를 가지고 어떤 수식을 통해 값을 정규화 하여 학습에 도움을 주게 됩니다.

Tensor의 마지막 차원이라는 것은 Transformer의 $d_{model}$차원을 의미합니다.

아래 그림은 $d_{model}$의 차원의 방향을 화살표로 표현하였습니다.

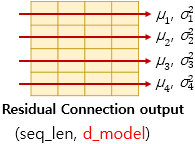
층 정규화를 위해 먼저 화살표 방향으로 각각 평균 $u$과 분산 $σ^2$을 구합니다.
여기서 각 화살표의 방향의 벡터를 $x_i$라고 칭해보겠습니다.

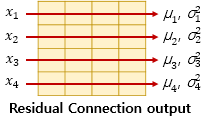
층 정규화를 수행한 후에 벡터 $x_i$는 $ln_i$ 벡터로 정규화가 됩니다.

수식으로 표현하자면 $ln_i = LayerNorm(x_i)$ 과 같습니다.

층 정규화를 2가지 과정으로 나누어 설명하도록 하겠습니다.

1. 평균과 분산을 통한 정규화
2. 감마와 베타를 도입

우선, 평균과 분산을 통해 벡터 $x_i$를 정규화 해줍니다. $x_i$는 벡터, 평균 $u_i$, 분산 $σ^2$는 스칼라 값 입니다.

스칼라: 특정한 하나의 수치, 단위로 표현되며 방향은 없다
벡터: 특정한 하나의 수치, 단위 그리고 방향으로 포현된다.

벡터 $x_i$의 각 차원을 $k$라고 하였을 때, $x_{i,k}$는 아래의 수식과 같이 정규화 될 수 있습니다.

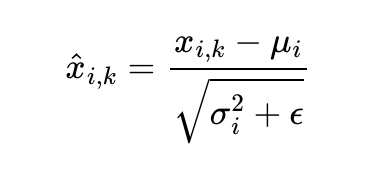
다시말해, 벡터 $x_i$의 각 $k$ 차원의 값이 정규화가 되는 것 입니다.

위 수식에서 ε(입실론)은 분모가 0이 되는 것을 방지하는 값입니다.

이후 γ(감마)와 β(베타)라는 벡터가 등장하며 이들의 초기값은 각각 1과 0입니다.

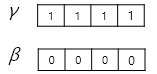
γ(감마)와 β(베타)는 학습 가능한 파라미터이며 최종 수식은 아래와 같습니다.

---

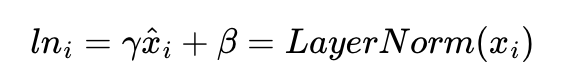
Batch Norm VS Layer Norm

Batch Normalization 과 Layer normalization 모두 차이나는 정도를 줄이기 위해 사용되나, 그 방향이 서로 다르다는 차이점이 있다.

• BN은 각 Feature의 평균과 분산을 구해 batch에 있는 각 Feature를 정규화 한다.

• LN은 각 input의 Feature들에 대한 평균과 분산을 구해 batch에 있는 각 input을 정규화 한다.

어렵풋이 보면 이해하기 어렵고 비슷비슷한 느낌이 듭니다.

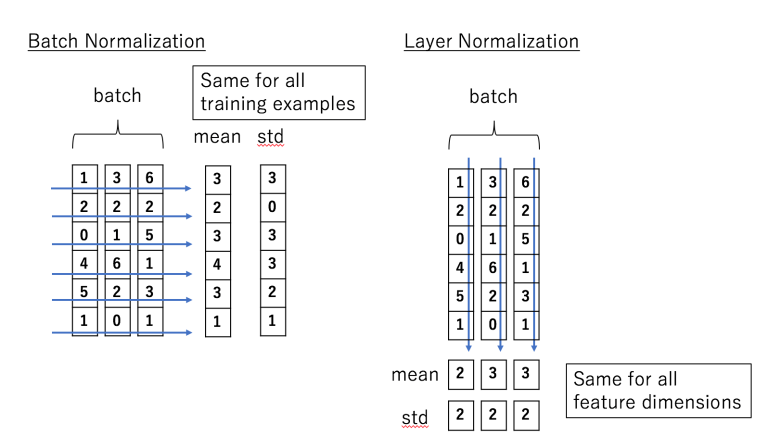
위 그림을 보면 BN은 특성(Feature) 단위로 평균(mean)과 표준편차(std)를 계산하여 정규화 합니다.

즉, Feature의 개수가 6개 이기 때문에 각각 6개의 평균과 표준편차를 계산하고 정규화 하게 됩니다.

하지만 LN의 경우, 데이터의 Sample 단위로 평균(mean)과 표준편차(std)를 계산해서 정규화를 합니다.

다시말하자면, Feature의 개수와는 상관없이 batch안에 데이터 Sample의 수가 3개이기 때문에 3개의 평균과 표준편차를 계산하게 되는 것 입니다.

• BN은 Batch Size에 걸쳐서 처리되므로 Batch Size와 관련이 깊지만,

• LN은 각 input(=Sample)에 대해서만 처리되므로 Batch Size와는 전혀 상관이 없게 됩니다.

---

Transformer에서는 왜 Layer Norm을 사용했을까?

기존 BN의 단점은 아래와 같습니다.

• Mini-Batch 크기에 의존적이다
  • 만약 Mini-Batch가 1일 경우 분산이 없기 때문에 Normalizing이 안되게 됩니다.
• Recurrent(순환 신경망) 기반의 모델에 적용이 어렵다
  • 기존 Feed-Forward 형태의 신경망에는 각 배치별 입력의 형태가 동일하기 때문에 Normalization에 문제가 없다.
  • 하지만, Recurrent 기반의 모델의 입력값은 기본적으로 Sequence이기 때문에 매 time-step 마다 별도의 통계량(평균,분산)을 저장해야 해서 모델의 복잡도가 증가하게 된다.

하지만 LN은 위에서 언급했듯이 batch 단위가 아닌 input 단위로 평균과 분산을 계산하기 때문에 아래와 같은 특징을 가지게 됩니다.

• 데이터 마다 각각 다른 Normalization Term($u$,$σ$)을 갖는다.

• Mini-batch의 크기에 영향을 받지 않는다.

• 서로 다른 길이를 갖는 Sequence가 batch 단위로 들어오는 경우에도 각각 다른 Normalization Term을 가지기 때문에 적용이 가능하다.

또한 RNN 모델에서 많은 Time-Step을 거칠 때, Gradient Explode or Vanish 현상이 발생하게 되는데

LM을 적용한다면, Layer의 input이 scale에 영향을 받지 않기 때문에 안정적인 학습이 진행된다고 합니다.