플로이드-워셜 알고리즘 이란?

• 특정 지점까지 가장 빠르게 도달할 수 있는 경로를 찾는 알고리즘

• 길찾기 알고리즘으로도 불림

• 모든 노드 간의 최단 경로를 계산할 때 사용하는 알고리즘

• 노드의 개수가 N개 일때, 각 동작 단계별로 노드 1개씩을 선택하기 때문에 동작 단계는 총 N 개

• 현재 노드를 제외하고 N - 1 개의 노드 중에서 서로 다른 2개의 노드로 구성된 한 쌍을 선택하고 최단 경로를 계산하는 방식

---

특징

• 모든 노드별로 특정 노드를 거쳐 다른 모든 노드로 가는 최단 경로를 저장하기 위해 2차원 리스트를 활용한다. 따라서 노드의 개수가 N개 라면, 전체 시간 복잡도는 $O(N^3)$

• 시작 노드가 1개가 아닌 다수 즉, 모든 노드에서 모든 노드까지의 최단거리를 구하는 방법

• 즉, 노드의 개수가 적다면 플로이드-워셜 알고리즘을 사용하는 것이 효과적

• 반대로, 노드와 간선의 개수가 많을 경우 다익스트라 알고리즘을 사용하는 것이 더 효과적

• 다익스트라 알고리즘과는 다르게 가중치가 음수일 경우에도 사용이 가능

• 시작정점(s), 도착정점(e), 경유하는 정점(t)을 활용해 최단거리를 구함

• 다시말하면 시작정점(s)과 도착정점(e) 간의 최단거리는 시작정점(s)과 경유하는 정점(t) 사이의 최단거리 + 도착정점(e)과 경유하는 정점(t) 간의 최단거리

• dist[s][e] = dist[s][t] + dist[t][e]

---

동작 과정

1. 하나의 정점에서 다른 정점으로 바로 갈 수 있는 경우 최소 비용을, 갈 수 없다면 inf로 배열에 값을 저장

2. 3중 for문을 통해 거쳐가는 정점을 설정한 후 해당 정점을 거쳐가서 비용이 줄어드는 경우 값을 변경

3. 위 과정을 반복해 모든 정점 사이의 최단 경로를 탐색

---

• 6개의 정점과 9개의 간선과 거리 비용으로 이루어진 그래프와 표

경유정점이 1번일 경우

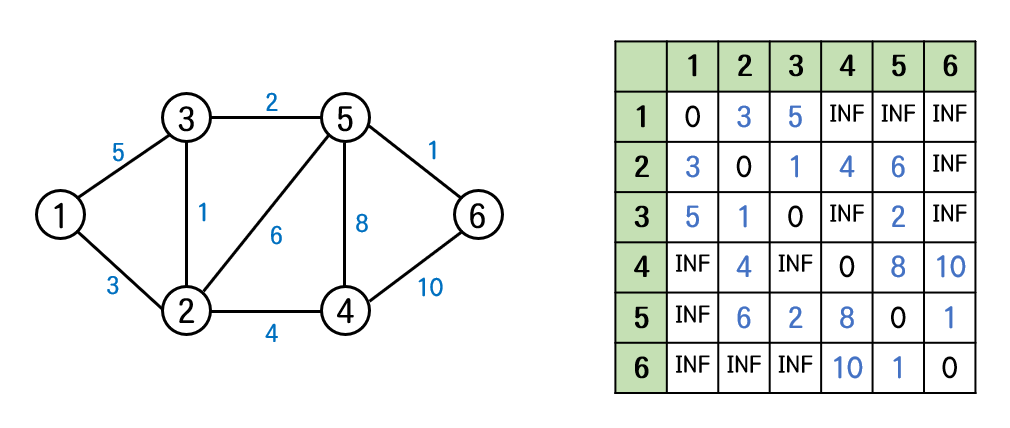
• dist[1][1] : dist[1][1] + dist[1][1] = 0 + 0 = 0 -> dist[1][1]의 초기값 0보다 크기 않으므로 갱신X

• dist[1][2] : dist[1][1] + dist[1][2] = 0 + 3 = 3 -> dist[1][2]의 초기값 3보다 크기 않으므로 갱신X

• dist[1][3] : dist[1][1] + dist[1][3] = 0 + 5 = 10 -> dist[1][3]의 초기값 5보다 크기 않으므로 갱신X

• dist[1][4] : dist[1][1] + dist[1][4] = 0 + INF = INF -> dist[1][4]의 초기값 INF보다 크기 않으므로 갱신X

• dist[1][5] : dist[1][1] + dist[1][5] = 0 + INF = INF -> dist[1][5]의 초기값 INF보다 크기 않으므로 갱신X

• dist[1][6] : dist[1][1] + dist[1][6] = 0 + INF = INF -> dist[1][6]의 초기값 INF보다 크기 않으므로 갱신X

경유정점이 2번일 경우

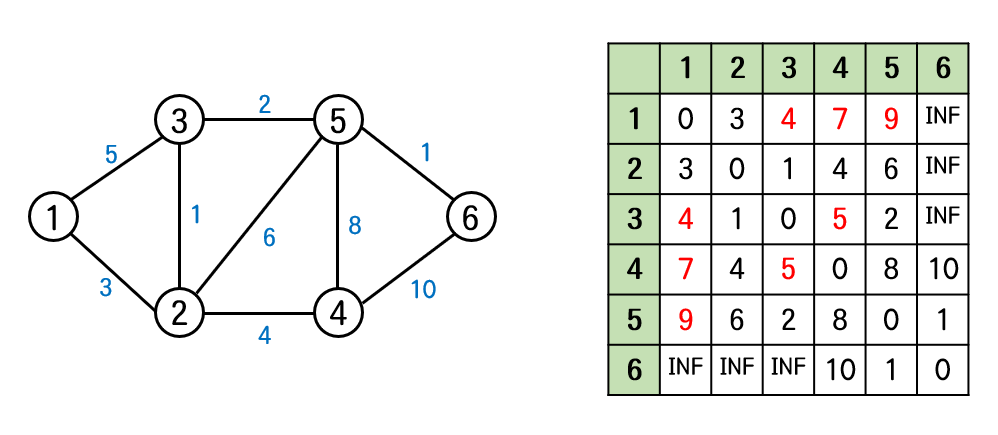
• dist[1][1] : dist[1][2] + dist[2][1] = 3 + 3 = 6

• dist[1][2] : dist[1][2] + dist[2][2] = 3 + 0 = 3

• dist[1][3] : dist[1][2] + dist[2][3] = 3 + 1 = 4 -> dist[1][3] = 5보다 크므로 갱신! dist[1][3] = 4

• dist[1][4] : dist[1][2] + dist[2][4] = 3 + 4 = 7 -> dist[1][4] = INF보다 크므로 갱신! dist[1][4] = 7

• dist[1][5] : dist[1][2] + dist[2][5] = 3 + 6 = 9 -> dist[1][5] = INF보다 크므로 갱신! dist[1][5] = 9

• dist[1][6] : dist[1][2] + dist[2][6] = 3 + INF = INF

과정을 모두 반복했을 경우

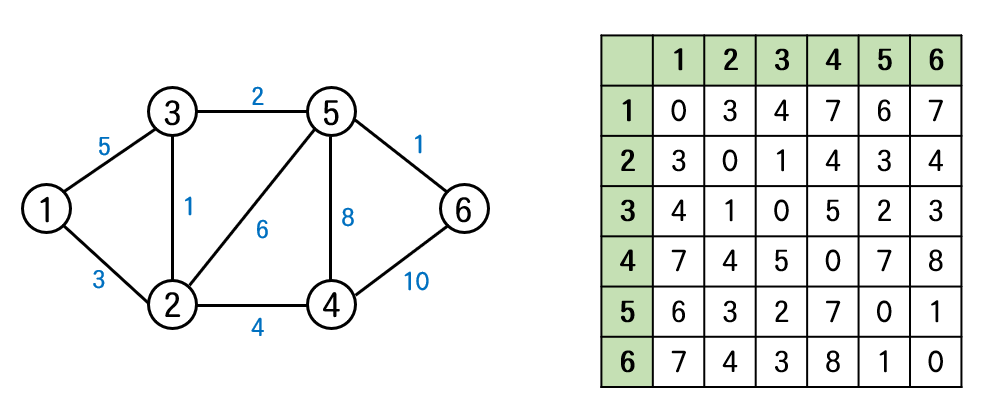
• 모든 시작점과 끝점 경유점을 다 돌고 난 후에 표를 최단거리값이 갱신이 된다.

---

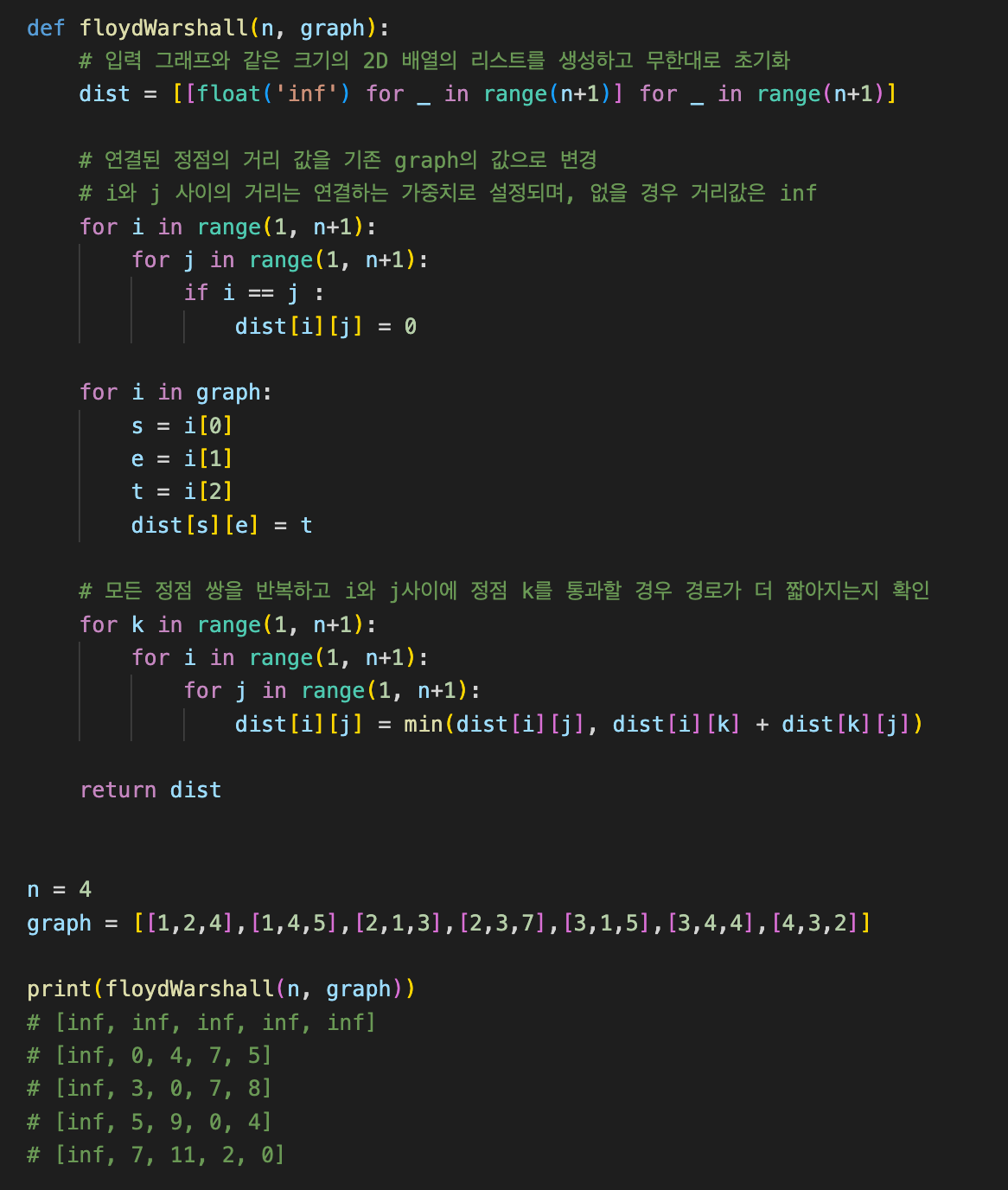
Code