코딩테스트 하면서, 고민을 많이했거나 못풀었거나 혹은 추후에 다시 볼만한 문제를 골라서만 기록하려고 한다.
프로그래머스 2단계 연습문제
https://school.programmers.co.kr/learn/courses/30/lessons/148652
문제이해
- 처음 문제를 읽을 때는 이게 무슨 말이지? 라는 생각이 들어서, 문제를 다시 하나하나 정독해가면서 다시 보니 아래와 같았다.
- 주어지는 수는 n ,l , r 인데,
- n의 경우 : 1번째, 2번째.. n번째 문자열(유사 칸토어 비트열)를 가르킨다.
- l의 경우 : left의 줄인 말로, 시작점을 말한다.
- r의 경우 : right의 줄인 말로 끝지점을 말한다.
- 문제는 l에서 부터 r까지의 범위안에서
1의 갯수가 몇개인지 구하는 문제이다.그럼 유사칸토어 비트열이 무엇일까?
유사 칸토어 비트열
- 0번째 유사칸토어 비트(문자)열 : "1" 이다.
- 1번째 유사칸토어 비트(문자)열열 : "11011" 이다.
- 2번째 유사칸토어 비트(문자)열열 : "1101111011000001101111011" 이다.
-
즉, 번째가 증가할 수록,
1->"11011" ,0->"00000" 로 변하면서 늘어 나는 비트열을 말한다. -
그래서 문자열의 길이도
1→ 5→ 25→ 125로 규칙적으로 늘어난다.
제한사항
- n의 범위는 1부터 20까지임을 알 수 있고, 자연스레
l,r의 값 범위도 5^n이 된다. - 다만, 여기서 궁금한 건
l+ 10,000,000 의 의미는 뭘까?

첫번째 풀이
- 유사 칸토어 비트열의 규칙이 생긴다.
- 이전 비트열보다 무조건 5배의 길이 만큼 늘어나고, 총 5영역이라고 했을때, 아래와 같다.
[이전 비트열][이전 비트열] [0밖에 없는 존][이전 비트열][이전 비트열]- 한 구역에 있을 1의 갯수는 4^(n-1)개 이다.
- 이 커다란 범위안에서,
l~r까지 사이의 1의 갯수- 이전 비트열의 길이를 제기위해, 5^(n-1) 을 계산한다. 범위가 큼으로
long type - l /len = 나온값, r/len = 나온값을 비교한다. ⇒ 5개의 영역 중 에 한곳
- “3영역”이면 0이기에 제외한다.
- l %len = l값, r%len = r값을 계산한다. ⇒0이 아니라면, 또다시 5등분으로 나눈다.
- 이전 비트열의 길이를 제기위해, 5^(n-1) 을 계산한다. 범위가 큼으로
- 한 구역당 길이는 5^(n-2)개 이며, 1의 갯수는 4^(n-2)개, 단 3구역 제외
- l값의 경우, l값1/len = 나온값 ,
- r값의 경우, r값1/len = 나온값
시행착오를 겪어봤지만, 실패했다.
그림으로 그려보기
- 그래서 이번에는 좀 더 문제를 이해하고 쉽게 풀어보고자 그림을 그려봤다.
- 일단 예시로
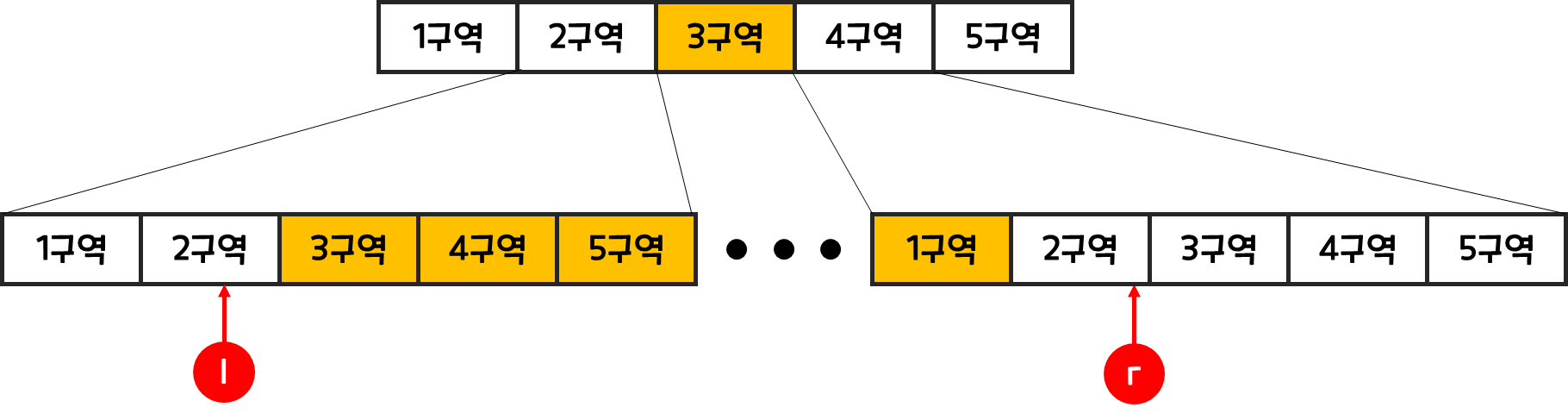
l은 2구역에,r은 4구역에 있다고 가정하자 - 각 구역에 해당하는 l과 r 은 정확히 어디에 위치하는 지는 모르지만, 3구역은 무조건 포함하고 있으니, 해당 부분을 계산해 주면된다.
- 그리고 각각의 2,4 구역은 구간은 또 다시 5개의 구역으로 나눌 수 있다.

- 이때 왼쪽은
l로 시작하고, 5구역 끝에서 끝나야한다. - 반대쪽인 오른쪽은 1구역에서 시작해야되고,
r에서 끝나야 한다.- 재귀함수를 사용해야함을 여기서 느꼈다.
하지만, 다른 경우도 있을 수 있으니 검증해보자.
- 이번엔
l과r이 같은 구역에 있는 경우이다.
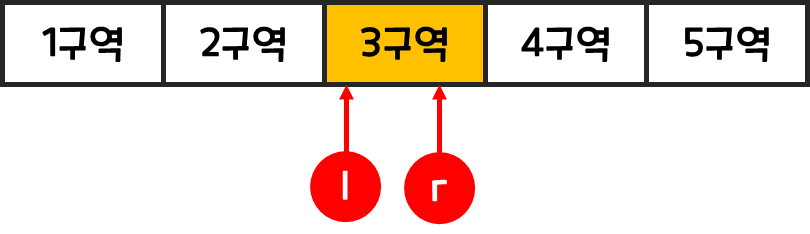
- 경우는 두가지가 나올 수 있는데,
- 하나는 5분할했을때,l과r이 다른 구간에 있어 나눠지는 경우,
- 다른 하나는 또다시 같은 구역에 있는 경우이다.
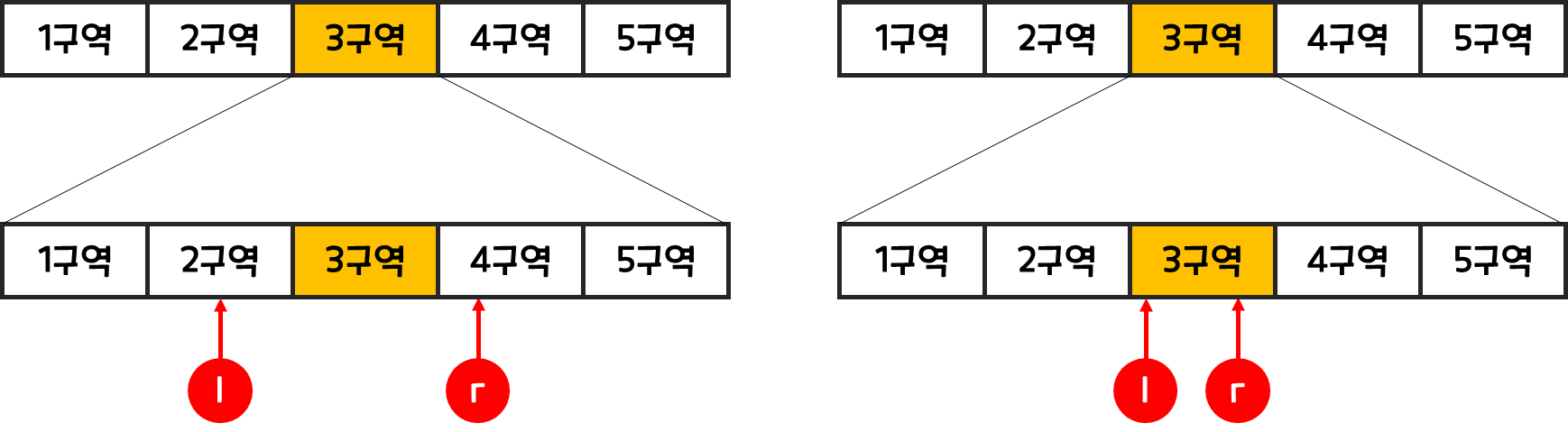
-
이둘은 이미 위에서 언급했던 2가지 경우가 반복되는 것이다보니, 이것을 이용하여 풀 수 있을 것같다.
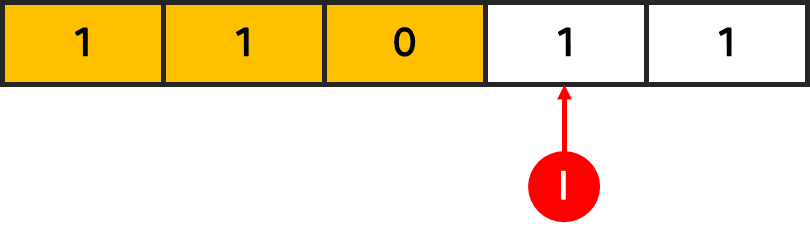
-
그리고 마지막의 경우는 본인위치를 제외한 나머지의 1의 갯수를 계산했기 때문에,
l과r의 위치가 1인지 0 인지 만 확인하여 추가해주면 된다.
다시 풀이
- 함수에 어떤것이 필요할까?
- void dfs(areaLength, countOne , start, end)
- start / areaLength 으로 시작 지점 구역 알아내기
- end / areaLength 로 끝지점 구역 알아내기
- 중간 지역이 존재하면 countOne 만큼 더해줌
- 재귀로 2개로 나누어 진행
- dfs(areaLength/5 ,countOne /4 , start, start구역 끝부분)
- dfs(areaLength/5 ,countOne /4 , end 구역 시작부분 , end)
- 만약 중간 지역이 존재하지않는다면, 한번더 재귀를 통해준다.
- dfs(areaLength/5 ,countOne /4 , start, end)
- 그리고 마지막으로 l과 r의 위치 값이 1이면 각각 +1 씩해주고 리턴한다.
작성코드
class Solution {
int answer;
public int solution(int n, long l, long r) {
answer = 0;
long areaLength = 1;
int countOne =1;
while(n>1){
areaLength *= 5L;
countOne *= 4;
n--;
}
dfs(areaLength, countOne, l,r);
return answer;
}
private void dfs(long areaLength, int countOne, long start, long end){
if(areaLength == 1L){
long c = end - start + 1;
if(c >= 3 || end ==3 || start == 3){
c--;
}
answer +=c;
return;
}
long startArea = start / areaLength;
if(start % areaLength > 0){
startArea++;
}
long endArea = end/areaLength;
if(end % areaLength > 0) {
endArea++;
}
if(endArea > startArea){// 같은 구역이 아니면
long includArea = endArea - startArea - 1L;
if(startArea%5 < 3 && ((endArea)%5 >3 || endArea%5 == 0)){ // 3구역 포함
includArea--;
}
answer += (includArea*countOne);
if(startArea != 3) {
dfs(areaLength / 5, countOne / 4, start, startArea * areaLength);
}
if(endArea != 3){
dfs(areaLength/5 ,countOne/4, (endArea-1)*areaLength+1 , end);
}
}
else{
if(startArea == 3) return;
dfs(areaLength/5 ,countOne/4, start, end);
}
}
}결과
- 임의로 만든 테스트케이스까지 전부 통과했지만, 채점은 결국 다 통과하지 못했다.
- 접근 방법은 나쁘지않았다고 생각했는데, 생각보다 쉽지 않았다.
- 분명 내가 놓치고 있는 부분이 있는 게 있어보이는데, 추후에 다시한번 문제를 보고 풀어보고자한다.

여행 가기 전 날에도 알고리즘 문제를 푸시다니.. 대단하십니다 !!