(mathematics) sigma, permutation, combination, probability

Summarization

---

• Summation
• Permutation & Combination
• Probability

---

Contents

• 시그마 : 수열의 합을 나타낸 기호. $n$항까지의 합을 구할 때 사용
  $S_n = \sum_{i}^{n} a_i$

# 등차수열의 합
inputA1 = int(input('a1 입력 : '))
inputD = int(input('공차 입력: '))
inputN = int(input('n 입력: '))

valueN = inputA1 + (inputN - 1) * inputD
sumN = inputN * (inputA1 + valueN) / 2

print('-' * 30)
print('{}번째 항까지의 합: {}' .format(inputN, int(sumN)))
print('-' * 30)

# 등비수열의 합
inputA1 = int(input('a1 입력 : '))
inputR = int(input('공비 입력: '))
inputN = int(input('n 입력: '))

sumN = inputA1 * (inputA1 ** inputN - 1) / ( inputR - 1)

print('-' * 30)
print('{}번째 항까지의 합: {}' .format(inputN, int(sumN)))
print('-' * 30)

• 팩토리얼(Factorial) : 1부터 양의 정수 $n$까지의 정수를 모두 곱한 것

  • 방법 1. For문 사용

  inputN = int(input('n 입력: '))
  
  result = 1
  for n in range(1, inputN + 1):
      result *= n
  
  print('{}팩토리얼 : {}' .format(inputN, result))

  • 방법 2. While문 사용

  inputN = int(input('n 입력: '))
  
  result = 1 ; n = 1
  while n <= inputN:
      result *= n
      n += 1
  
  print('{} 팩토리얼: {}' .format(inputN, result))

  • 방법 3. 함수 사용

  def factorialFun(n):
      if n == 1:
          return 1
      return n * factorialFun(n - 1)
  
  inputN = int(input('n 입력: '))
  print('{} 팩토리얼: {}' .format(inputN, factorialFun(inputN)))

  • 방법 4. Math module 사용

  import math
  
  inputN = int(input('n 입력: '))
  print('{} 팩토리얼: {}' .format(inputN, math.factorial(inputN)))

• 군 수열 : 여러 개의 항을 묶었을 때 규칙성을 가지는 수열

• 순열 : 일렬로 나열하는 경우의 수
  • $n$개에서 $r$개를 택하여 나열하는 경우의 수
    $_n p_r = n(n-1)(n-2)\cdots(n-r+1)$

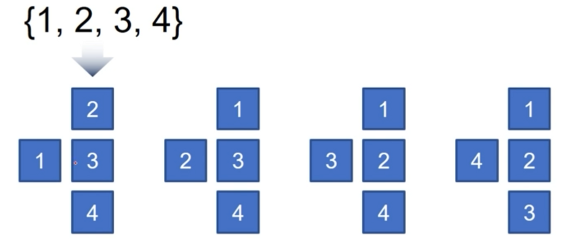
• 원순열 : 시작과 끝의 구분이 없는 순열
  $\frac{n!}{n} \qquad \text{or} \qquad (n-1)!$

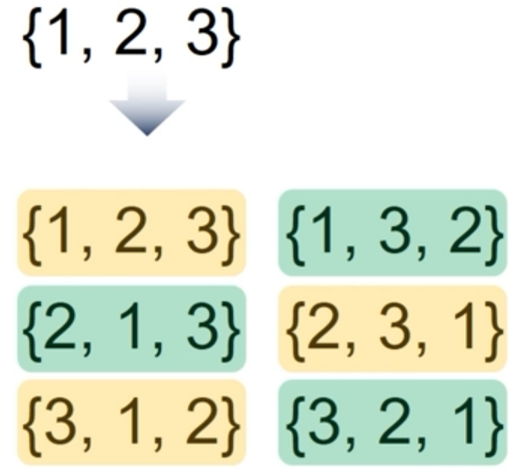
• 조합 : $n$개에서 $r$개를 택하는 경우의 수
  ※ 순열과의 차이점 : 순열은 순서가 중요!
  $_nC_r = \frac{_nP_r}{r!}$
• 확률 : 모든 사건에서 특정 사건이 일어날 수 있는 수를 나타낸 것
  • 모든 사건을 Sample space, 특정 사건은 Event라고도 함
  • 조합을 이용해 확률을 알아낼 수 있다.

# 조합
def proFun():
    numN = int(input('numN 입력: '))
    numR = int(input('numR 입력: '))
    resultP = 1 ; resultR = 1 ; resultC = 1

    for n in range(numN, (numN - numR), -1):
        resultP *= n
    print('resultP : {}' .format(resultP))

    for n in range(numR, 0, -1):
        resultR *= n
    print('resultR : {}' .format(resultR))

    resultC = int(resultP / resultR)
    print('resultC : {}' .format(resultC))

    return resultC

sample = proFun()
print('sample : {}' .format(sample))

event1 = proFun()
print('event1 : {}' .format(event1))

event2 = proFun()
print('event2 : {}' .format(event2))

# 확률
probability = (event1 * event2) / sample
print('probability : {}%' .format(round(probability * 100, 2)))