Logistic Regression

1. Multi-Class Classification

1) 문제

타깃 데이터에 3개 이상의 클래스가 포함되어 있는 분류 문제를 Multi-Class Classification(다중 분류)이라고 한다. 사실 다중 분류라 할지라도, 지난 포스팅에서 배운 이진 분류와 크게 다르지 않기 때문에 바로 관련 문제를 풀어보기로 하겠다.

랜덤 박스에 임의의 생선을 넣어 판매하려는 상황을 가정해보자. 이 랜덤 박스는 아래의 조건을 만족해야 한다.

• 랜덤 박스에는 그 안에 들어있는 생선의 종류에 대한 확률이 표시되어 있다.
• 랜덤 박스 안에 들어갈 수 있는 생선의 종류는 총 7개로, 7개의 생선에 대한 확률이 모두 표시되어야 한다.
• 확률은 길이, 높이, 두께, 대각선 길이, 무게를 사용하여 계산되어야 한다.

이러한 상황에서, 어떤 방법으로 생선의 확률을 구할 수 있을까?

2) KNeighborsClassifier를 이용한 확률 계산

가장 먼저 생각나는 방법은 바로 KNN 알고리즘을 이용하는 것이다. 즉, 어떤 Sample에 대해 최근접 이웃 10개를 찾은 후, 각 클래스의 비율을 확률 값으로 출력하는 것이다.

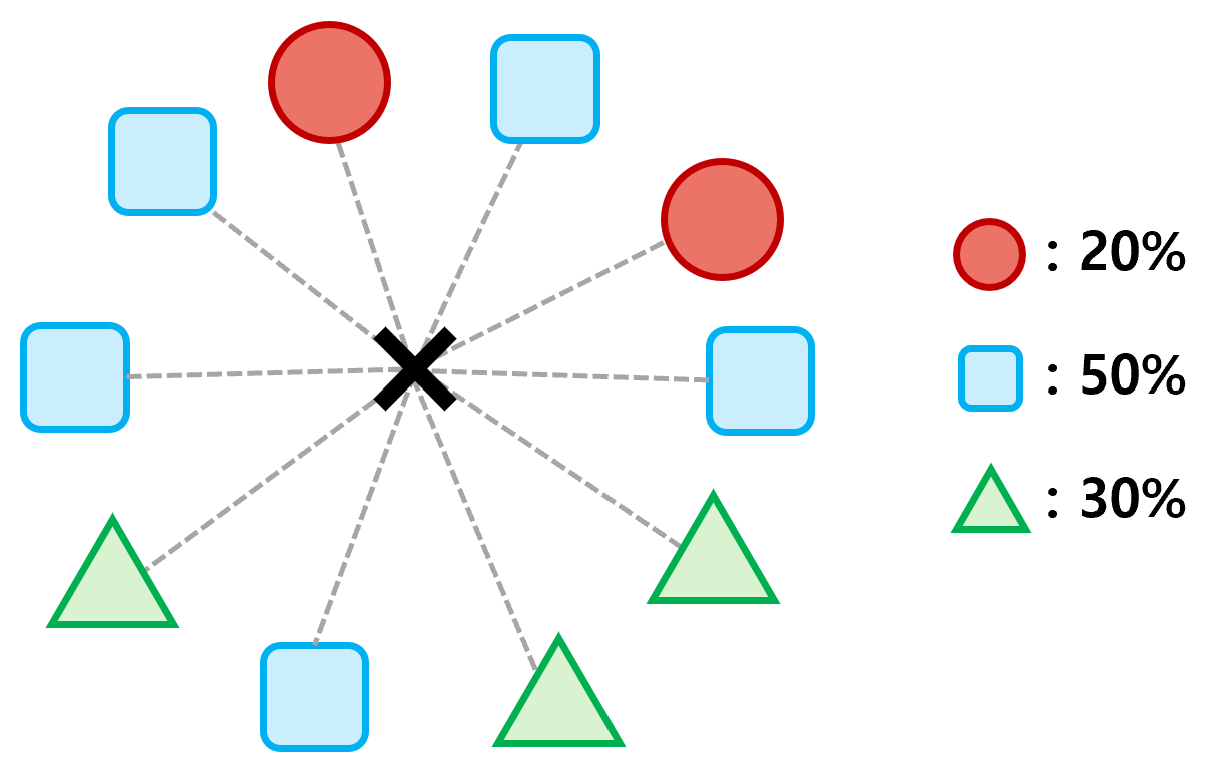
실제 KNeighborsClassifier에서도 이와 동일한 기능을 제공한다. 따라서, 이 방식으로 생선의 확률을 구해보기로 한다.

① 데이터 Set 준비를 위해 Pandas 라이브러리를 이용하기로 한다.

• head() 메서드를 통해 처음 5개 행을 테이블 형태로 출력할 수 있다.
• 참고로, CSV 파일의 첫 줄은 제목으로 자동 인식된다.

import pandas as pd

fish = pd.read_csv('https://bit.ly/fish_csv_data')
fish.head() 

② Dataframe에 어떠한 종류에 생선이 포함되어 있는지 확인해보자.

• 특정 열에 포함된 고유 값을 추출하려면, unique() 메서드를 사용하면 된다.

print(pd.unique(fish['Species']))

③ Dataframe의 Species 열은 Target 데이터로, 나머지 열(무게, 길이, 대각선 길이, 높이, 두께)은 Input 데이터로 사용하기 위해 Numpy 배열로 변환한다.

• 이 때, 입력 데이터(훈련 Set과 테스트 Set)는 2차원 배열로, 타깃 데이터는 1차원 배열로 구성해야 한다.

fish_input = fish[['Weight', 'Length', 'Diagonal', 'Height', 'Width']].to_numpy()
fish_target = fish['Species'].to_numpy()

④ 입력 데이터를 훈련 Set과 테스트 Set으로 구분하고, 변량에 대한 정규화를 수행한다.

• 정규화를 위해 StandardScaler 클래스를 사용한다.

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

train_input, test_input, train_target, test_target = train_test_split(fish_input, fish_target, random_state=42)

ss = StandardScaler()
ss.fit(train_input)
train_scaled = ss.transform(train_input)
test_scaled = ss.transform(test_input)

⑤ KNeighborsClassifier 모델을 훈련시킨다.

• k 값은 3으로 지정하기로 한다.

from sklearn.neighbors import KNeighborsClassifier

kn = KNeighborsClassifier(3) 
kn.fit(train_scaled, train_target)

⑥ 이진 분류에서 타깃을 0과 1로 구분하였듯, 다중 분류에서도 타깃을 숫자로 구분할 수 있다. 하지만, 사이킷런에서 문자열(생선 이름)을 그대로 타깃 값으로 사용할 수 있는 기능을 제공하므로, 이 기능을 사용하는 것이 더 편리할 것이다.

• 사이킷런에서 인식하는 타깃 데이터는 알파벳순으로 정렬되므로, print(pd.unique(fish['Species']))의 결과 값과 다르다는 것에 주의한다.
• 정렬된 타깃 값은 classes_ 속성에 저장되어 있다.

print(kn.classes_) 

⑦ 당연히 predict() 메서드의 반환 값도 문자열(생선 이름)로 출력된다.

print(kn.predict(test_scaled[:5]))

⑧ predict_proba() 메서드를 사용하여 각 클래스별 확률 값을 알아낼 수 있다.

• 클래스가 표기되는 순서는 kn.classes_의 순서와 같다.
• Numpy의 round() 메서드는 decimals 매개 변수에 소수점 이하 몇째 자리까지 표기할지를 전달받아 반올림을 수행한다.

import numpy as np

proba = kn.predict_proba(test_scaled[:5])
print(np.round(proba, decimals=4)) # 소수점 이하 5번째 자리에서 반올림하여 4번째 자리까지 표시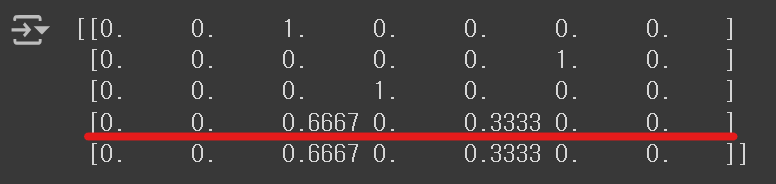

⑨ 네번째 Sample의 확률 값이 알맞게 계산된 것인지 확인해보자.

• kneighbors() 메서드에는 2차원 배열을 전달해야 한다.

distances, indexes = kn.kneighbors([test_scaled[3]])
print(train_target[indexes]) # [['Roach' 'Perch' 'Perch']] 출력

'Roach'가 다섯번째 클래스이고 'Perch' 가 세번째 클래스이니, 확률이 알맞게 계산되었다. 이로써, 생선의 확률을 구하는 데에 성공하였다. 그런데 K 값이 3이다보니, 계산될 수 있는 확률이 0, 1/3, 2/3, 1밖에 없다. 이는 K개의 이웃 중 각 클래스의 비율을 확률로 간주하다보니, 확률 모델링이 단순해지면서 발생한 문제이다.

이처럼 KNeighborsClassifier를 이용해서는 복잡한 확률 모델을 만들 수 없기 때문에, 무언가 새로운 방법을 생각해내야 할 것 같다.

2. Logistic Regression

1) 개념

바로 이러한 상황에서 사용할 수 있는 분류 모델이 Logistic Regression이다. 비록 이름에 Regression이 들어가긴 하지만, Logistic Regression은 Classification 모델이다. 그저 선형 회귀와 동일하게 선형 방정식을 학습한다는 이유로 이러한 이름이 붙은 것뿐이다. Logistic Regression 모델이 학습하게 될 방정식은 아래와 같은 형태가 될 것이다.

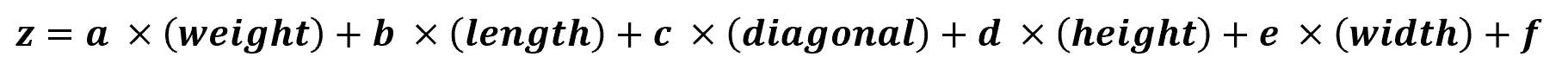
확실히 다중 회귀에서 사용하던 방정식과 동일한 형태이다. 하지만, 한 가지 문제가 있다. 위 방정식에 따라 계산되는 z의 값의 범위에 제한이 없다는 것이다. 확률은 0에서 1사이의 값이어야 하므로, z 값의 범위를 적절히 조절해주어야 할 필요가 있다.

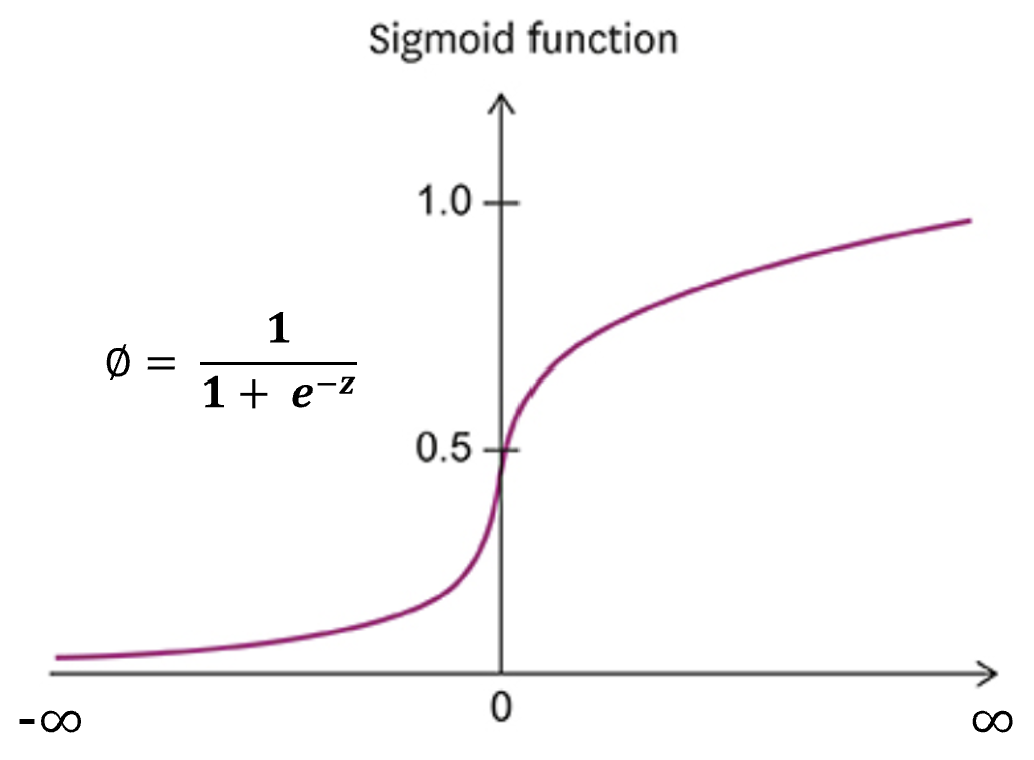
이 때 사용할 수 있는 방법이 바로 Sigmoid Function(또는 Logistic Function)이다. Simoid 함수는 아래와 같이 정의된다.

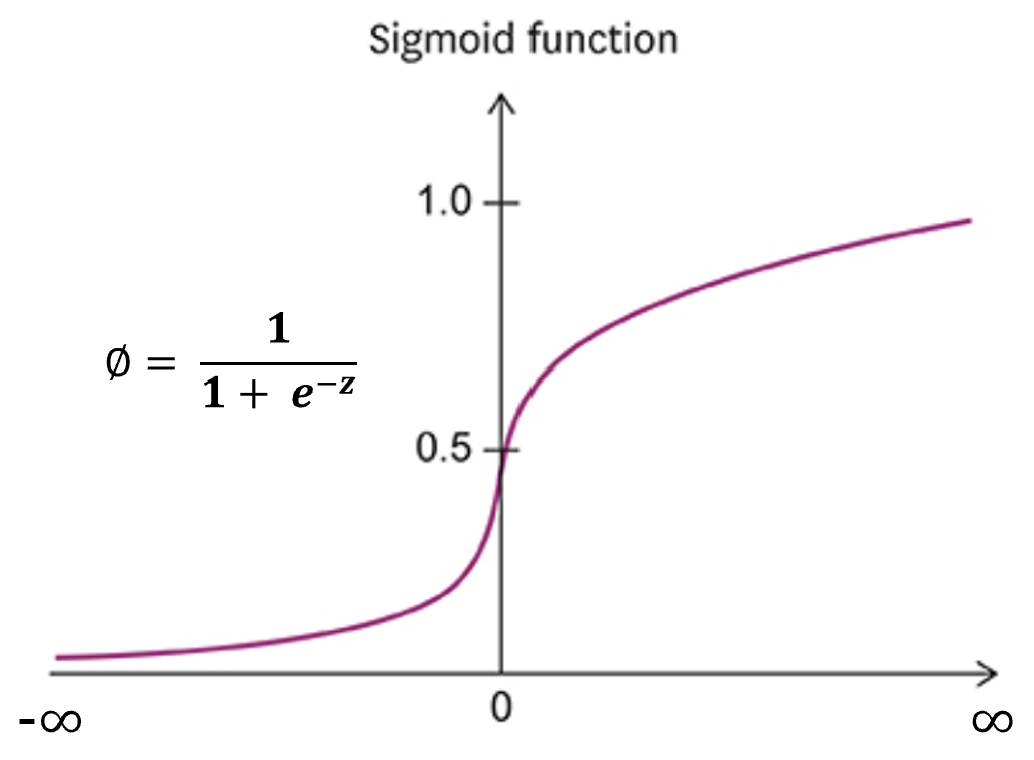
Simoid 함수는 z의 값이 음의 방향으로 커질수록 0에 가까워지고, 양의 방향으로 커질수록 1에 가까워지는 형태를 갖는다. 즉, Simoid 함수의 형태로 변환하면, z 값을 0과 1 사이의 확률 값으로 매핑할 수 있게 되는 것이다. 바로 이러한 작업을 Logistic Transformation(로지스틱 변환)이라 부른다.

2) Binary Classification

본격적인 분류 작업에 앞서 먼저는 Logistic 회귀를 이용한 이진 분류 모델을 만들어보자. 이진 분류 모델이 분류할 생선은 도미와 빙어이기 때문에, Boolean Indexing을 통해 훈련 Set에서 이 두 생선에 해당하는 Sample만 가져올 것이다. 여기서 Boolean Indexing이란, Numpy 배열의 각 원소에 True/False를 전달하여 특정 원소만 골라내는 연산을 의미한다.

Boolean Indexing을 사용하는 방법은, 배열의 인덱싱 연산자([])에 조건식을 전달하는 것이다.

characters = np.array(['A', 'B', 'C', 'D', 'E'])
print(characters[[True, False, True, False, False]]) # ['A' 'C'] 출력 

그러므로 훈련 Set에서 도미와 빙어 데이터를 골라내는 코드를, 아래와 같이 작성할 수 있을 것이다.

bream_smelt_indexes = (train_target == 'Bream') | (train_target == 'Smelt')
train_bream_smelt = train_scaled[bream_smelt_indexes]
target_bream_smelt = train_target[bream_smelt_indexes]

이진 분류를 진행하기 위한 데이터 준비가 완료되었으니, 이 데이터를 이용하여 Logistic Regression 모델을 훈련시켜보자.

from sklearn.linear_model import LogisticRegression

lr = LogisticRegression()
lr.fit(train_bream_smelt, target_bream_smelt)

다음으로 훈련된 모델을 이용해, 처음 5개 데이터의 분류 결과와 확률 값을 출력해보자.

print(lr.predict(train_bream_smelt[:5]))
print(lr.predict_proba(train_bream_smelt[:5]))

이진 분류에서는 0번 인덱스에 해당하는 클래스를 음성 클래스, 1번 인덱스에 해당하는 클래스를 양성 클래스라고 부른다. 위 모델이 도미와 빙어 중 어떤 클래스를 양성 클래스로 분류했는지 알아보려면, classes_ 속성을 확인하면 된다. (사실 알파벳 순서로 정렬되어 있기 때문에, 이진 분류에서는 굳이 확인하지 않아도 양성 클래스와 음성 클래스를 금방 파악할 수 있다.)

print(lr.classes_) # ['Bream' 'Smelt'] 출력

즉, 위의 확률 결과는 두번째 Sample을 제외한 모든 Sample이 도미일 확률이 높다고 예측했다는 의미가 되는 것이다.

※ 확률이 정확히 50 : 50이라면?
만에 하나 확률이 정확히 50:50인 경우가 발생할 경우, 사이킷런에서는 이 Sample을 음성 클래스로 예측한다. 다만, 모든 라이브러리에 공통으로 적용되는 내용은 아니며, 라이브러리에 따라 양성 클래스로 예측하는 경우도 있다.

그렇다면 이 모델이 어떠한 과정을 통해 도미와 빙어를 구분할 수 있었을까? 선형 회귀를 배울 때와 동일하게 Logistic 회귀에서 사용된 계수와 절편 값을 알아내보자.

print(lr.coef_, lr.intercept_)

즉, 모델이 학습한 선형 방정식은 아래와 같은 형태가 될 것이다.

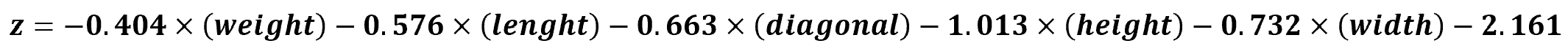
위 방정식에 따라 계산된 z 값은, decision_function() 메서드로 확인할 수 있다.

decisions = lr.decision_function(train_bream_smelt[:5])
print(decisions) 

이 z 값을 Logistic 변환하면, 확률 값을 얻을 수 있다. Logistic 변환에는 Scipy 라이브러리의 expit() 메서드가 사용된다.

from scipy.special import expit

print(expit(decisions))

이 값은 위의 lr.predict_proba(train_bream_smelt[:5])의 출력 결과에서 2번째 열과 동일하다. 이는 decision_function() 메서드가 양성 클래스에 대한 z 값을 반환하기 때문이다.

3) Multi-Class Classification

이제부터 본격적으로 Logistic 회귀를 이용한 다중 분류 모델을 만들어보기로 하겠다. 먼저 Logistic Regression을 이용한 다중 분류 모델을 훈련시키기로 하자.

lr = LogisticRegression(C=20, max_iter=1000)
lr.fit(train_scaled, train_target)
print(lr.score(train_scaled, train_target)) # 0.9327731092436975 출력
print(lr.score(test_scaled, test_target)) # 0.925 출력

LogisticRegression 클래스에 아래의 두 가지 매개변수를 전달하였다.

① C

• Logistic Regression은 Ridge 모델과 같이 계수의 제곱 값을 기준으로 규제를 적용한다.
• 하지만, Ridge와 Lasso에서 사용했던 alpha와 달리, C와 규제의 강도는 반비례한다.
• C의 기본 값은 1이므로, 규제를 완화하기 위해 20을 전달한 것이다.

② max_iter

• Logistic Regression 클래스는 반복적인 알고리즘에 기반한다.
• 최대 반복 횟수의 기본 값은 100이지만, 모델을 충분히 훈련시키기 위해 반복 횟수를 1000으로 조정하였다.

이번에도 마찬가지로 훈련된 모델을 이용해, 처음 5개 데이터의 분류 결과와 확률 값을 출력해보자.

print(lr.predict(test_scaled[:5]))
probs = lr.predict_proba(test_scaled[:5])
print(np.round(probs, decimals=3)) # 출력 간소화를 위해 반올림 수행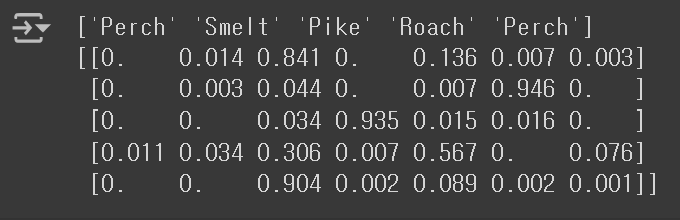

5개의 Sample에 대한 예측이므로 5개의 행이 출력되었고, 7개의 생선에 대한 확률이므로 7개의 열이 출력되었다. 이진 분류할 때보다 배열이 복잡해진만큼, 각각의 확률이 어떤 생선에 대한 확률인지 print(lr.classes_)로 확인해보는 것이 좋을 것이다.

그런데, 여기서 한 가지 의문이 생긴다. 이진 분류 모델에서는 Sample이 양성 클래스일 확률을 계산하면, 자동으로 음성 클래스일 확률을 알 수 있었다. 그런데, 다중 분류 모델에서는 특정 클래스의 확률이 다른 클래스의 확률을 결정할 수 없다. 그렇다면 이 모델은 어떻게 모든 생선의 확률을 계산할 수 있었을까? 이 의문에 대한 해답을 얻으려면, 모델이 학습한 선형 방정식의 계수와 절편을 알아보면 된다.

print(lr.coef_.shape, lr.intercept_.shape) # (7, 5) (7,) 출력

열(특성의 계수)이 5개라는 의미는, 5개의 특성이 사용되었다는 의미이다. 그런데 왜 행과 절편의 개수가 7개나 되는 것일까? 그 이유는 다중 분류의 경우, 각 클래스마다 z 값을 따로 계산하기 때문이다.

z 값은 쉽게 말해 모델이 각 클래스에 대해 갖는 확신의 정도를 수치화 한 것이므로, 각 클래스마다 z 값이 다르게 계산되는 것은 매우 당연한 일이다. 다만, 이진 분류에서 사용하던 Simoid 함수는 하나의 선형 방정식의 결과 값만 0과 1 사이의 값으로 매핑할 수 있기 때문에, 다중 분류 모델에서는 사용이 불가하다.

그래서 다중 분류에서는 여러 선형 방정식의 결과 값을 0과 1 사이의 값으로 매핑함과 동시에, 매핑된 결과의 전체 합을 1로 만들어주는 Softmax Function을 사용한다. Softmax 함수는 아래와 같이 정의된다.

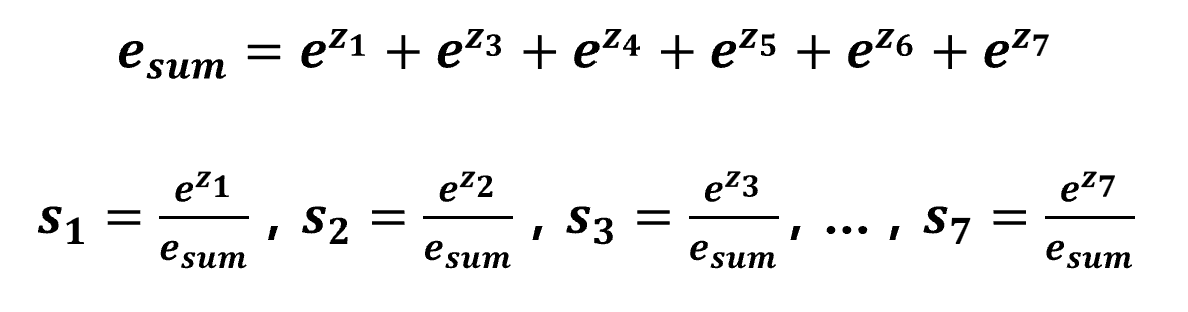
위 수식을 해석해보자.

• 지수 함수이므로, 항상 음의 값을 가질 수 없다.
• 항상 분자가 분모보다 작거나 같다.
• 따라서, 매핑 결과는 항상 0과 1 사이의 값만을 가지게 되며, 모든 매핑 결과를 더했을 때 1이 나오게 된다.

decision_function() 메서드를 이용해 7개의 z 값을 확인해보자.

decision = lr.decision_function(test_scaled[:5])
print(np.round(decision, decimals=2))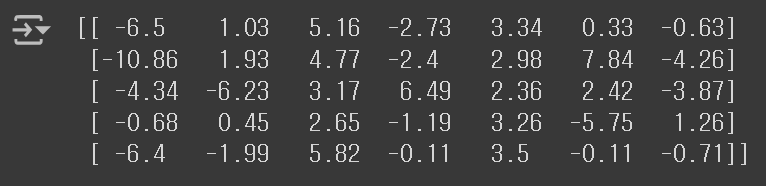

마찬가지로 z 값을 Softmax 변환하여, 확률 값을 얻을 수 있다. Softmax 변환에는 Scipy 라이브러리의 softmax 메서드가 사용된다.

from scipy.special import softmax

probs = softmax(decision, axis=1)
print(np.round(probs, decimals=3))

softmax()의 axis 매개변수는 Softmax 값을 계산할 축을 지정한다. decision 값을 보면, 각 행에 대해 Softmax 값을 계산해야 함을 알 수 있다. 각 행이라는 것은 곧 열 방향이므로 axis를 1로 지정하였다. (반대로 각 열을 선택해야 하는 경우는 행 방향이므로, axis를 0으로 지정해야 한다.)

Logistic Regression을 사용하니, KNeighborsClassifier에 비해 훨씬 더 정교한 확률 추론이 가능해졌다. 이로써, Multi-Class Classification 문제가 성공적으로 해결되었다.