
이번 포스팅에서 다뤄볼 내용은 구간 합입니다. 여기서 구간 합이란, 기존 배열을 합 배열로 바꾸어 시간 복잡도를 줄이는 알고리즘을 뜻합니다. 구간 합은 코딩 테스트에서 매우 유용하기 때문에 꼭 알아두어야 하는 중요한 내용입니다.
구간 합의 기본적인 아이디어는 i번째 원소에서 j번째 원소까지의 합을 구하기 전에 먼저 주어진 배열을 합 배열로 바꾸자는 것입니다.
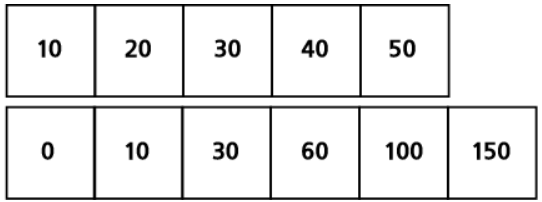
이 때, 0번 index의 원소를 0으로 설정하는 이유는 i와 j가 1부터 시작하는 숫자이기 때문입니다. 이렇게 완성된 합 배열의 j번째 원소에서 i-1번째 원소를 빼면, O(1) 시간만에 i번째부터 j번째까지의 원소의 합을 구할 수 있습니다.
1. 구간 합 구하기 1
1) Problem
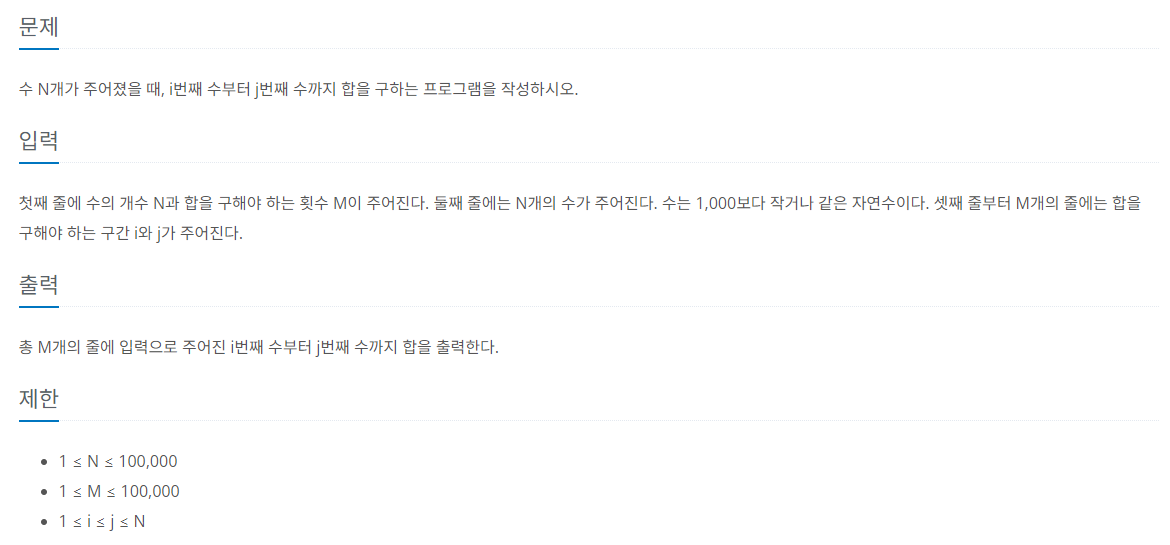
2) Test Case
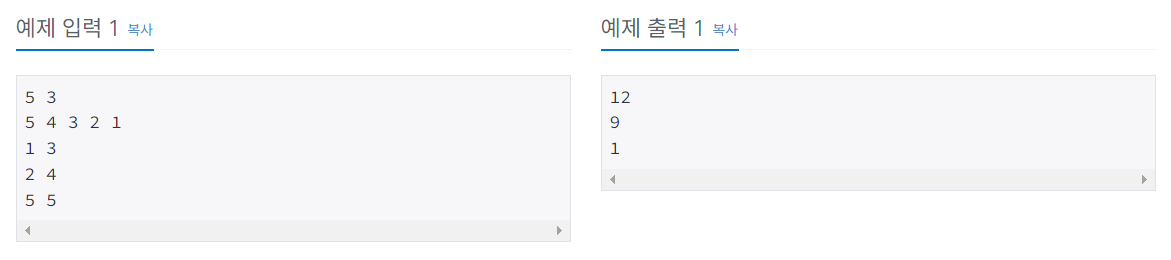
3) Solution
import sys
input = sys.stdin.readline
data_count, query_count = map(int, input().split())
num_array = list(map(int, input().split()))
sum_array = [0] # 0번 인덱스의 원소를 0으로 설정
sum = 0
for i in num_array:
sum += i
sum_array.append(sum) // append에 연산은 넣을 수 없다. 즉, append(sum += i)는 불가능하다.
for i in range(query_count):
start,end = map(int, input().split())
print(sum_array[end] - sum_array[start-1])① input = sys.stdin.readline
- input() 함수보다 빠르게 입력을 처리할 수 있어 for문 등을 이용해 대량의 입력 데이터를 입력받아야할 때 사용한다.
- 단, 개행 문자('\n')를 포함한 문자열을 반환하므로, 필요에 따라 문자열을 적절히 형변환해주어야 한다.
② data_count
- 데이터의 개수
- 리스트의 사이즈를 이용할 것이기 때문에 직접적으로 사용할 일은 없다.
③ query_count
- 질의의 개수
④ num_array
- 구간 합을 구할 대상 배열
⑤ sum_array
- 합 배열
- 반드시 0번 인덱스의 값을 0으로 설정해야 한다.
2. 구간 합 구하기 2
1) Problem
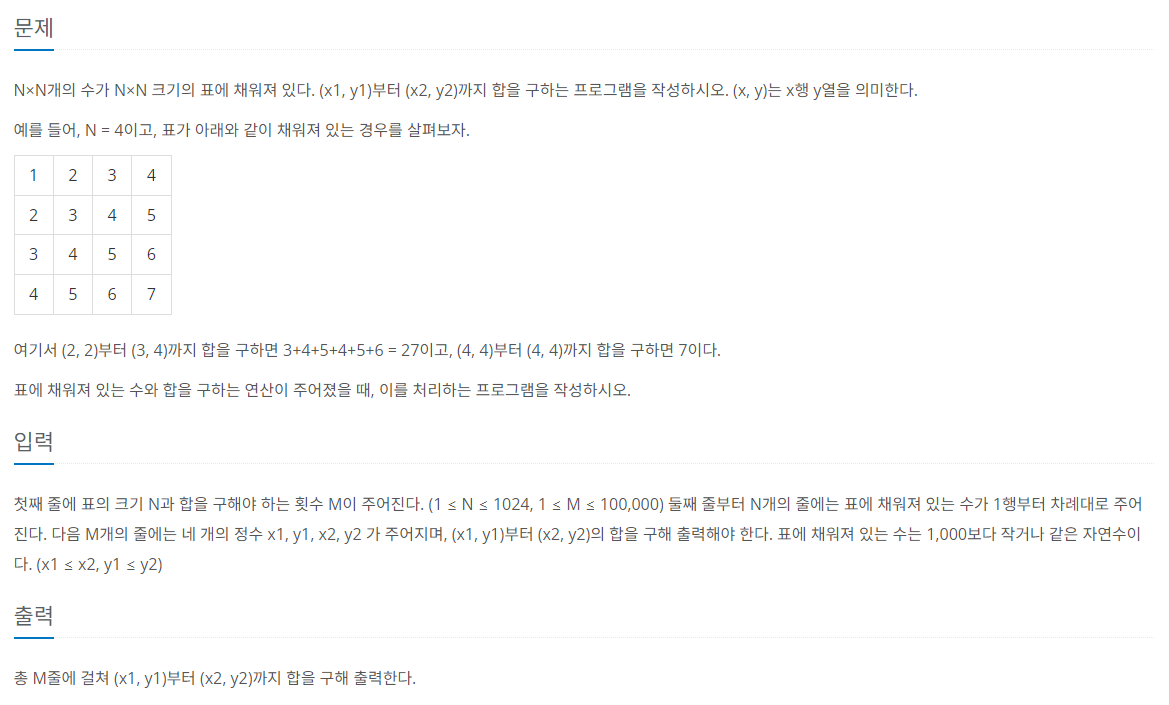
2) Test Case
3) Solution
import sys
input = sys.stdin.readline
arr_size, query_count = map(int, input().split())
arr = [[0] * (arr_size + 1)]
sum_arr = [[0] * (arr_size + 1) for _ in range(arr_size + 1)]
for i in range(arr_size):
arr_row = [0] + [int(x) for x in input().split()]
arr.append(arr_row)
for i in range(1, arr_size + 1):
for j in range(1, arr_size + 1):
sum_arr[i][j] = sum_arr[i-1][j] + sum_arr[i][j-1] - sum_arr[i-1][j-1] + arr[i][j]
for i in range(query_count):
x1, y1, x2, y2 = map(int, input().split())
result = sum_arr[x2][y2] - sum_arr[x1-1][y2] - sum_arr[x2][y1-1] + sum_arr[x1-1][y1-1]
print(result) ① arr = [[0] * (arr_size + 1)]
- arr은 문제에서 주어진 원본 배열이다.
- arr라는 2차원 배열의 첫번째 원소(2차원 배열의 원소는 1차원 배열이다)를 모든 원소가 0인 배열로 설정한다.
- 즉, arr_size가 4이면 [[0, 0, 0, 0, 0]]이 된다.
- 구간 합에서는 첫번째 행과 첫번째 열은 사용하지 않기 때문에(1부터 시작하므로) 빈 값으로 채워주고 있는 것이다.
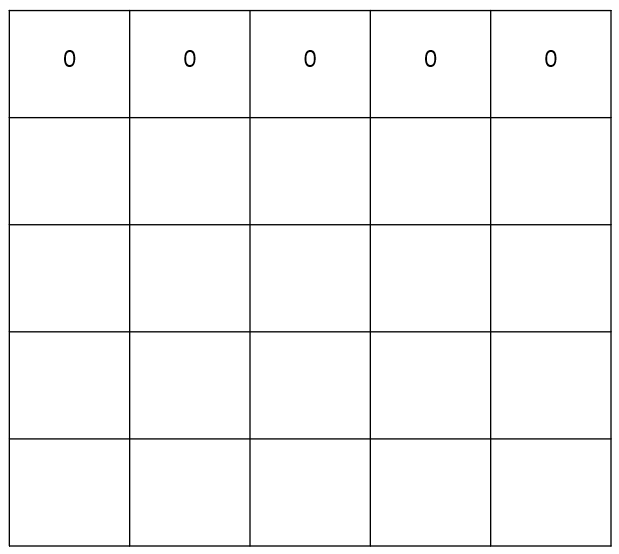
② sum_arr = [[0] * (arr_size + 1) for _ in range(arr_size + 1)]
- sum_arr은 합 배열로, (0, 0)을 기준으로 (i, j)까지의 사각형 영역 안에 있는 수의 합을 담고 있다.
- 마찬가지로, 첫번째 행과 첫번째 열은 사용하지 않기 때문에 빈 값으로 채운다.
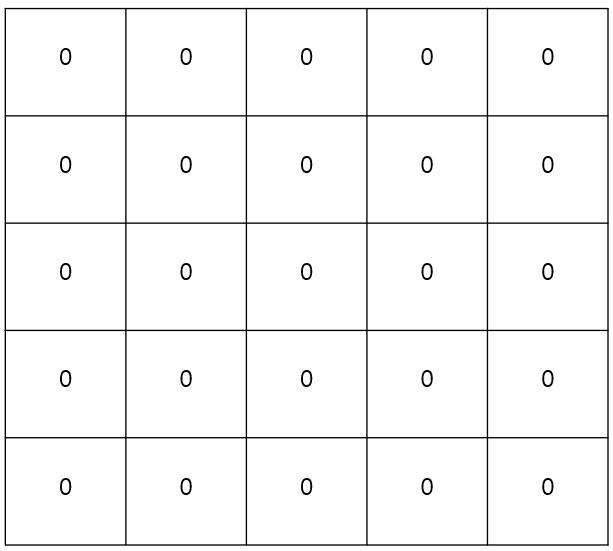
③ arr_row = [0] + [int(x) for x in input().split()]
- 입력 받은 데이터를 arr의 행으로 삽입한다.
- 첫번째 행을 사용하지 않을 것이기 때문에 0이라는 배열과 입력 값 배열을 병합해주어야 한다.
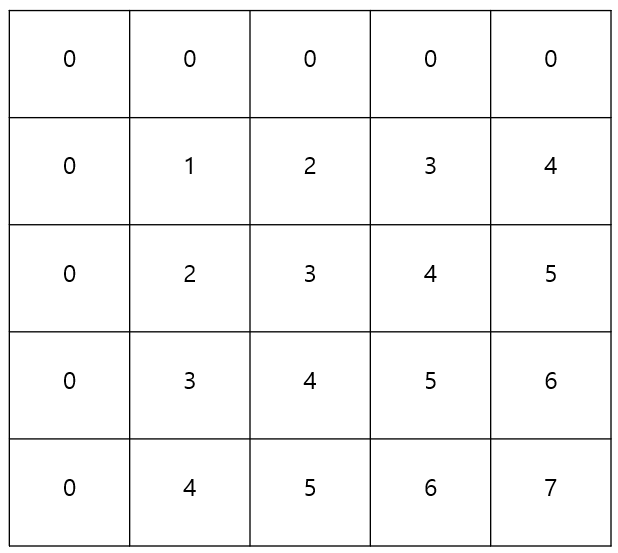
④ 이중 for문
- 배열이 1부터 시작하기 때문에, range(arr_size)를 1씩 뒤로 미룬 range(1, arr_size + 1)을 사용한다.
- 합 배열을 구하는 과정은 아래와 같다.
- 첫번째 행과 열: 기존 1차원 배열에서 합 배열을 구하는 방식과 같다.
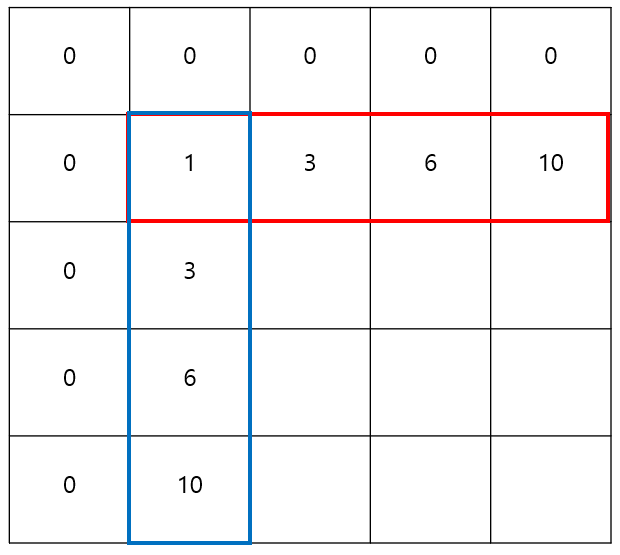
- i, j >= 2일 때의 (i, j): 주황색 부분의 값은 빨간 사각형과 파란 사각형의 값의 합에서 두번 더해진 노란 사각형을 빼고, 기존 배열의 (i, j)의 값을 더해준 것이다.
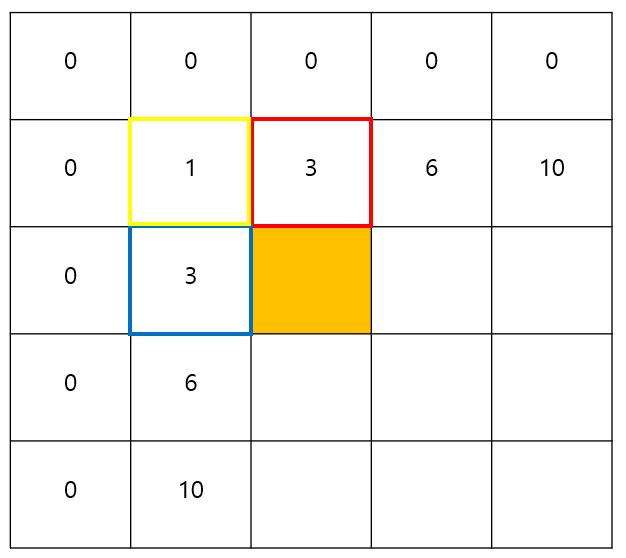
- 첫번째 행과 열: 기존 1차원 배열에서 합 배열을 구하는 방식과 같다.
- 정리하면, 0보다 큰 i, j에 대해서 다음과 같이 합 배열을 구할 수 있다.
sum_arr[i][j] = sum_arr[i-1][j] + sum_arr[i][j-1] - sum_arr[i-1][j-1] + arr[i][j]⑤ result 계산
- 기존 배열에서 (2, 2), (4, 3)이 선택되었다고 해보자.
- 노란 사각형 영역의 총 합은 (0, 0)부터 (4, 3)까지의 총 합에서 빨간 사각형의 총합과 파란사각형의 총합을 빼고, 두번 빠진 초록 사각형을 빼주어야 한다.
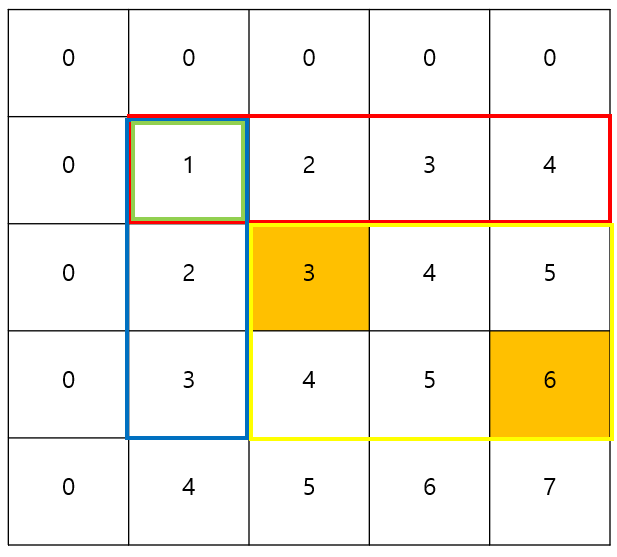
- 정리하면, 구간의 합을 다음과 같이 구할 수 있다.
sum_arr[x2][y2] - sum_arr[x1-1][y2] - sum_arr[x2][y1-1] + sum_arr[x1-1][y1-1]3. 나머지 합 구하기
1) Problem

2) Test Case

3) Solution
import sys
input = sys.stdin.readline
arr_size, division = map(int, input().split())
arr = list(map(int, input().split()))
sum_arr = [0] * arr_size # 초기화
count_arr = [0] * division # 초기화
sum_arr[0] = arr[0] # 0번째 원소까지의 합 = 0번 원소의 값
result = 0
for i in range(1, arr_size):
sum_arr[i] = sum_arr[i-1] + arr[i] # 합 배열
for i in range(arr_size):
remainder = sum_arr[i] % division
if remainder == 0:
result += 1 # 파이썬에서는 ++연산자를 지원하지 않음
count_arr[remainder] += 1
for i in range(division):
if count_arr[i] > 1:
result += (count_arr[i] * (count_arr[i]-1) // 2)
print(result)① count_arr
- 나머지를 index로 갖고, 개수를 값으로 갖는 배열
② remainder == 0인 경우
- 합 배열의 각 원소는 0번 부터 해당 index까지의 모든 원소의 합이다.
- 즉, 합 배열의 원소가 나누어 떨어진다는 것은 주어진 문제를 만족하는 경우의 수를 하나 찾은 것이나 마찬가지이다.
③ remainder != 0인 경우
- 합 배열의 나머지가 같은 경우는 서로 상쇄될 수 있음을 이용한다.
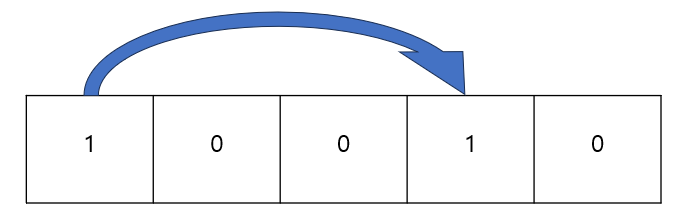
- 예를 들어 아래와 같이 합 배열을 나눈 나머지가 1로 같은 경우가 생긴다고 해보자.
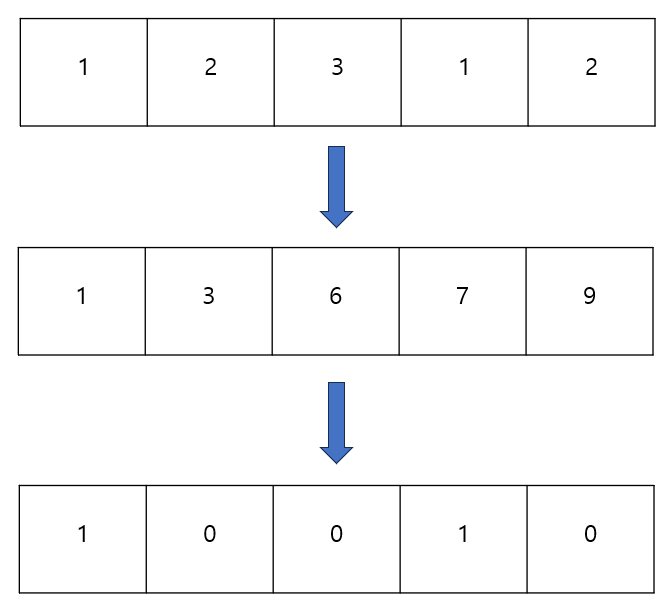
- 합 배열이기 때문에 뒤의 1은 앞의 1 때문에 생긴 것으로 볼 수 있다.
- 즉, 두번째 원소부터 4번째 원소까지의 합은 3으로 나누어 떨어지게 된다.
- 1뿐만 아니라 0에 대해서도 마찬가지이다.
④ result 계산
- 합 배열을 division으로 나누었을 때, 나머지가 0인 원소의 수만큼 증가시킨다.
- 합 배열을 division으로 나누었을 때, 나머지가 같은 수 중에서 두 개를 고르는 경우의 수(조합)만큼 증가시킨다.
