• Backprobagation
• 역전파

역전파는 딥러닝에서 핵심적인 내용이다. 수학에 익숙하지 않은 입장에서 사실 많은 수식과 미분 미분 미분을 보다보면 그냥 놓고 싶은 내용이기도 하다. 하지만 모든 곳에서 아주 중요한 개념이기 때문에 꼭 알아야할 내용으로 많은 곳에서 강조하고있다.

Backpropagation?

역전파는 인공신경망에서 모델의 예측값과 실제 결과이 차이를 후방으로 다시 보내면서 모델의 가중치를 학습시키는 것이다. 순전파에서는 입력값과 가중치를 곱하여 다음 노드로 출력하는데, 이때 사용된 가중치가 결과에 얼마나 영향을 주었는지 알아보고 학습시키는 것이 역전파라고 할 수 있다.
따라서 역전파는 미분을 통해 해당 가중치가 결과에 얼마나 영향을 주었는지 계산한다. 그리고 오차를 현재 알아보려는 가중치로 미분하는 것이 불가능하기 때문에 chain rule을 통해 원하는 결과를 얻는다.

지난 sprint challenge에서 역전파를 설명하라고 하는 것이 대한 답으로 쓴 내용이다. 이번 포스트를 통해 조금 더 자세히 정리해보겠다.

Gradient Descent

예측값과 실제값의 차이, 즉 오차를 줄이는 것이 신경망의 목표이다. 이때 오차를 줄여나가기 위한 방법이 gradient descent이다.

예를 들어 위와 같은 cost function이 있다고 하자. $x$축은 신경망의 가중치들의 벡터이고 $y$축은 cost 즉 오차이다. 우리의 최종 목표는 오차가 가장 작은 지점을 찾는 것이다. 별표시 지점이 현재 가중치 벡터의 상황이면 그때의 gradient, 미분값을 구하고 해당 값의 반대부호로 이동시켜 (가중치 값을 바꿔) 가는 것이 gradient descent이다.
이 과정을 반복하여 최종적으로 cost값이 가장 작은 점을 찾도록 한다.

Again Backpropagation

그렇다면 역전파는 어디서 쓰이는가?

gradient descent는 시각적으로 이해하면 단순히 현재의 미분값을 구하고 기울기의 반대 방향으로 learning rate만큼 씩 이동시키는 것이다. 이때, backpropagation이 이동시키는 것이라고 할 수 있다. backpropagatoin을 통해 $w$의 값을 갱신 시키고 새로운 $W$ 벡터가 나왔으므로 다시 cost function값을 구하고 gradient descent가 이루어지는 것이다.

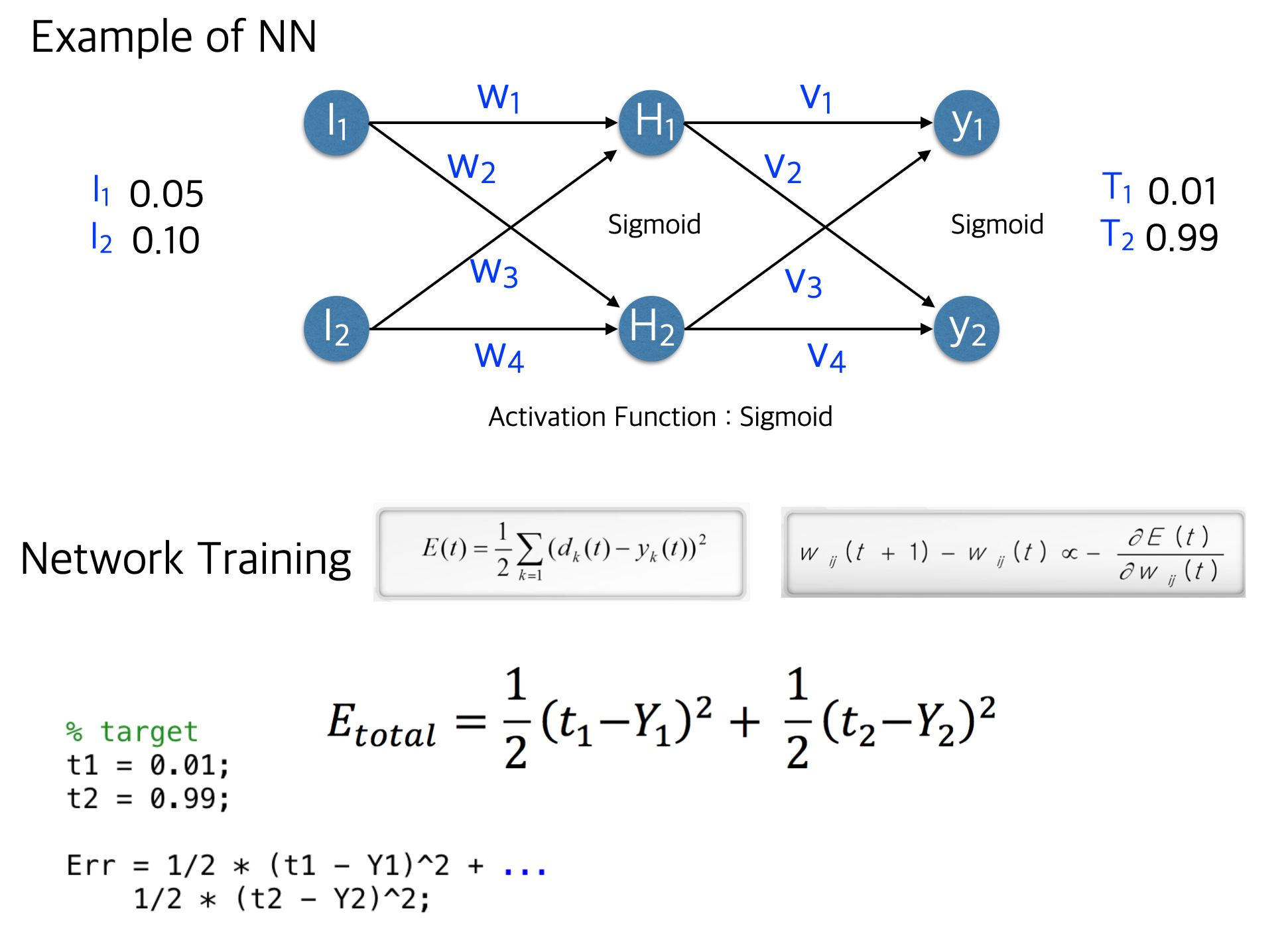
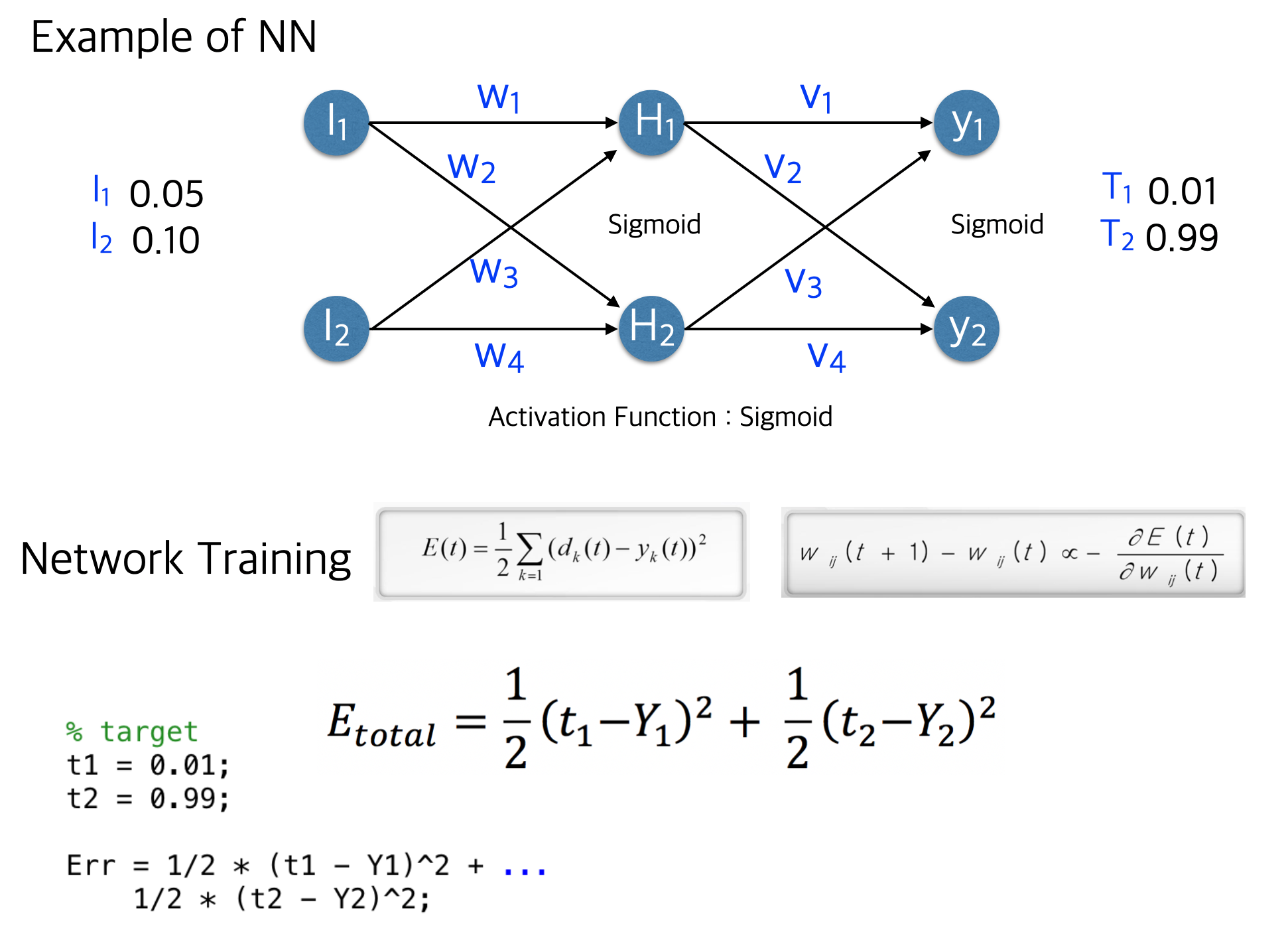
위의 예시로 다시 생각해보자. 먼저 Input data는 $I_n$ layer를 통해 입력되고 Hidden layer인 $H_n$을 거쳐 $y_n$의 출력층 결과가 나오게 된다.

그리고 cost function은 위의 그림과 같이 MSE를 예시로 들었다. 역전파는 마지막 layer부터 계산하기 때문에 $V_1$으로 cost function을 미분하면,

$Y_1$은 최종 예측값이고, $y_1$은 출력층의 결과이다. 위의 수식은 chain rule을 통해 구한 미분의 결과이고 그 결과 만큼 $V_1$을 바꾸게 된다.

python code

복잡하고 길게 설명했지만 framework를 사용한다면 코드로는 매우 간단해진다.

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
 
model = Sequential()

# 신경망 모델 구조 정의
model.add(Dense(3, input_dim=2, activation='sigmoid'))
model.add(Dense(1, activation='sigmoid'))

# 컴파일 단계, 옵티마이저와 손실함수, 측정지표를 연결해서 계산 그래프를 구성을 마무리 합니다.
model.compile(optimizer='sgd', loss='mse', metrics=['mae', 'mse'])
# model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy']) # 분류인 경우 예시

results = model.fit(X,y, epochs=50)

backpropagation은 코드로는 드러나지 않는다. 그리고 optimizer parameter를 통해 gradient descent를 발견할 수 있다.