[Programmers #12934] - 정수 제곱근 판별

(Lv. 1) 정수 제곱근 판별 (문제 링크)

문제 설명

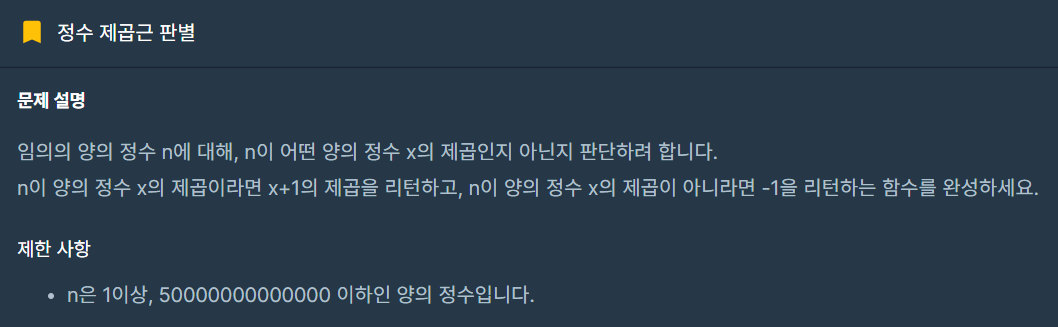
임의의 양의 정수 n에 대하여, n이 어떤 양의 정수 x의 제곱인지 아닌지 판단하려 한다.
n이 양의 정수 x의 제곱이라면 x+1의 제곱을 return하고,
n이 양의 정수 x의 제곱이 아니라면 -1을 return하는 solution 함수를 완성하라.

제한 조건

1. n은 1 이상, 50,000,000,000,000 이하인 양의 정수다.

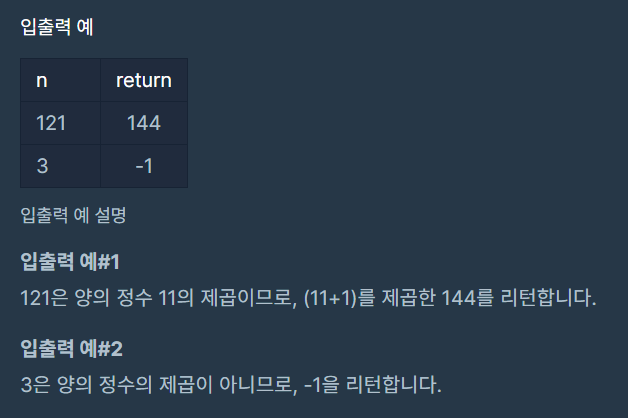
입출력 예시

---

해결 방법

1. 결과값을 출력할 변수를 선언한다.
2. Math.sqrt()를 사용하여 n의 제곱근을 구한다.
3. 정수를 구분하기 위해 Math.sqrt(n)의 값이 1로 나누어 떨어지는 지 계산한다.
   3-1. n이 어떤 양의 정수 x의 제곱수인 경우, Math.pow()를 사용하여 x+1의 제곱수를 결과값으로 설정한다.
   3-2. n이 어떤 양의 정수 x의 제곱수가 아닌 경우, -1을 결과값으로 설정한다.
4. 결과값을 출력한다.

코드

function solution(n) {
  let answer = 0;
  let sqrtN = Math.sqrt(n); // n의 제곱근

  // 정수를 구분 (소수는 1로 나눴을 때 소수 부분이 남아서 0이 아님)
  if (sqrtN % 1 === 0) {
    // n이 어떤 양의 정수의 제곱수인 경우, 해당 제곱근+1의 제곱수를 결과값으로 설정
    answer = Math.pow(sqrtN + 1, 2);
  } else {
    // n이 어떤 양의 정수의 제곱수가 아닌 경우
    answer = -1;
  }

  // 결과값 출력
  return answer;
}

---

주요 개념

• 소수는 1로 나누었을 때 나머지가 0이 아니다.
• Math.sqrt(n) : n의 제곱근을 구하는 메서드
• Math.pow(m, n) : m의 n제곱수를 구하는 메서드

개선방안

삼항 연산자를 사용하면 더욱 간단하게 표현할 수 있다.

// AS-IS
if (sqrtN % 1 === 0) answer = Math.pow(sqrt(n)+1, 2);
else answer = -1;

// TO-BE
answer = sqrtN % 1 === 0 ? Math.pow(sqrtN+1, 2) : -1;