Tree

Tree란?

앞서 다루었던 Array, Linked Listm Stack, Queue는 모두 Linear 구조를 띄고 있다.
지금부터 다룰 Tree는 이와 다르게 계층적인 구조(이름과 같이 나무처럼)를 띄는 추상모델이다.
트리는 부모-자식관계의 노드들로 구성되어 있다.
트리의 적용

먼저 트리를 배우기에 앞서 기본 용어들에 대하여 알아보자.

Root: 부모가 없는 노드. 즉, 최상위 노드. ( Depth = 0 )
Internal node: child가 적어도 하나가 있는 노드
External node(leaf): 자식이 없는 노드. 단말 노드( 맨 끝 ).
Ancestors of a node: 한 노드의 모든 상위 노드. ( itself, parent, grandparent, great-grandparent etc. )
Depth of a node: 한 노드의 조상 수(가지수)
Height of a tree: 한 트리의 노드 중 Depth의 최댓값
Descendant of a node: 한 노드의 모든 하위노드.( itself, child, grandchild etc.
Subtree : 한 노드와 그 노드의 모든 후손으로 구성된 트리
Edge(u,v): u노드와 v노드 사이를 이어주는 선. 여기서 u가 상위노드(부모)이다.
Path(v1, v2, v3,...): 엣지로 연결된 노드들로 이뤄진 시퀀스(sequence).
경로의 길이(length)는 경로에 속한 엣지의 수를 나타낸다.

---

Tree ADT

Generic methods:
size( )
empty( )

Accessor methods:
Node root( ): 루트 노드의 포지션(위치)을 리턴 - empty상태면 error를 리턴
list nodes()/positions(): 전체 노드의 포지션을 list 형식으로 리턴

Node-based methods:
Node p.parent() - 해당 노드의 부모 노드 포지션 리턴 - 해당 노드가 root라면 에러 리턴.
list p.children() - 해당 노드의 자식 노드 list 형식으로 리턴

쿼리 methods:
bool isRoot(): 해당 노드가 루트인지 아닌지 확인
bool isExternal(): 해당 노드가 단말인지 아닌지 확인

---

Tree의 순회방식

preorder Traversal(전위 순회): 루트를 먼저 방문

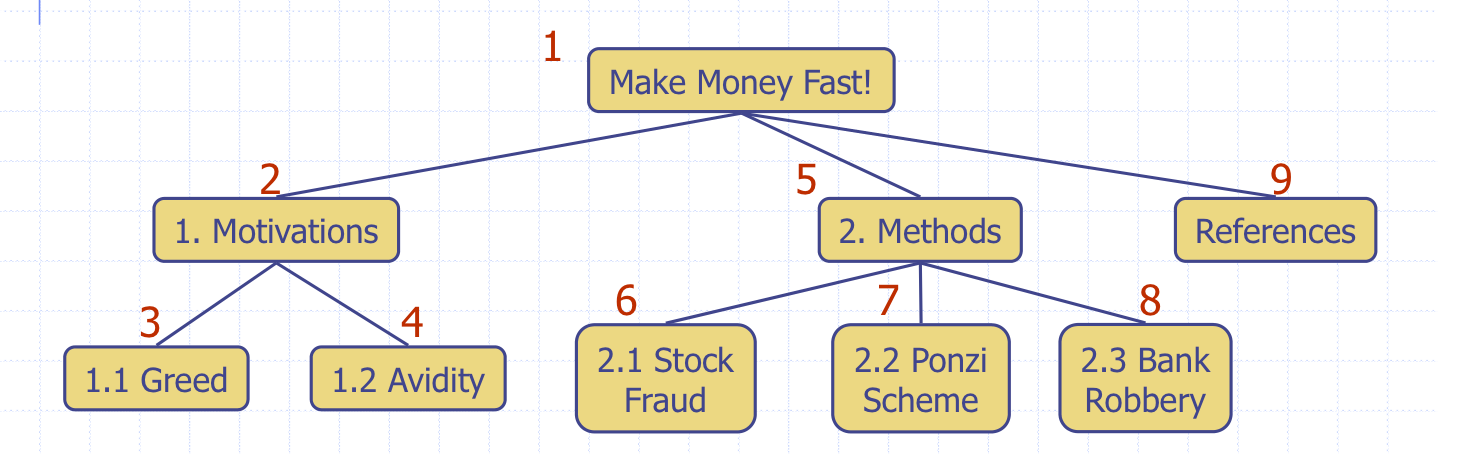
postorder Traversal(후위 순회): 루트를 마지막에 방문

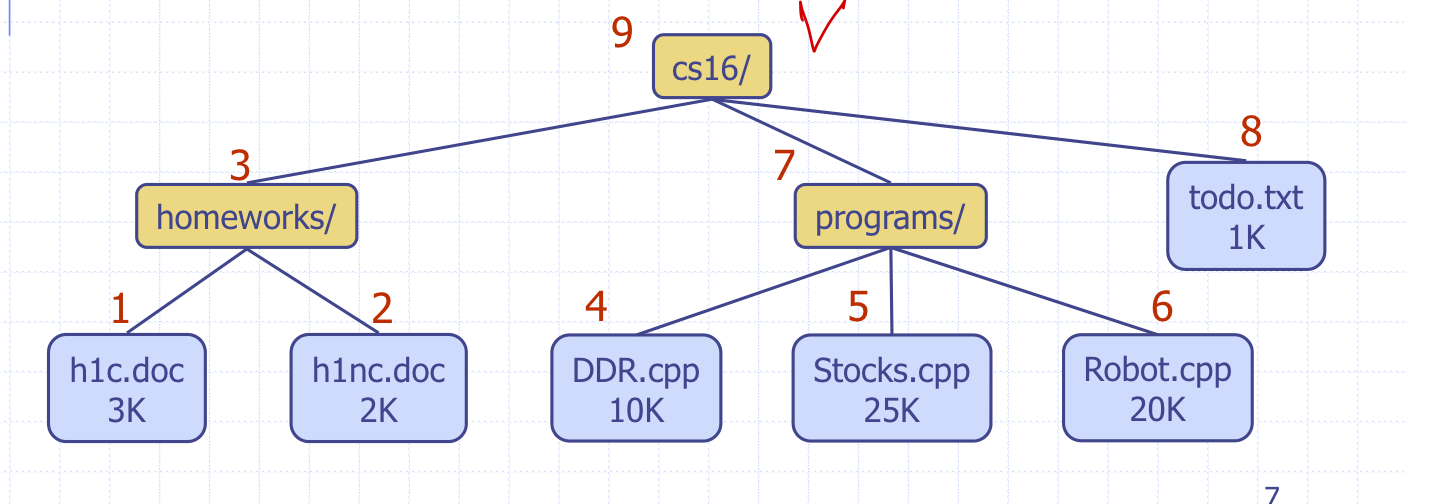
inorder Traversal(중위 순회): 왼쪽 먼저 방문

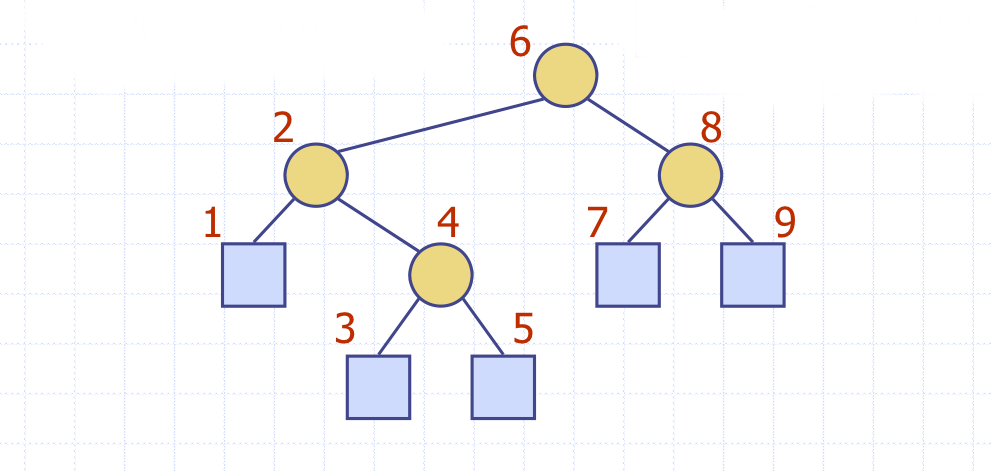
Euler Tour Traversal(오일러 투어)

• 방문하는 노드를 무조건 처리함. 한쪽 벽에 손을 대고 미로를 다니는 느낌
• prorder, inorder, postorder 방식이 섞인 순회

---

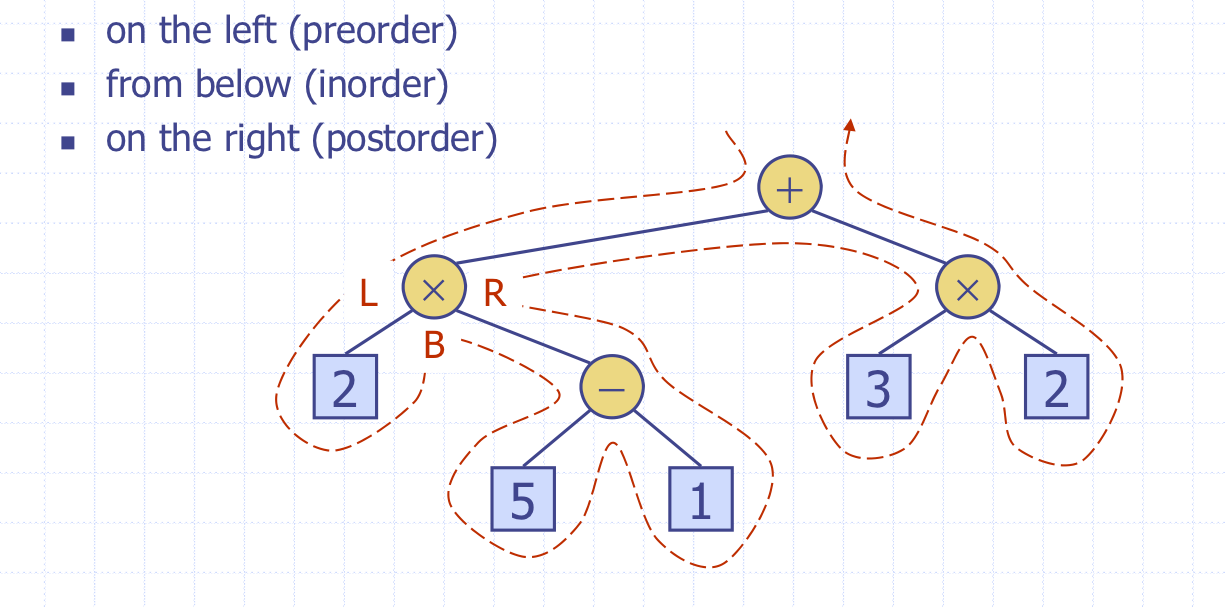
트리의 종류

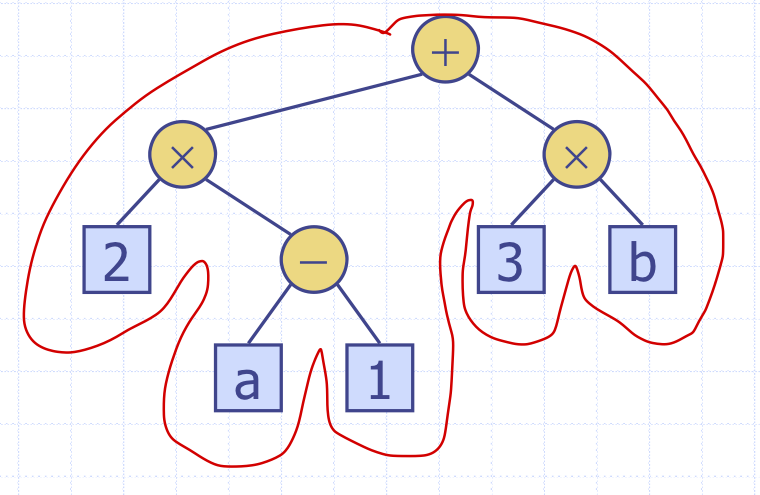
Arithmetic Expression Tree: 연산트리

• internal nodes: 연산자
• external nodes: 피연산자
  

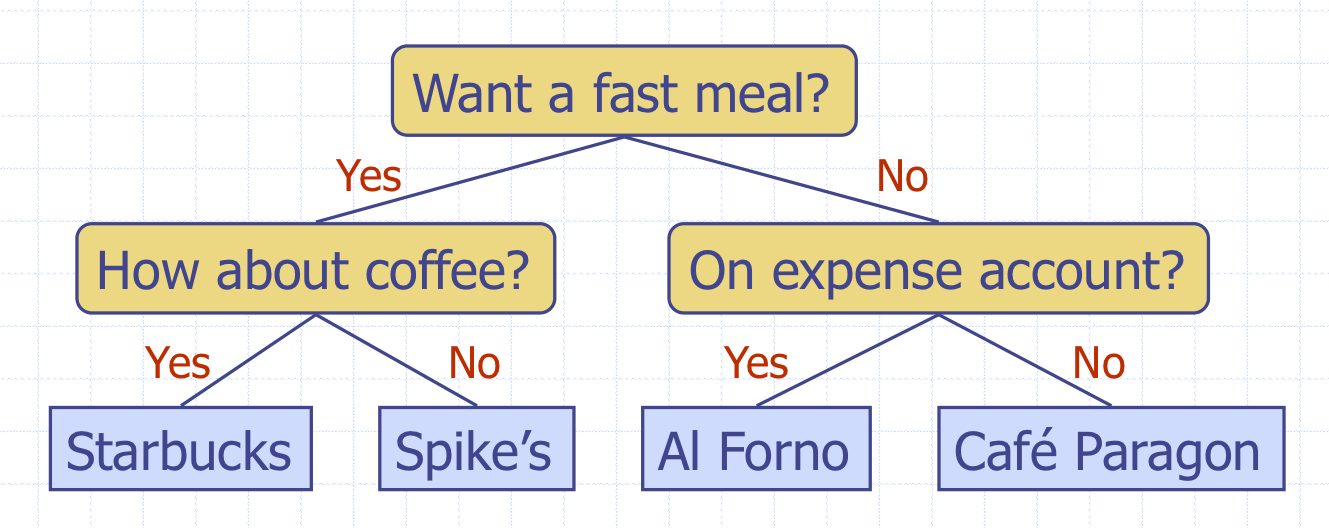
Decision Tree: 결정 트리

• internal nodes: questions with yes/no answer
• external nodes: decisions
  

Binary trees

• 각 노드는 최대 두개의 자식노드를 가질 수 있다.
• intenal 노드의 자식 노드를 각각 left child 와 right child라고 한다.

---

---Binary Tree Type---

• Full(proper) binary trees
  각 노드는 0 또는 2개의 자식을 가질 수 있음.
  

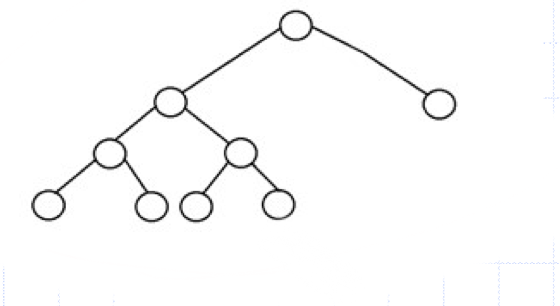
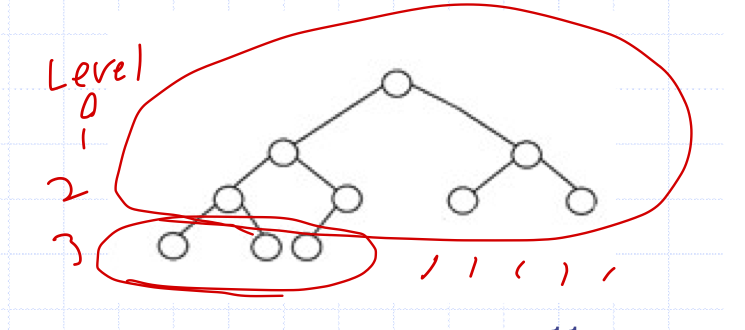
• Complete binary trees
  가장 낮은 레벨을 제외한 모든 레벨의 노드가 꽉 차있음.
  

• Perfect binary trees
  마지막 레벨까지 모두 꽉 차있음.
  

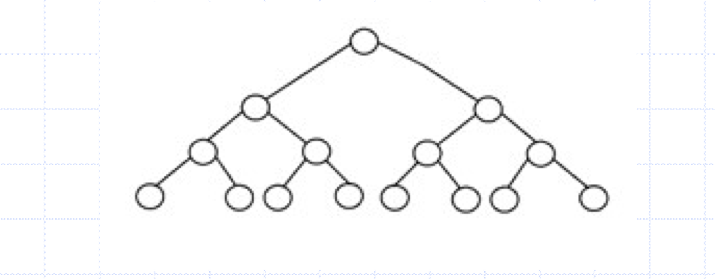
• Balanced binary trees
  왼쪽과 오른쪽 서브트리의 각 노드의 최대 차이가 1이다. (보류)

• Degenerate binary trees
  구조가 깨진 트리
  모든 인터널 노드는 하나의 자식노드만 갖는다.

  ---

Structure for Binary Tree

---

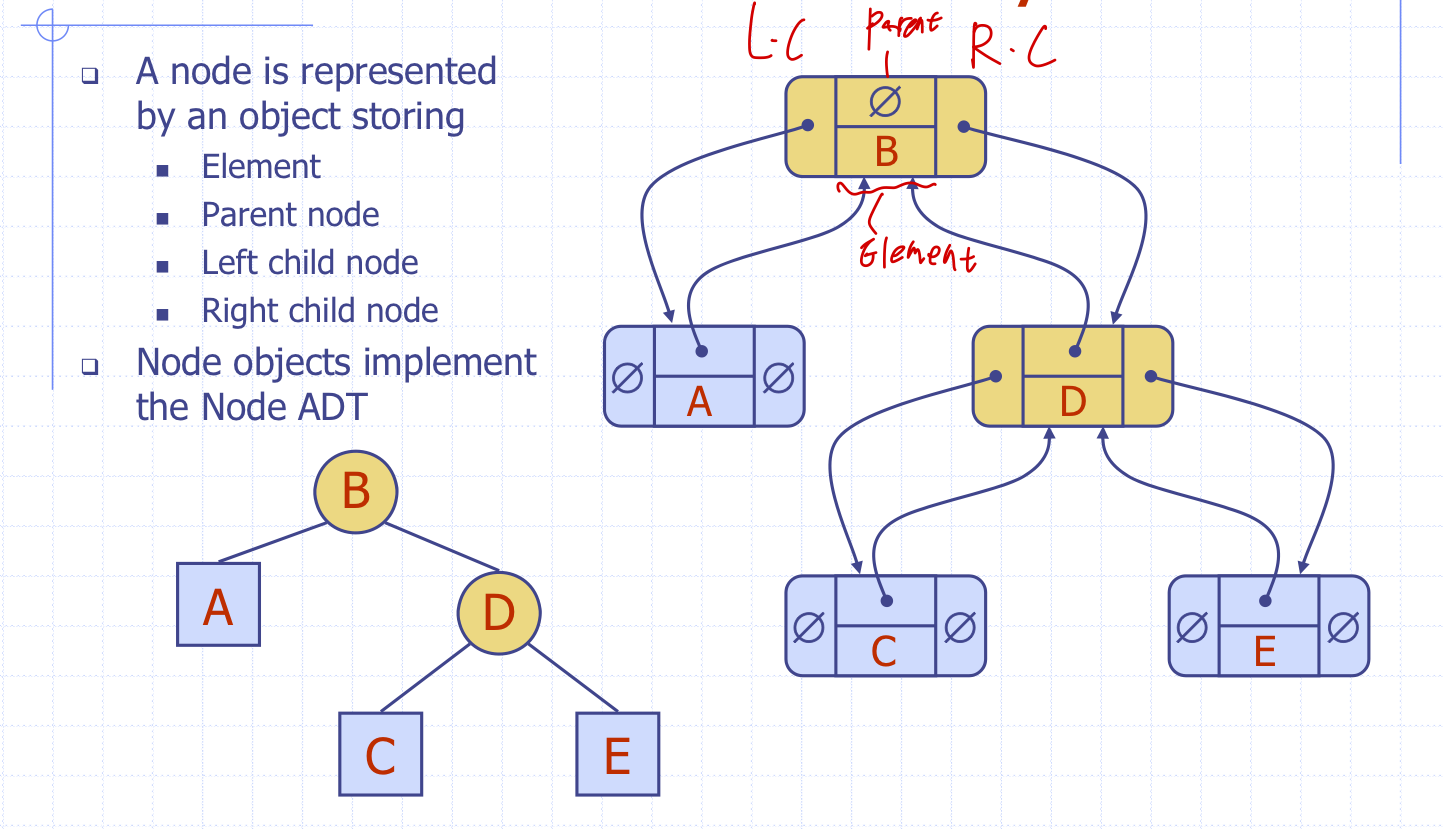
배열기반 이진트리

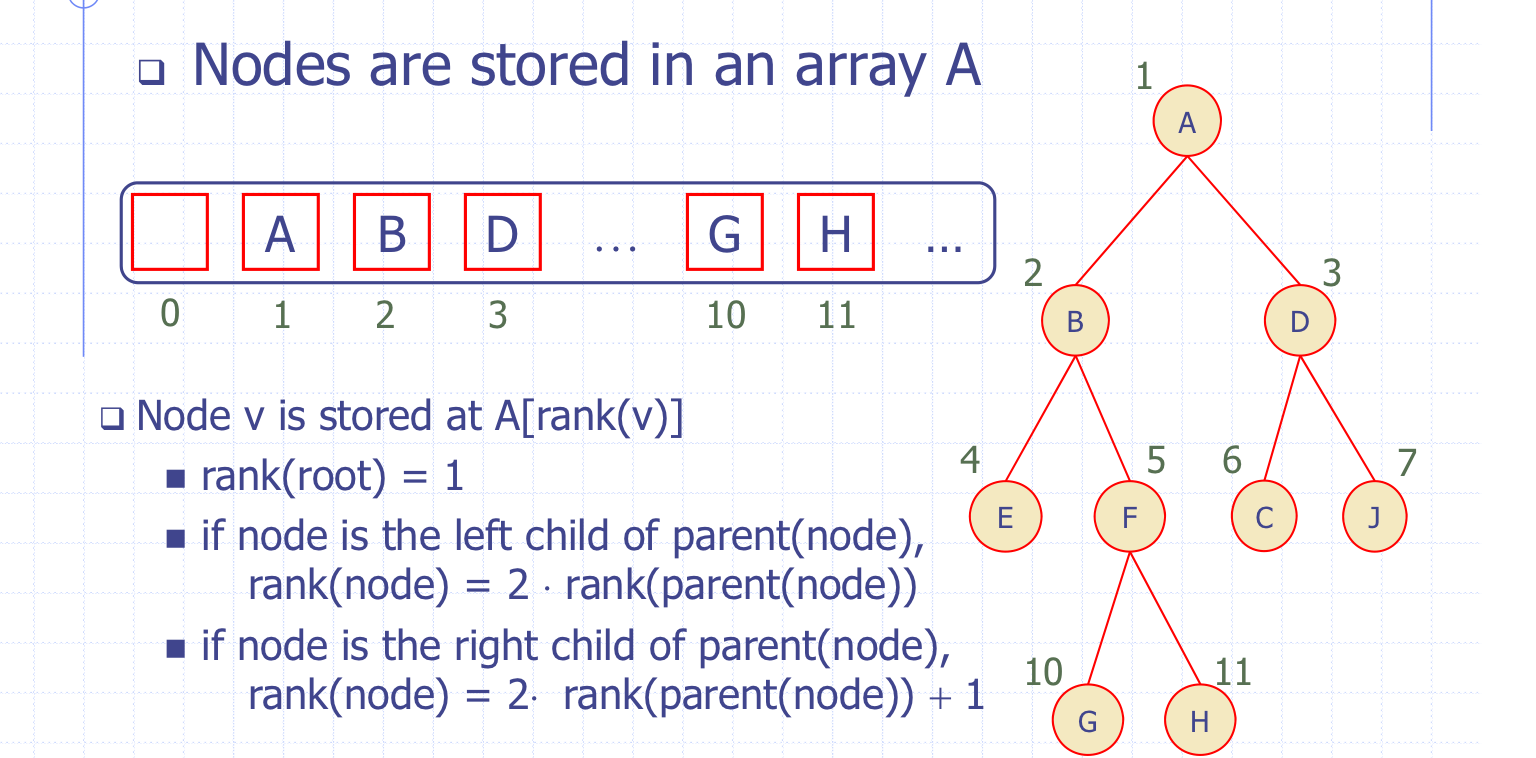
배열의 rank 규칙

• 배열 기반에서 루트노드의 랭크는 1이다.
• 이후로 같은 레벨의 왼쪽에서 오른쪽으로 랭크를 매긴다.
• 어떤 노드가 부모 노드의 left child라고 하면
  rank = 2 * rank(부모노드)
• 어떤 노드가 부모 노드의 right child라고 하면
  rank = 2 * rank(부모노드) + 1

단점: element를 저장하고 있지 않는 빈공간이 생길 수 있다.