✅문제
두 수를 입력받아 두 수의 최대공약수와 최소공배수를 반환하는 함수, solution을 완성해 보세요. 배열의 맨 앞에 최대공약수, 그다음 최소공배수를 넣어 반환하면 됩니다. 예를 들어 두 수 3, 12의 최대공약수는 3, 최소공배수는 12이므로 solution(3, 12)는 [3, 12]를 반환해야 합니다.
❕ 제한사항
- 두 수는 1이상 1000000이하의 자연수입니다.
🎹📢입출력 예제
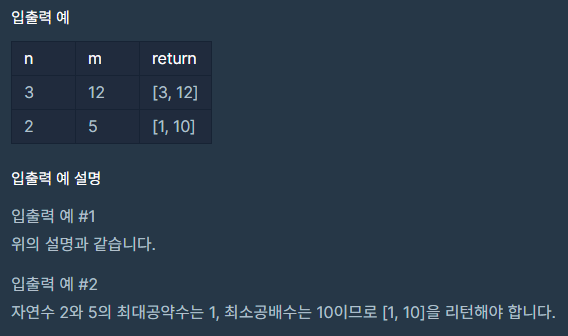
✍풀어보기
function solution(n, m) {
let answer = [];
// 유클리드 호제법을 이용해 최대공약수를 구한다.
let r, a = m, b = n;
// 큰 수에서 작은 수로 나눈 나머지 값이 0이 될 때 까지 반복한다.
while(b > 0){
r = a % b;
a = b;
b = r;
}
// 0이 되었을때 마지막으로 나눈 값 a는 최대공약수 이다.
answer.push(a);
// 최소공배수는 n과 m의 곱을 최대공약수 a로 나눈 것과 같다.
answer.push(n * m / a);
return answer;
}과거에 풀어본 적 있었는데, 까먹어서 다시 공부해서 풀었다. 일단 m이 큰 수 n이 작은 수라 가정했다. 최대공약수를 구하는 표준 방법은 소인수분해를 통해서 하는 것이지만 큰 수를 하기엔 너무 비효율적이라 유클리드 호제법 알고리즘을 통해서 효율을 올릴 수 있다.
최소공배수 * 최대공약수 = n * m이 성립된다. 그래서 최소공배수든 최대공약수든 하나만 구하면 나머지는 구하기 쉬워진다. 그래서 효율적인 측면을 따졌을 때 유클리드 호제법이 유리해서 최대공약수를 먼저 구하고 최소공배수를 구하는 것이다.
최소공배수 = n * m / 최대공약수
아래는 일반적으로 최대공약수와 최소공배수를 계산하는 방법이다.

위 예시의 최대공약수: 2 * 2 * 3 = 12
최소공배수: 2 * 2 * 3 * 3 * 5 = 180

위 예시의 최대공약수: 2 * 3 * 5 = 30
최소공배수: 2 * 3 * 5 * 2 * 3 = 180
참고 자료 및 사이트 (감사합니다)