[Java] Baekjoon 1004. 어린 왕자

문제

어린 왕자는 소혹성 B-664에서 자신이 사랑하는 한 송이 장미를 위해 살아간다. 어느 날 장미가 위험에 빠지게 된 것을 알게 된 어린 왕자는, 장미를 구하기 위해 은하수를 따라 긴 여행을 하기 시작했다. 하지만 어린 왕자의 우주선은 그렇게 좋지 않아서 행성계 간의 이동을 최대한 피해서 여행해야 한다. 아래의 그림은 어린 왕자가 펼쳐본 은하수 지도의 일부이다.

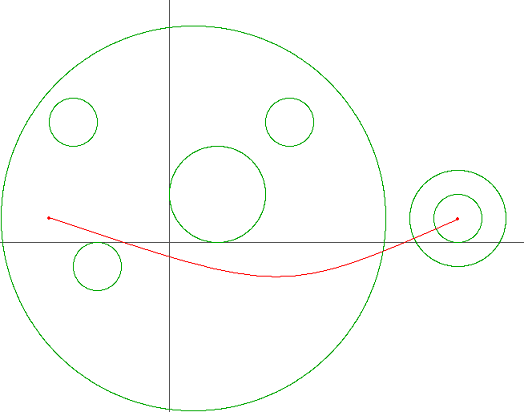
빨간 실선은 어린 왕자가 출발점에서 도착점까지 도달하는데 있어서 필요한 행성계 진입/이탈 횟수를 최소화하는 경로이며, 원은 행성계의 경계를 의미한다. 이러한 경로는 여러 개 존재할 수 있지만 적어도 3번의 행성계 진입/이탈이 필요하다는 것을 알 수 있다.

위와 같은 은하수 지도, 출발점, 도착점이 주어졌을 때 어린 왕자에게 필요한 최소의 행성계 진입/이탈 횟수를 구하는 프로그램을 작성해 보자. 행성계의 경계가 맞닿거나 서로 교차하는 경우는 없다. 또한, 출발점이나 도착점이 행성계 경계에 걸쳐진 경우 역시 입력으로 주어지지 않는다.

코드

import java.io.*;
import java.util.ArrayList;
import java.util.List;
import java.util.StringTokenizer;

public class Baekjoon1004 {
    public static void main(String[] args) throws IOException {

        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer stringTokenizer;

        Point start, destination, planet;
        List<Point> planetList;
        int T, N, answer;
        double startDistance, destinationDistance;
        boolean startFlag, destinationFlag;

        T = Integer.parseInt(br.readLine());
        for (int i = 0; i < T; i++) {
            answer = 0;
            planetList = new ArrayList<>();
            stringTokenizer = new StringTokenizer(br.readLine());
            start = new Point(Integer.parseInt(stringTokenizer.nextToken()), Integer.parseInt(stringTokenizer.nextToken()));
            destination = new Point(Integer.parseInt(stringTokenizer.nextToken()), Integer.parseInt(stringTokenizer.nextToken()));
            N = Integer.parseInt(br.readLine());
            for (int j = 0; j < N; j++) {
                stringTokenizer = new StringTokenizer(br.readLine());
                planetList.add(new Point(Integer.parseInt(stringTokenizer.nextToken()), Integer.parseInt(stringTokenizer.nextToken()), Integer.parseInt(stringTokenizer.nextToken())));
            }

            for (int j = 0; j < planetList.size(); j++) {
                planet = planetList.get(j);
                startDistance = Math.sqrt(Math.pow(planet.x - start.x, 2) + Math.pow(planet.y - start.y, 2));
                destinationDistance = Math.sqrt(Math.pow(planet.x - destination.x, 2) + Math.pow(planet.y - destination.y, 2));
                if (startDistance > planet.r) {
                    startFlag = false;
                } else {
                    startFlag = true;
                }
                if (destinationDistance > planet.r) {
                    destinationFlag = false;
                } else {
                    destinationFlag = true;
                }

                if (startFlag && destinationFlag) {
                    continue;
                }
                if (startFlag || destinationFlag) {
                    answer++;
                }
            }

            bw.write(Integer.toString(answer));
            bw.newLine();
        }

        bw.flush();
        bw.close();
    }
}

class Point {

    int x, y, r;

    Point(int x, int y) {
        this.x = x;
        this.y = y;
    }

    Point(int x, int y, int r) {
        this.x = x;
        this.y = y;
        this.r = r;
    }
}

풀이

이 문제를 쉽게 풀기 위해서는 출발점과 도착점, 그리고 입력을 통해 주어지는 행성계를 Point 클래스를 따로 만들어야 한다고 생각했다. 그래서 Point 클래스를 생성했고, 이 클래스가 가지고 있는 필드는 x(x 좌표), y(y 좌표), r(반지름)을 가지고 있다.

Point 객체들은 생성자를 통한 초기화 과정을 거치며, 출발점과 도착점은 r(반지름) 값을 지니고 있지 않기 때문에 생성자는 r(반지름) 값을 초기화 하는 생성자와 r(반지름) 값을 초기화 하지 않는 생성자, 두개로 나눴다.

출발점에서 도착점까지 도달하는데 있어서 필요한 행성계 진입/이탈 횟수를 최소화 하기 위해서는 출발점과 도착점을 포함한 행성계의 갯수를 알아야 한다. 행성계 진입/이탈은 행성계의 경계를 지나갈 때 이루어지는데, 행성계의 경계가 맞닿거나 서로 교차하는 경우는 없다고 조건을 줬기 때문에 위의 경우만 고려하면 된다.

하지만 여기서 주의해야 할 부분이 있는데, 무턱대고 출발점과 도착점을 포함한 행성계의 갯수를 바로 정답으로 출력하면 안된다. 예외인 경우가 하나 존재하는데, 그것은 바로 출발점과 도착점이 동일한 행성계의 내부에 위치 할 때이다. 이 경우는 행성계 진입/이탈이 이루어지지 않는다.

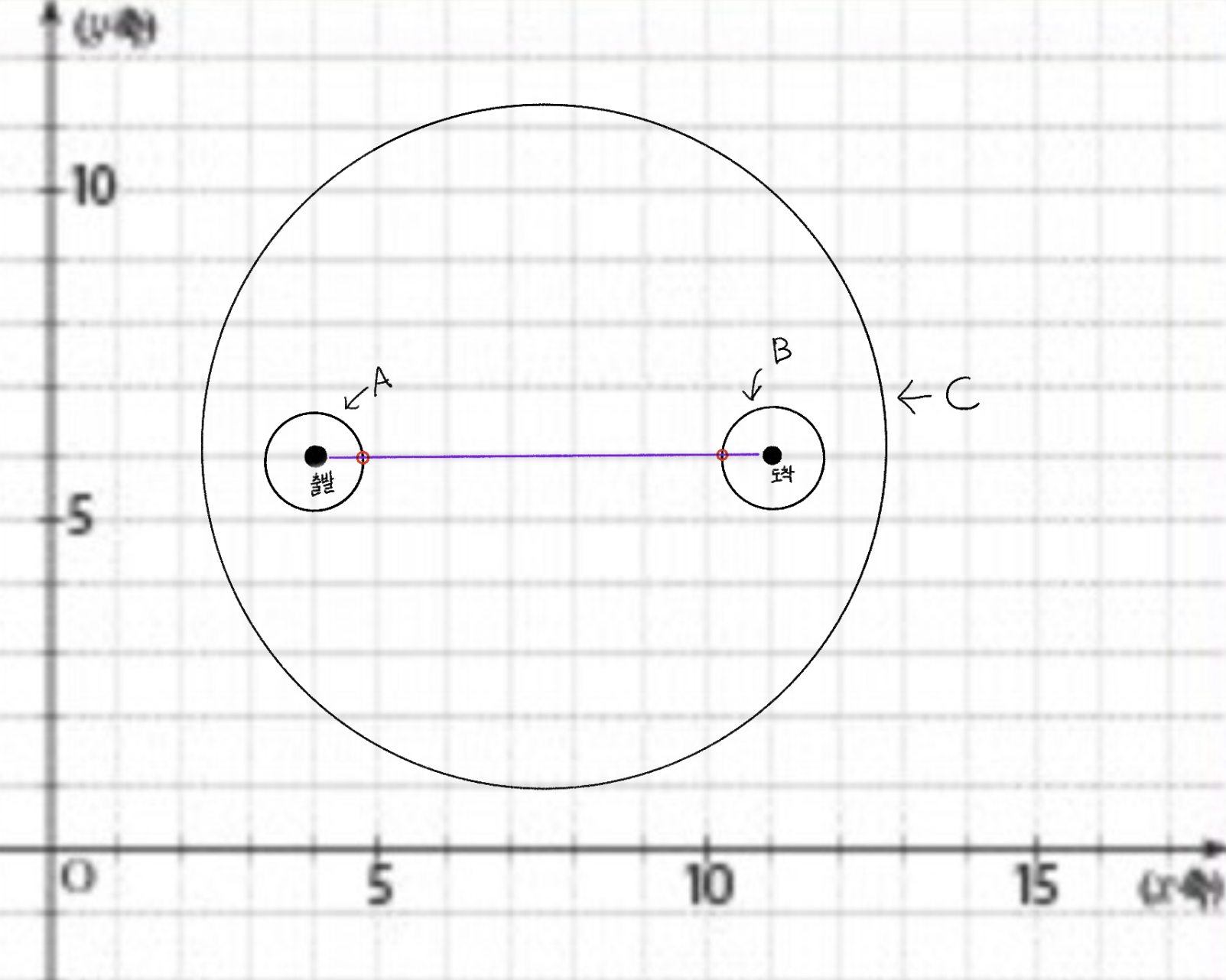
위의 그림을 보면 출발점과 도착점은 각각 A 행성계와 B 행성계 내부에 있고, 큰 C 행성계가 이를 둘러싸고 있다. 행성계 진입/이탈의 최솟값은 그림에 붉은 색 원으로 표시된 두 지점이다. 그림에 나와있다시피 출발점과 도착점을 동시에 포함한 C 행성계는 행성계 진입/이탈에 영향을 주지 않는다. 따라서 고려해야 할 부분은 출발점과 도착점 중 하나만을 포함하는 행성계의 갯수이다.

출발점(도착점)을 행성계에서 포함하고 있는지의 여부를 구하기 위해서 점과 점 사이의 거리를 구하는 공식을 사용했다. 행성계는 중심의 좌표(x, y)와 반지름(r)이 주어지기에, 만약 출발점(도착점)과 행성계의 중심 사이의 거리가 행성계의 반지름(r) 보다 작으면 출발점(도착점)은 행성계 내부에 존재하는 것이고, 크면 행성계의 외부에 존재하는 것이다.

Point 객체를 담은 List를 반복문을 돌며 객체를 받아와 출발점-중심의 거리, 도착점-중심의 거리를 구했다. 각각 startDistance와 destinationDistance에 해당한다. 그리고 둘 다 false로 초기화 된 startFlag와 destinationFlag는 각각 출발점, 도착점이 행성계 내부에 위치해 있다면 true로 값을 바꿔준다. startFlag와 destinationFlag 중 하나만 true일 경우에만 answer 값을 증가시켜주고, 두 값 모두 true일 경우에는 증가시키지 않는 식으로 정답을 도출했다.

소감

처음 문제를 읽었을 때는 어떻게 접근해야 할지 감이 잘 잡히지 않았다. 하지만 문제를 다시 자세히 읽어보고, 좌표 위에 그림을 직접 그려가면서 이해하려 해보니 길이 보였다. 앞으로 이와 같이 좌표 위에서 뭔가가 일어나는 문제들은 고민하다가 주화입마에 빠지기 전에 펜으로 그림부터 손수 그려봐야겠다!