이진트리
트리 구조는 edge와 node값으로 구성된 하나의 집합이다.
node란 해당하는 각 값을 의미하며, edge란 node와 node를 연결하는 선을 의미한다.
이진트리를 구성하는 노드는 부모 노드(parent node)와 자식 노드(child node)로 구분한다. 이 때 최상단에 위치하는 node를 root라고 부른다.
이진트리에서는 모든 노드의 자식 노드가 2개 이하인 특수한 트리 구조이다.
이진트리 구조에 대한 간략한 설명은 다음의 블로그를 참조하였다.
이진트리를 그림으로 표현하면 다음과 같이 구현할 수 있다.
그림 출처(힙 heap 자료구조 파이썬으로 알아보기)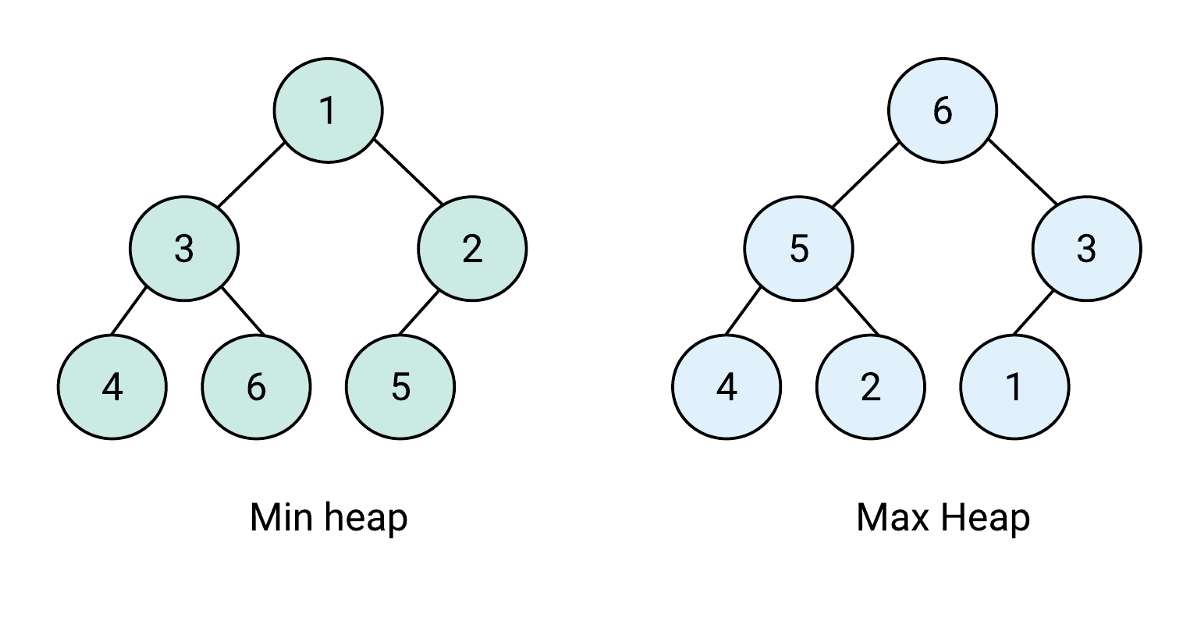
이진트리(binary tree)의 종류 중 이번 포스트에서 알아 볼 Heap 구조는 다음과 같이 두 가지로 요약할 수 있다.
왼쪽의 그림은 최소 Heap을 나타낸 것으로 트리 구조에서 부모 노드의 값이 자식 노드의 값보다 작거나 같다.
반대로 오른쪽 그림은 최대 Heap을 나타낸 것으로 부모 노드의 값이 자식 노드의 값보다 크거나 같다.
Heap 구조의 트리를 사용하는 이유는 트리 내에서 최소값과 최대값을 구하는 시간 복잡도를 줄이기 위해서이다. 일반적인 리스트 구조의 데이터에서 최소값과 최대값을 구하기 위해서는 전체 리스트를 계속하여 비교해야 하기 때문에 효율성 문제에 직면할 수 있다. 반면 Heap구조의 이진 트리에서는 전체 데이터를 구분하는 것이 아닌 부모 노드와 자식 노드를 비교하여 탐색해 나갈 수 있기 때문에 검색의 효율성이 증가한다.
heapq 모듈
파이썬 내장 모듈인 heapq 모듈은 이진트리 heap 모델 중에서도 최소 heap을 지원하는 모듈이다. 즉, 트리 내에서 가장 작은 값(최소값)을 구하기 위한 알고리즘에서 효율적으로 활용할 수 있다.
위 그림의 최소 Heap을 구하는 이진트리 그림을 보면 이해하기 쉽다. heapq 모듈에서는 최고값에 해당하는 root값이 항상 맨 앞으로 반환하며, heappop() 메서드를 통해 추출할 수 있다.
주의해야 할 점은 리스트의 두 번째 값 대소관계가 확실하지 않다는 점이다. list[0]의 값이 최소값인 것은 확실하지만, heapq 모듈은 모든 원소를 하나하나 정렬하는 sort() 메서드와는 다르기 때문에 최소값을 재추출하기 위해서는 heappop() 메서드를 다시 한 번 사용해야 한다.
위의 그림을 참고하면 쉽게 이해할 수 있다. root에 해당하는 1 원소가 최소값이라는 사실은 확인할 수 있지만, 이진 트리의 자식 노드인 3과 2의 경우 대소 관계에 따라 구분되는 것이 아님을 확인할 수 있다.
heapq 모듈이 어떠한 방식으로 원소 값을 추가하는지에 대한 공식은 다음과 같다.
[파이썬] heapq 모듈 사용법
heap[k] <= heap[2*k+1] and heap[k] <= heap[2*k+2]
위의 방식대로 이진 트리에 노드를 추가해 나가며, 이 공식에 따라 새로운 노드가 추가될 때 두 번째 값부터는 대소 관계를 명확히 알 수는 없다.
1. heappush()
파이썬에서 heapq 모듈은 내장 모듈이기 때문에 별다른 설치 과정 없이 불러오는 것으로 사용할 수 있다.
import heapq
이진 트리에 원소(노드)를 추가하는 함수는 heappush() 메서드이다.
빈 리스트를 생성하여 힙에 원소를 추가할 수 있으며 가장 작은 값이 리스트의 첫 번째 원소값으로 반환된다.
빈 리스트를 생성하여 이진 트리를 구성하는 노드를 추가해 나갈 수 있다.
tree = [] heapq.heappush(tree, 4) heapq.heappush(tree, 8) heapq.heappush(tree, 15) heapq.heappush(tree, 2) heapq.heappush(tree, 7) print(tree) >>> [2, 4, 15, 8, 7]
추가한 노드 값 중 가장 작은 값인 2 가 tree[0]에 위치한다. 출력된 tree 배열은 heap 공식에 따라 배열되었다.
2. heappop()
리스트에서 값을 추출하고 기존 리스트에서 삭제하는 pop() 메서드와 사용 방법이 같다. 다른 점이 있다면 pop() 메서드는 원소의 크기와 상관 없이 인덱스[0]에 해당하는 값을 반환하지만, heappop()의 경우 root에 해당하는 원소를 반환하기 때문에 항상 최소값을 반환한다는 점이다.
pop()을 이용해 heappop()과 같은 결과값을 얻기 위해서는 sort()메서드를 통해 리스트 값 전체를 정렬하면 가능할 것 같다. 다만 이 경우 노드의 root값을 반환하는 heappop()과는 다르게 전체 리스트를 정렬하는 것이기 때문에, 단순 추출이 아닌 반복문을 활용하는 알고리즘에서는 효율성이 떨어질 것이다.
print(heapq.heappop(tree)) print(tree) >>> 2 [4, 7, 15, 8]
최소값인 2가 반환되고 tree 리스트가 재정렬되었다.
print(heapq.heappop(tree)) print(tree) >>> 4 [7, 8, 15]
heappop() 메서드를 다시 한 번 사용하면 최소값인 4가 반환되고, 남은 원소들이 재정렬되는 것을 확인할 수 있다.
3. heapify()
새로운 노드 값을 추가하는 것이 아닌 기존의 리스트를 힙 구조로 만들 수 있다.
list = [4, 9, 32, 8, 75, 14, 2, 12] heapq.heapify(list) print(list) >>> [2, 8, 4, 9, 75, 14, 32, 12]
힙 구조로 변환되어 가장 작은 노드 값인 2가 0번째 인덱스에 온 것을 확인할 수 있다.
