최대공약수와 최소공배수

설명: 최대공약수와 최소공배수

간단 설명 : 두 수를 입력 받아 그 수의 최대공약수와 최소공배수를 구하는 간단한 문제

공약수(Common Divisor) : 두개 이상의 자연수의 공통인 약수

예)
16의 약수 : 1,2,4,8,16
20의 약수 : 1,2,4,5,10,20

공약수는 : 1,2,4

최대공약수(Greatest Common Divisor) : 공약수 중에서 가장 큰 수 이하 (GCD)

예) 위 예의 공약수는 4

공배수(Common Multiple) : 두개 이상의 자연수의 공통인 배수
최소공배수(Least Common Multiple) : 공배수 중에서 최대로 작은거 이하 (LCM)

예) 10과 12의 최소공배수
10: 10,20,30,40,50,60,70 ...
12: 12,24,36,48,60,72 ...
같은 값이 60부터 시작 한다 최소는 60인것이다. 그래서 최소공배수가 60이다.

전략 : 필자는 유클리드 호제법을 사용했다. 간단하게 예를 들어 설명하자면 12를 10으로 나누면 나머지가 2다. 그리고 또 10을 나머지인 2로 나눈다. 나누면 나머지가 안남고 딱떨어진다. 딱떨어지면 딱떨어지기전 2가 최대공약수이다. 그래서 getGCD함수에서 재귀를 써서 최대공약수를 구하였다.

또

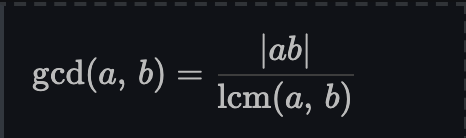
최소공배수(LCM)와 최대공약수(GCD)의 관계는 그림과 같아서 getLCM 함수에서 그대로 사용하였다.

 function getGCDLCM(n, m) {
   const getGCD = (n, m) => {
     if (m === 0) return n;
     return getGCD(m, n % m);
   };
   const getLCM = (n, m) => {
     return (n * m) / getGCD(n, m);
   };
   return [getGCD(n, m), getLCM(n, m)];
}