1-4 구간 합

코테에서 잘 나오는 내용

구간 합 : 합 배열을 이용하여 시간 복잡도를 더 줄이기 위해 사용하는 특수한 목적의 알고리즘

A 배열 {ㅇ ㅇ <ㅇ ㅇ ㅇ>} 이 구간의 합을 구하는 것

구간 합의 핵심 이론

합 배열을 구해야 함

S[i] = A[0] + A[1] + A[2] + ... + A[i-1] + A[i] // A[0]부터 A[i]까지의 합

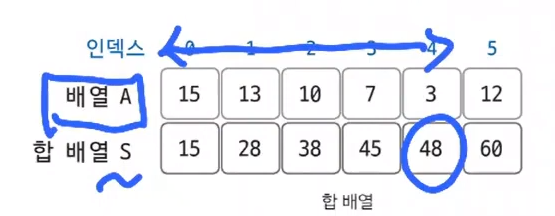
48 = 15 + 13 + 10 + 7 + 3

합 배열을 만드는 방법

합 배열 S를 만드는 공식 : S[i] = S[i-1] + A[i] //직전의 값과 원본 배열 현재 인덱스 값 더하기

A {3, 6, 5, 10, 4}

S {3, → 9 , →14, →24, →28}

구간 합 구하는 방법

구간 합을 구하는 공식 : S[j] - S[i-1]

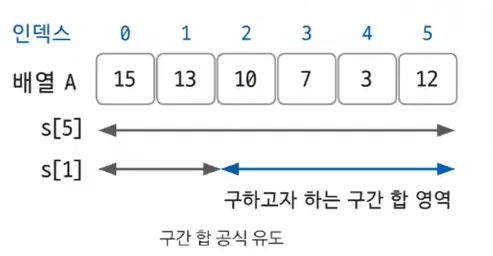
S[5] - S[1] = (A[0] ~ A[5]) - (A[0] ~ A[1]) = A[2] ~ A[5] → 구하고자 하는 부분