Problem
- Download the birthday data.
- Manually determine the pairs of you who have the same birthday. Explain your method of solution.
- Develop an algorithm for the first question using pseudo code.
- Create code that calculates the probability of having at least two students with the same birthday in a class of k students. Apply several different ks.
- Demonstrate that if there are 100 students in a classroom, it is 99.999% probable that there is a pair of students with the same birthday. Conduct computational experiments to solve this problem.
- Describe the algorithm in words as a verbal description.
- Show its correctness before you do coding. Use inductive proof.
- Show its efficiency. Use asymptotic notation and explain why.
- Construct a pseudo code for your description.
- Develop the code to solve the problem.
- Show the results.
- Apply any resources available to improve your answers and compare your original solution with others. Explain which resources you used and how you employed them.
- Please do not post the birthday data on your blog to avoid violating privacy concerns.
- If you want an argument, please refer to the following video: https://youtu.be/LZ5Wergp_PA
문제 접근
정정 기간에 이 수업을 OT 이후에 잡게 되면서 글로만 과제 내용을 파악하느라 정확히 이해한 것인지는 모르겠지만, 내가 이해한 바로는 다음 2가지를 구하는 문제라고 판단했다.
-
직접 데이터셋에서 찾아보기
주어진 데이터셋에서 생일이 같은 사람을 수동으로 결정한다.
→ 각 생일 별로 누가 생일이 같은지 비교하면서 찾아보고 어떻게 진행할지 설명한다.
-
확률을 계산해보기
k명의 학생들의 반에 적어도 두 명의 생일이 같은 학생들이 있을 확률을 계산하는 코드를 만들어라.
→ 한 교실에 100명의 학생이 있다면 생일이 같은 한 쌍의 학생이 있을 가능성이 99.999%라는 것을 증명한다.
문제 이해
생일 문제
사람이 임의로 모였을 때 그 중에 생일이 같은 두 명이 존재할 확률을 구하는 문제
23명이 모여 있으면 그 중 생일이 같은 두 명이 존재할 확률은 약 50.7%이고, 60명일 때에는 약 100%에 달한다고 한다.
1. 직접 데이터셋에서 생일이 같은 사람 수동으로 찾아보기
먼저 주어진 데이터셋을 .csv 파일로 저장하고, 이를 수작업으로 깔끔하게 가공했다. 코드를 짜서 돌려서 간편하게 진행하면 좋았겠지만 시간이 많지 않아 여기에서 시간을 많이 투자하는 것보다 과제 메인 내용에 더 시간을 많이 투자하고 싶어서 부득이하게 일일이 가공했다.
제목 행을 없애고,
김수룡,******12,03.02
김수정,******90,12.01
이름,학번,생일
이름,학번,생일
이름,학번,생일
이름,학번,생일
의 형태로 나타나게 가공했다.내가 진행한 방법은 다음과 같다.
해결 방법
-
csv파일에 들어 있는 데이터를
List<List<String>>형태로 받아온다. -
다음과 같이 같은 생일인 사람들을 담는 리스트를 만들고, 그 안에 Map형태로 key는 Double형 생일, value는 해당 생일인 사람들의 이름을 담은 집합 Set을 만든다.

-
데이터셋 앞에서부터 끝까지 돌면서, 해당 인덱스 이후에 있는 데이터 중 생일이 같은 사람이 있다면 위의 리스트에 담는다.
- 시간복잡도가 O(N^2) 으로, 완전히 탐색하는 방법이다.
-
만약 같은 생일인 사람이 있다면 해당 리스트에 들어 있는 정보들을 출력하고, 만약 같은 생일인 사람이 한 명도 없다면 없다고 출력한다.
슈도코드
CSV 파일 읽어오고 list에 담기
HashMap<Double, HashSet<String>> map (같은 생일에 어떤 사람들이 있는지) 선언
HashSet<String> set (같은 생일인 사람들의 이름 집합) 선언
ArrayList<HashMap<Double, HashSet<String>>> same_list 선언
for (i=0 ~ list크기 전까지) {
i번째 사람의 생일 추출
for (j=i+1 ~ list크기 전까지) {
j번째 사람의 생일 추출
if (i번째 사람 생일 == j번째 사람 생일) {
same_list에 넣기
}
}
}
if (같은 생일인 사람 있으면) {
for (i=0 ~ same_list 크기 전까지) {
for (same_list.get(i)의 키(생일)를 돌면서) {
해당 생일 출력
해당 생일인 사람들 이름 set 출력
}
}
} else {
생일이 같은 사람이 없다고 출력
}작성한 코드
package week1;
import java.io.*;
import java.util.*;
public class homework1 {
public static void main(String[] args) {
CSVReader csvReader = new CSVReader();
List<List<String>> list = csvReader.readCSV();
// 생일이 같은 사람을 수동으로 결정하기
boolean same_birth = false;
HashMap<Double, HashSet<String>> same_birth_and_name;
HashSet<String> same_people;
ArrayList<HashMap<Double, HashSet<String>>> same_list = new ArrayList<>();
for (int i = 0; i < list.size(); i++) {
double p1_birth = Double.parseDouble(list.get(i).get(2));
same_birth_and_name = new HashMap<>();
same_people = new HashSet<String>();
for (int j = i + 1; j < list.size(); j++) {
double p2_birth = Double.parseDouble(list.get(j).get(2));
if (p1_birth == p2_birth) {
same_birth = true;
same_people.add(list.get(i).get(0));
same_people.add(list.get(j).get(0));
same_birth_and_name.put(p1_birth, same_people);
same_list.add(same_birth_and_name);
break;
}
}
}
StringBuilder sb = new StringBuilder();
if (same_birth) {
for (int i = 0; i < same_list.size(); i++) {
for (Double birthday : same_list.get(i).keySet()) {
sb.append(birthday).append("\n");
sb.append(same_list.get(i).get(birthday)).append("\n");
}
sb.append("\n");
}
System.out.println(sb);
} else {
System.out.println("생일이 같은 사람이 없습니다.");
}
}
}
class CSVReader {
public List<List<String>> readCSV() {
List<List<String>> csvList = new ArrayList<List<String>>();
File csv = new File("D:\\Github\\Algorithm-2023-01\\practice\\src\\week1\\Algorithms - Birthday Data.csv");
BufferedReader br = null;
String line = "";
try {
br = new BufferedReader(new FileReader(csv));
while ((line = br.readLine()) != null) {
List<String> aLine = new ArrayList<>();
String[] lineArr = line.split(","); // 파일의 한 줄을 ,로 나누어 배열에 저장 후 리스트로 변환
aLine = Arrays.asList(lineArr);
csvList.add(aLine);
}
} catch (FileNotFoundException e) {
e.printStackTrace();
} catch (IOException e) {
e.printStackTrace();
} finally {
try {
if (br != null) {
br.close();
}
} catch (IOException e) {
e.printStackTrace();
}
}
return csvList;
}
}실행 결과
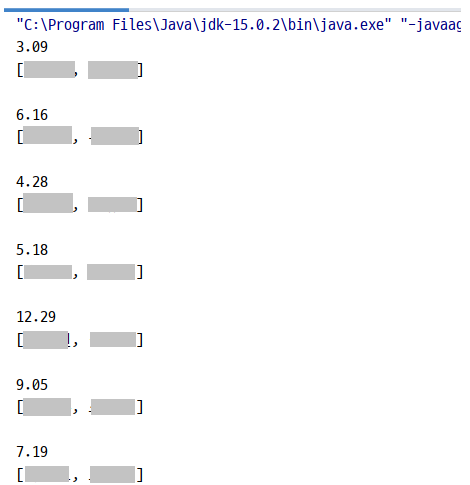
…으로 잘 나오는 것을 알 수 있다.
3.09
[이름1, 이름2]
6.16
[이름1, 이름2]
4.28
[이름1, 이름2]
5.18
[이름1, 이름2]
12.29
[이름1, 이름2]
9.05
[이름1, 이름2]
7.19
[이름1, 이름2]
1.2
[이름1, 이름2]
3.28
[이름1, 이름2]
9.25
[이름1, 이름2]
1.19
[이름1, 이름2]
2.07
[이름1, 이름2]
8.02
[이름1, 이름2]
11.15
[이름1, 이름2]
10.19
[이름1, 이름2]
Process finished with exit code 0참고 : CSV 파일 입출력 (읽기, 쓰기, 이어쓰기)
2. k명의 학생들의 반에 적어도 두 명의 생일이 같은 학생들이 있을 확률을 계산하기
가정 사항
- 2/29까지 고려하면 복잡해서 1년은 365일로 가정할 것이다.
- 365일의 가능성이 동일하다고 가정한다. → 계절적 효과가 있지만 똑같다고 가정할 것이다.
- 출생이 독립적이라고 가정한다. → 쌍둥이도 그냥 생각하지 않는다. → 한 사람의 생일이 다른 사람의 생일에 영향을 미치지 않는다고 가정한다.
a. 알고리즘 설명
k명 중 생일이 같은 두 사람이 있을 확률을 구하고자 한다.
쉬운 예시를 들자면 비 올 확률이 1/3이라면, 비가 오지 않을 확률은 1 - 1/3 = 2/3 으로 구할 수 있는데, 1에서 제외하고 싶은 경우의 확률을 빼면 우리가 원하는 확률을 구할 수 있다.
이를 적용하면, 따라서 생일이 같은 두 사람이 없을 확률을 먼저 구하고 이를 1에서 빼면 된다.
b. 귀납적 증명
예시로 23명 중 생일이 같은 두 사람이 있을 확률을 구해보자.
한 명의 생일이 1/1이라면 옆 사람이 1/1 생일이 아닐 확률은 364/365 이다.
→ 다음으로 이 두번째 사람의 생일을 1/2라고 가정하면
→ 세번째 사람은 1/1과 1/2 를 피하면 363/365이다.
그 다음 사람은 362/365…
따라서 처음 1명을 제외하고 총 22명에 대해
364/365 363/365 362/365 … 에서 항이 22개 나오면 된다.
이 식에서 규칙을 발견하면
(365-1)/365 * (365-2)/365 * (365-3)/365 … * (365-22)/365 = 약 0.5
→ 이 0.5가 23명의 생일이 모두 다를 확률이다.
1 - (생일이 모두 다를 확률) = 생일이 같은 사람이 있을 확률
→ 따라서 같은 사람이 존재할 확률 : 1- 0.5 = 0.5
이와 같은 방식으로 계산하면, 60명일 때는 약 100%에 달한다.
이 규칙을 일반화 하면
k명 중 생일이 같은 두 사람이 있을 확률을 구할 때
1 - (365-1)/365 * (365-2)/365 * (365-3)/365 … * (365-k-1)/365 의 원리를 통해 구할 수 있다.
원리 출처 : https://youtu.be/mFqZP8w0XJ0
c. 효율성
빅오 표기법으로 최악의 성능이 나올 때의 연산량을 표현하면, O(N)의 시간 복잡도가 걸린다.
n명에 대해 생일이 같은 사람의 확률을 구할 때 총 n-1 가지수를 돌면서 구하기 때문에 총 O(N) 정도의 시간 복잡도가 걸린다.
d. 슈도 코드 작성
k 입력 받음
no_match_확률 = 1로 초기화 (다음 과정에서 곱하기 때문에 1로 초기화)
for (i=1 ~ k-1까지 반복) {
no_match_확률 *= (365 - i) / 365;
}
match_확률 = 1 - no_match_확률
match_확률 출력 e. 작성한 코드
package week1;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class homework2 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int k = Integer.parseInt(br.readLine());
double no_match_prob = 1;
for (int i = 1; i <= k-1; i++) {
no_match_prob *= (double) (365 - i) / 365;
}
double match_prob = 1 - no_match_prob;
System.out.println(match_prob * 100 + "%");
}
}
f. 결과
- k = 23일 때
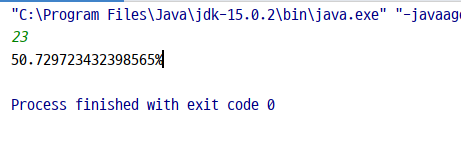
- k = 50일 때
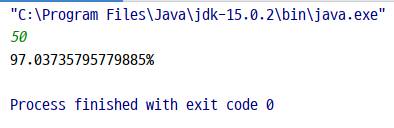
- k = 60일 때

- k = 100일 때

