1. 학습한 내용
백준 동적프로그래밍 11054번, 2565번 문제
- 11054번 가장 긴 바이토닉 부분 수열
- 2565번 전깃줄
2. 알게 된 내용
두 문제 다.. 정말 열심히 고민했지만... 너무 시간복잡도가 큰 비효율적인 풀이만 생각났고... 결국 다른 분들의 원리 설명을 읽어보면서 내가 구현해보는 식으로 공부했다.
11054번 가장 긴 바이토닉 부분 수열
설명 출처 : https://st-lab.tistory.com/136
증가하다가 어느 시점부터 감소하는지를 판단하는 게 애매했었는데,
이는 내림차순 부분수열을 거꾸로 생각해서 오른쪽에서 왼쪽으로 진행하는 거꾸로 오름차순인 부분수열로 생각하면 쉽다고 한다.
배열 앞에서부터 오름차순으로 증가 부분수열 dp를 구하고,
배열 뒤에서부터 오름차순으로 감소 부분수열 dp를 구해서
이를 인덱스를 같게 해서 합치면!
오름차순과 내림차순이 합쳐진 수열이 완성된다고 한다!
여기서 단순히 합치기만 해서는 안 되고, 원소 1개씩이 중복되어 있어서(원래 배열에서의 해당 인덱스 원소가 2번 들어감) 1을 빼주어야 한다.
이렇게 하면 바이토닉 부분 수열을 구할 수 있다.
자세히는 위의 출처 글에서 각 원소 별 수열을 참고할 것!
2565번 전깃줄
단계별로 풀어보기에서 접한 문제라서 동적프로그래밍 문제라는 것을 알긴 했지만 풀 때는 동적프로그래밍을 전혀 생각해내지 못했다... 내가 생각했던 건 가장 많이 겹치는 줄부터 하나씩 제거하면서 그 순간에 다들 몇 개가 겹치는지를 확인하려고 했다. 하지만.. 채점을 돌려봤더니 틀렸다고 떴다. 그래서 반례를 찾아보려고 질문 게시판에 들어갔는데
https://www.acmicpc.net/board/view/84972
이 글에서.. 가장 많이 꼬인 선부터 제거하는 방식으로 풀면 틀린다고 반례를 공유해주신 분의 글을 보았다.. 완전 딱 내 상황이였다... 하지만 이 반례를 보고 해결책을 생각할 때에도 동적프로그래밍을 이용하지 못했다... 너무 막혀서 결국 다른 분들의 설명을 찾아보았는데
https://yabmoons.tistory.com/572
이 글에서 정말 자세히 잘 설명해주셔서 잘 이해할 수 있었다.
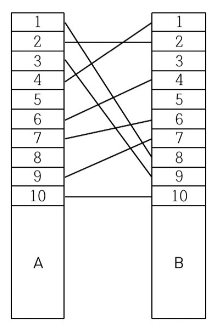
문제 속 예제 그림과 같이 A 전봇대를 기준으로 먼저 정렬을 해주고 나서 전봇대들이 꼬이지 않도록 만들어주어야 한다.
여기서 먼저 역으로 생각해서, 제거해야 하는 (1,8) (3,9) (4,1)을 먼저 제거해보겠다. 그러면 남는 것은
(2,2) (6,4) (7,6) (9,7) (10,10)
이다. 여기서 오른쪽 전봇대들의 번호를 보면, 2-4-6-7-10으로 오름차순으로 정렬되어 있다.
여기서 (없애야 하는 전깃줄의 최소 개수) = (n - 연결할 수 있는 가장 많은 전깃줄의 개수) 으로도 볼 수 있는데,
이를 이용하면 없애지 않아도 되는 전깃줄의 최대 개수는 오른쪽 전봇대에서 가장 긴 증가하는 부분수열을 구하는 과정과 동일하다.
초기의 오른쪽 전봇대 수열은 A 순서대로 정렬했으니까 A 정렬 순으로 따라가보면 [8,2,9,1,4,6,7,10]인데, 여기에서 가장 긴 수열은 [2,4,6,7,10]이다. 이러한 원리로 풀면 된다!
...
사람들은 정말 똑똑한 것 같다.. 내 머리 속에서는 정말 나오지 않는 풀이인데 진짜 대단하다.. 그리고 이 문제가 올림피아드이긴 하지만 초등부 문제였다는 게... 충격이다. 다들 정말 똑똑하신 것 같다. 나도 잘하고 싶다..! 문제 푸는데 계속 막히기만 하지만.. 다 지나고 보니 조금 재미있는 것 같..다... 동적프로그래밍 문제 혼자 뚝딱 풀고 싶은데... 쉽진 않지만... 계속 풀어서 더 잘하게 되면 좋겠다!
