(25.01.14)
문제 이해: 숫자 k개의 합이 n이 되는 경우를 모두 찾아 반환하라.
0은 고려하지 않으며, 모든 숫자는 한번씩만 사용된다. 반환 리스트 순서는 상관없다.
문제 접근
이전에 백트레킹 이용해 조합 개수 추출하는 함수를 공부했던 적이 있었다.
(25.01.20)
조합을 추출할 수 있다면, 1~n까지의 수의 경우를 추출한 뒤 합이 n이 되는 경우만 반환시키면 문제 해결이 가능하다.
이전에도 백트래킹을 이용한 조합 개수 추출이 이해가 잘 안됐었는데, 아직도 잘 모르겠으니 다시 한번 공부한다고 생각하거나 아예 알고리즘을 외워보자.
class Solution {
public List<List<Integer>> combinationSum3(int k, int n) {
List<List<Integer>> result=new ArrayList<>();
findCombinations(k, n, 1, new ArrayList<>(), result);
return result;
}
private void findCombinations(int k, int target, int start, ArrayList<Integer> current, List<List<Integer>> result) {
if(k==0 && target == 0){
result.add(new ArrayList<>(current));
return;
}
if(k==0 || target<0){
return;
}
for(int i=start; i<=9; i++){
current.add(i);
findCombinations(k-1, target-i, i+1, current, result);
current.remove(current.size()-1);
}
}
}(25.01.22)
우선 구현해야하는 함수를 다시 정리해보자. 그리고 최대한 내가 생각해보기도 하자.
- Combination Sum III은 입력으로 숫자의 개수인 k, 합이 되어야하는 수인 n을 받아서 서로 다른 수로 합이 n이 되는 경우들을 List<List>로 반환하면 된다.
가장 쉽게 접근 가능한 방법은 for문을 이용해 구현하는 것이지만, 가능한 숫자들을 for의 변수로 사용하게되면 코드를 k번의 for루프가 필요하기에 코드상으로 구현하는 데에 한계가 있다는 문제가 있다.
어떻게하면 k개 서로다른 수의 합이 n이되는 경우를 찾아낼 수 있을까?
문제 접근 1
모든 숫자를 나타내기 위해 아래와 같은 방법을 생각해볼 수 있다.
문제의 조건에서 모든 수는 0~9의 값이어야 하는데, 위와 같은 접근에서는 특정 수가 10이상일 경우를 필터링하기 어렵기 때문에 다른 방법이 필요해보인다.
문제 접근 2
아예 0~9의 꼴을 가진 k개의 숫자를 전부 확인하며, 합이 n이 되는 경우를 따로 리스트에 추가하면 어떨까? 경우의 수는 9^k가 된다.
예를 들면 k=5일 때 아래와 같이 경우를 순회해야한다.
01234
01235
...
01239
...
56789
위처럼 하나의 숫자로 취급하여 다루게 되면 그냥 수를 +1씩 더하면 된다!
시작되는 수는 0~(k-1)까지의 합이기에 k(k-1)/2로 찾을 수 있다.
끝나는 수는 (10-k)~9까지의 합이기에 9(9+1)/2-(9-k)x(10-k)/2로 찾을 수 있다.
코드 구현 다 했는데 문제를 다시 읽어보니 0은 포함시키지 않는다. 그럼 시작 숫자를 12345가 되도록 k(k+1)/2로 바꾸자.
그리고 위 방법은 수가 중복될 수 있다는 치명적인 단점이 있다.. 그리고 시작 수를 조절한다고 해도 0이 포함된다..
class Solution {
private int sum_of_digits(int num){
int result=0;
int i=num;
while(i/10!=0){
result+=i%10;
i/=10;
}
result+=i%10;
return result;
}
private List<Integer> intarr_to_IntegerList(int num){
List<Integer> result=new ArrayList<>();
while(num/10!=0){
result.add(num%10);
num/=10;
}
result.add(num%10);
return result;
}
public List<List<Integer>> combinationSum3(int k, int n) {// 숫자 k의 합이 n이 되어야 한다.
List<List<Integer>> result=new ArrayList<>();
int start_num=0;
for(int i=1; i<=k; i++){
start_num*=10;
start_num+=i;
}
int end_num=0;
for(int i=10-k; i<=9; i++){
end_num*=10;
end_num+=i;
}
for(int num=start_num; num<=end_num; num++){
int sum=sum_of_digits(num);
if(sum==n){
System.out.println(num);
result.add(intarr_to_IntegerList(num));
}
}
return result;
}
}최대한 위 코드를 살려보기 위해 0이 포함되면 넘어가게 하거나 set을 이용하여 순서를 없애는 둥의 시도를 해볼 계획이다.
(25.01.23)
기존에 생각해낸 1234꼴의 정수로 문제를 풀이하는 것은 굉장히 좋은 접근이라고 생각한다.
그 이유는 불필요한 숫자까지도 확인해야한다는 것이 비효율 적이지만 전반적인 순회 자체의 속도와 연산이 정수연산 +1이기 때문이다.
중복되는 수의 사용과 0의 사용을 체크하기 위해 is_valid함수를 구현해보자. 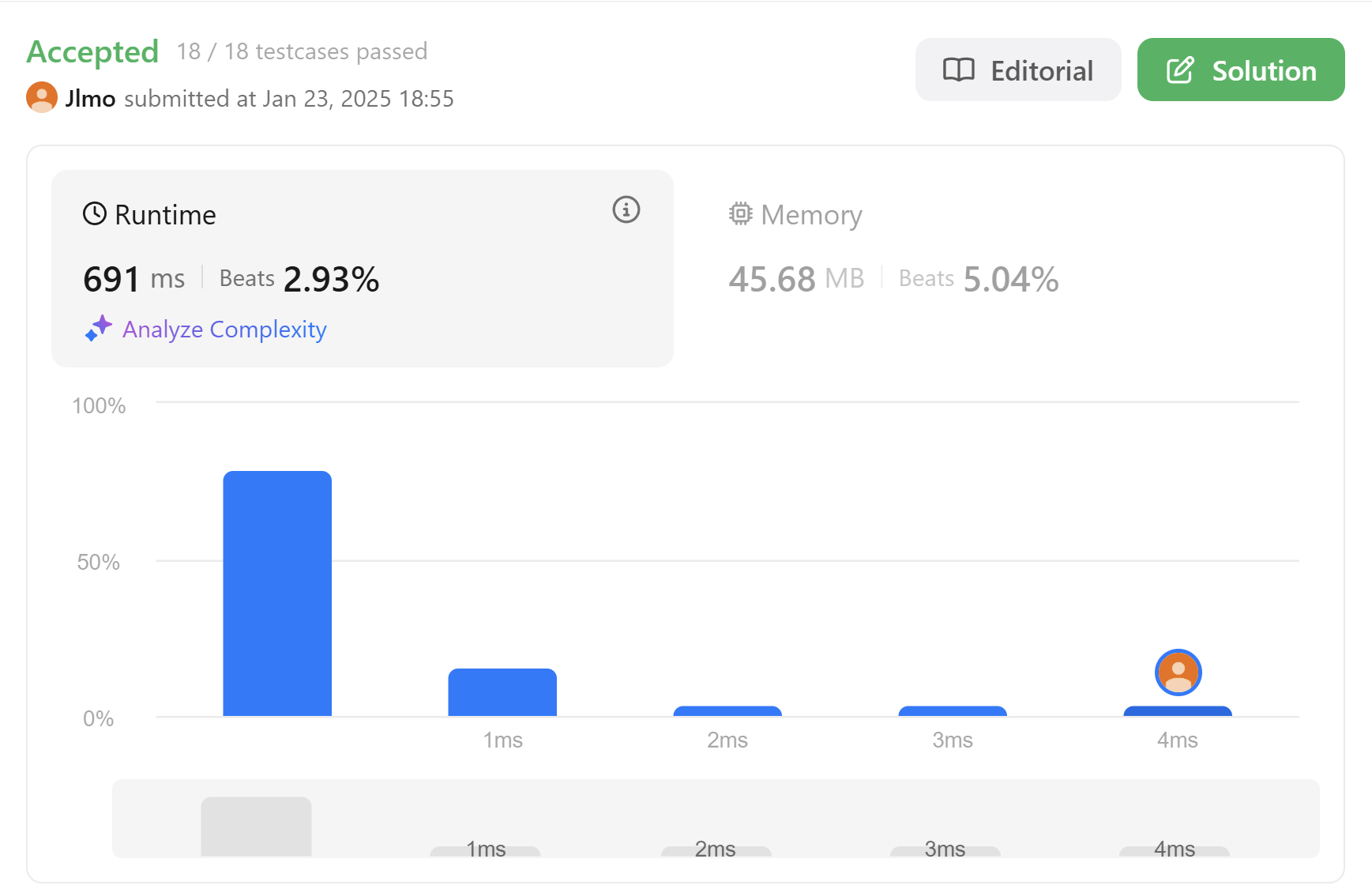
와 백트레킹 없이 내 알고리즘으로 문제를 해결하였다!!! 불필요한 수를 확인하지만 확인 속도가 빠르기에 문제 없을 것이라는 내 예상이 맞았다.
아래는 현재의 코드인데, 최적화를 시도해보자.
class Solution {
private int sum_of_digits(int num){
int result=0;
int i=num;
while(i/10!=0){
result+=i%10;
i/=10;
}
result+=i%10;
return result;
}
private List<Integer> intarr_to_IntegerList(int num){
List<Integer> result=new ArrayList<>();
while(num/10!=0){
result.add(num%10);
num/=10;
}
result.add(num%10);
Collections.sort(result);//중복 확인을 위해 내부 순서 정렬하여 저장
return result;
}
private boolean is_valid(int num){
List<Integer> numarr=intarr_to_IntegerList(num);
//중복되는 수가 있는지 체크
int distinct_size=numarr.stream().distinct().collect(Collectors.toList()).size();
int origin_size=numarr.size();
if(distinct_size!=origin_size){
return false;
}
//0이 있는지 체크
if(numarr.contains(0)){
return false;
}
return true;
}
public List<List<Integer>> combinationSum3(int k, int n) {// 숫자 k의 합이 n이 되어야 한다.
List<List<Integer>> result=new ArrayList<>();
int start_num=0;
for(int i=1; i<=k; i++){
start_num*=10;
start_num+=i;
}
int end_num=0;
for(int i=10-k; i<=9; i++){
end_num*=10;
end_num+=i;
}
for(int num=start_num; num<=end_num; num++){
int sum=sum_of_digits(num);
if(sum==n && is_valid(num)){
System.out.println(num);
result.add(intarr_to_IntegerList(num));
}
}
return result.stream().distinct().collect(Collectors.toList());
}
}최적화
최적화 시도 1
is_valid에서 0포함체크를 중복체크보다 먼저 수행한다. 0은 .contains(0)으로 확인 가능하지만 중복체크는 List에 distinct()를 수행한 뒤 다시 list로 collect한 뒤 확인 가능하기 때문이다.
private boolean is_valid(int num){
List<Integer> numarr=intarr_to_IntegerList(num);
//0이 있는지 체크
if(numarr.contains(0)){
return false;
}
//중복되는 수가 있는지 체크
int distinct_size=numarr.stream().distinct().collect(Collectors.toList()).size();
int origin_size=numarr.size();
if(distinct_size!=origin_size){
return false;
}
return true;
} 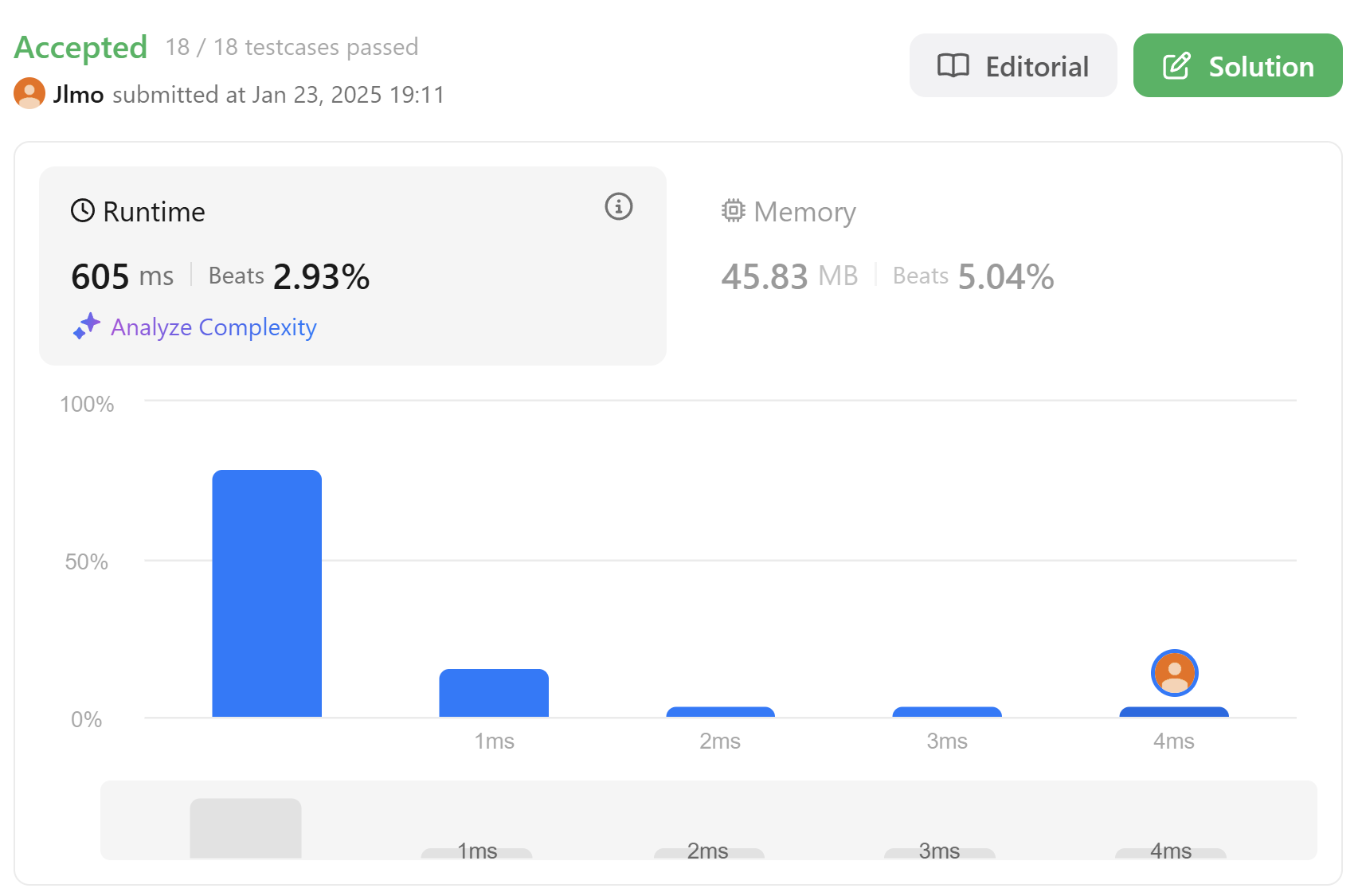
691ms->605ms로 시간복잡도가 감소하였다.
최적화 시도 2
더 이상 위 코드에서 최적화할 수 있는게 보이지 않아 정석적인 백트레킹을 적용해보자.
GPT를 돌려 코드를 작성시키고 제출해보았다.
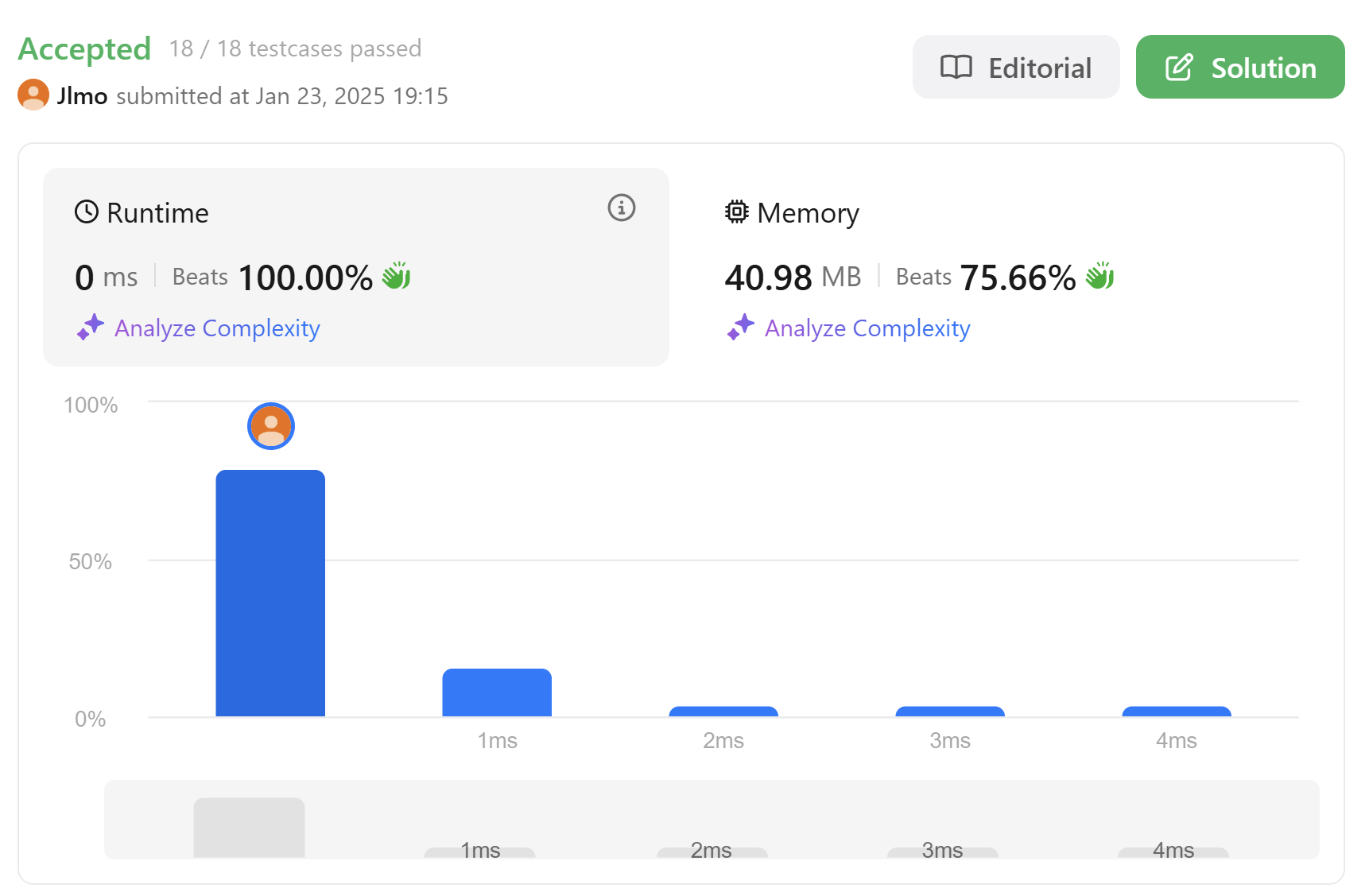
비교가 안될정도로 최적화가 이루어진 것을 확인할 수 있다. 코드를 리뷰해보자.
우선 드디어 이해하였다. 이전에는 조합의 경우를 구하려면 백트레킹이 필요하구나 라는 식으로 이해했어서 어려웠었는데, 백트레킹은 단순한 알고리즘 구조로 어떤 집합에 대해 특정 원소를 추가하고 연산한뒤 다시 추가하기 전으로 돌아가는 구조를 의미한다.
이해하기 쉽게 의사코드를 작성해보면
list.add(1)
list.something(1)
list.remove(1)
list.add(2)
...
의 구조이다.
이 방법이 왜 지금과 같은 조합의 경우를 구하는데에 사용되냐면 조합을
{1,2,3}
{1,2,4}
...
{1,2,9}
에서 다음
{1,3,4}로 가기위해서 index 2의 원소를 다루기 전에 다루었던 index 1의 원소로 다시 돌아가서 작업을 처리하고 이에 따라 index 2의 원소를 설정해야하기 때문이다.
다시 문제로 돌아가서, 위 문제를 해결하기 위해 결국 원소를 하나씩 List current에 추가할 것인데 이때 전체 배열의 관점이 아닌 원소별로 하나씩 문제의 조건을 확인하기 위하여 특정 숫자 start를 current에 추가하면 다음 재귀호출에서는 k를 -1한 값(방금 하나 current에 넣었으니)과 target-i(합이 되어야 하는 값에 방금 current에 넣은 값을 빼서 다음 작업 시 충족해야하는 sum값을 갱신)로, start+1을 통해 다음으로 확인작업을 수행할 값을 넣어준다.(123 다음 124니 이걸 부분적으로 봐서 3에서 4로 만드는 부분이 이 부분)
그리고 최종적으로 findCombinations를 재귀적으로 수행한 후 remove를 통해 방금 다룬 수를 지우고 다음 단계로 넘어간다. 젤 오른쪽 자리는 for(int i=start; i<=9; i++) 에서 다루고 그 외 앞자리들은 current.remove()를 통해 순차적으로 탐색됨.
GPT에게 부탁해 주석버전으로 설명된 코드는 아래와 같다.
class Solution {
/**
* k개의 숫자로 합이 n이 되는 조합을 찾는 메인 함수
*
* @param k 원하는 숫자 개수
* @param n 원하는 합
* @return 가능한 조합의 리스트
*/
public static List<List<Integer>> combinationSum3(int k, int n) {
// 결과를 저장할 리스트
List<List<Integer>> result = new ArrayList<>();
// 백트래킹 탐색을 시작 (1부터 시작하는 숫자 조합을 찾음)
findCombinations(k, n, 1, new ArrayList<>(), result);
// 최종 결과 반환
return result;
}
/**
* 재귀적으로 조합을 찾는 헬퍼 함수 (백트래킹)
*
* @param k 남아있는 숫자의 개수
* @param target 현재 남아있는 목표 합
* @param start 탐색을 시작할 숫자 (1부터 시작, 중복 방지 위해 증가)
* @param current 현재까지 구성된 조합
* @param result 모든 가능한 조합을 저장할 리스트
*/
private static void findCombinations(int k, int target, int start, List<Integer> current, List<List<Integer>> result) {
// 종료 조건 1: 숫자가 k개이고 목표 합이 0이면 현재 조합을 결과에 추가
if (k == 0 && target == 0) {
result.add(new ArrayList<>(current)); // 현재 조합을 복사해서 결과에 저장
return; // 더 이상 탐색하지 않고 종료
}
// 종료 조건 2: 숫자가 부족하거나 목표 합이 음수가 되면 탐색 종료(아래 start+1에서 10이 된다면 음수가 될 수 있음. 이를 거르기 위한 것)
if (k == 0 || target < 0) {
return;
}
// 현재 숫자부터 9까지의 숫자를 사용하여 조합 탐색
for (int i = start; i <= 9; i++) {
// 숫자 i를 현재 조합에 추가
current.add(i);
// 남은 숫자 개수를 줄이고, 목표 합을 줄여서 재귀 호출
// i + 1을 넘기므로 숫자가 중복되지 않음
findCombinations(k - 1, target - i, i + 1, current, result);
// 백트래킹: 재귀 탐색 후 마지막에 추가한 숫자를 제거
current.remove(current.size() - 1);
}
}
} ```