(24.11.30)
- 문제: 사람을 고용할 때 필요한 가격이 int[] costs, 고용해야하는 인원수가 k, 그리고 candidate인자가 뭘 하는지 잘 이해가 안된다.
인덱스가 바뀔 때와 상관없이 고정적으로 candidates로 전달된 index는 작업자로 선택하면 안되는 것인가?
공감하는 바이다.
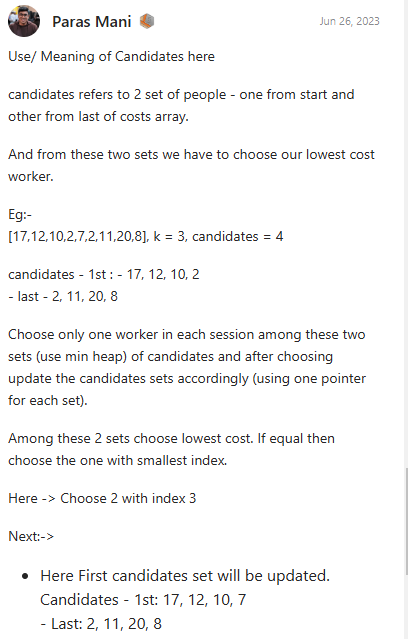
잘 설명해주신 discussion이 있어 이해하였다. new int[10]배열에서 candidate가 2면 0, 1, 8, 9중에서 싼 값을 선택하라는 의미라고 한다. 코드를 작성해보자. 어떻게 작성하면 1트에 끝낼 수 있을까?
k만큼 작업자를 고를 것이니 for로 돌리고, 그 안에 candidates for를 이용해 앞뒤로 접근하면 될 듯 하다. 또한 문제에서는 작업완료된 원소를 삭제시키는데, 비용최소화를 위해 -1값으로 바꾸어 -1인 경우 넘기는 방법이 어떨까.. 이를 상수화해서 가독성을 높이자. 안쪽 for 루프 돌기전에 가격이 싼 min을 설정해서 루프 탈출 후 -1처리하면 될 듯 하다. 여기서 중요한 것은 범위가 겹치는 지점인데, 범위가 겹치는 경우에는 인덱스가 서로 엉킬 수 있기 때문이다. 엉키는 지점에서는 flag를 설정하여 루프를 탈출시킨 뒤 하나의 인덱스로 접근하면 코드가 길어질 수 있어도 로직이 단순해 질 것으로 보인다. 이러면 단순히 헤아려도 변수가 5개, 6개는 될 듯 하니 변수 네이밍과 인덱스 설정을 유의해야 할 듯 하다. (혹시 범위가 엉킬 때 더 좋은 방법이 있을까? 애초에 인덱스를 하나만 사용한다면? 오히려 좋을 듯 하다. 0~candidates-1과 length-candidates+1~length니까 length-candidate*2만큼 +하면 될 듯 하다. 만약 엉키는 경우엔 어차피 인덱스 1개라 0~length를 돌리면 될 듯 하다. 인덱스 break한 뒤 사용할 수도 있으니 인덱스 변수 초기화는 루프 들어가기 전에 해두자.
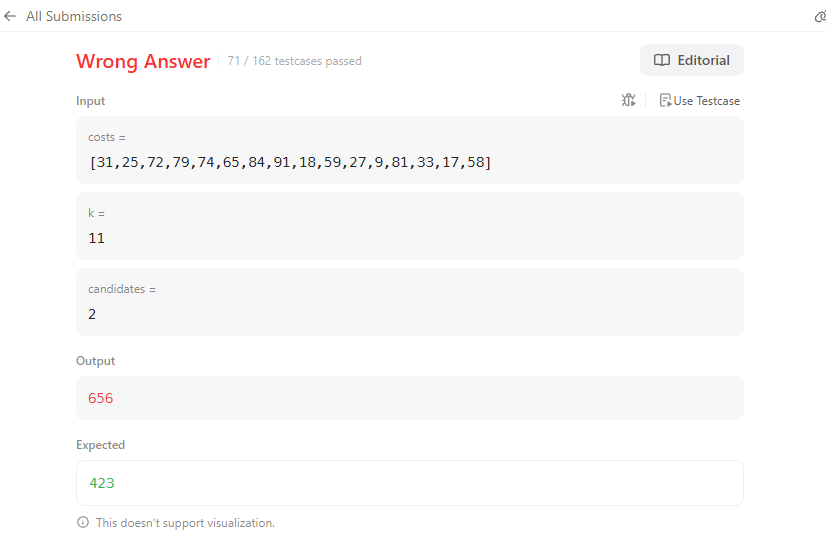
(24.12.02)
생각보다 쉽지 않다.. -1로 치환해서 효율성을 올리며 candidate범위만큼 선정하는게.. 고로 Linkedlist를 사용해 실제 삭제를 수행해보았다.
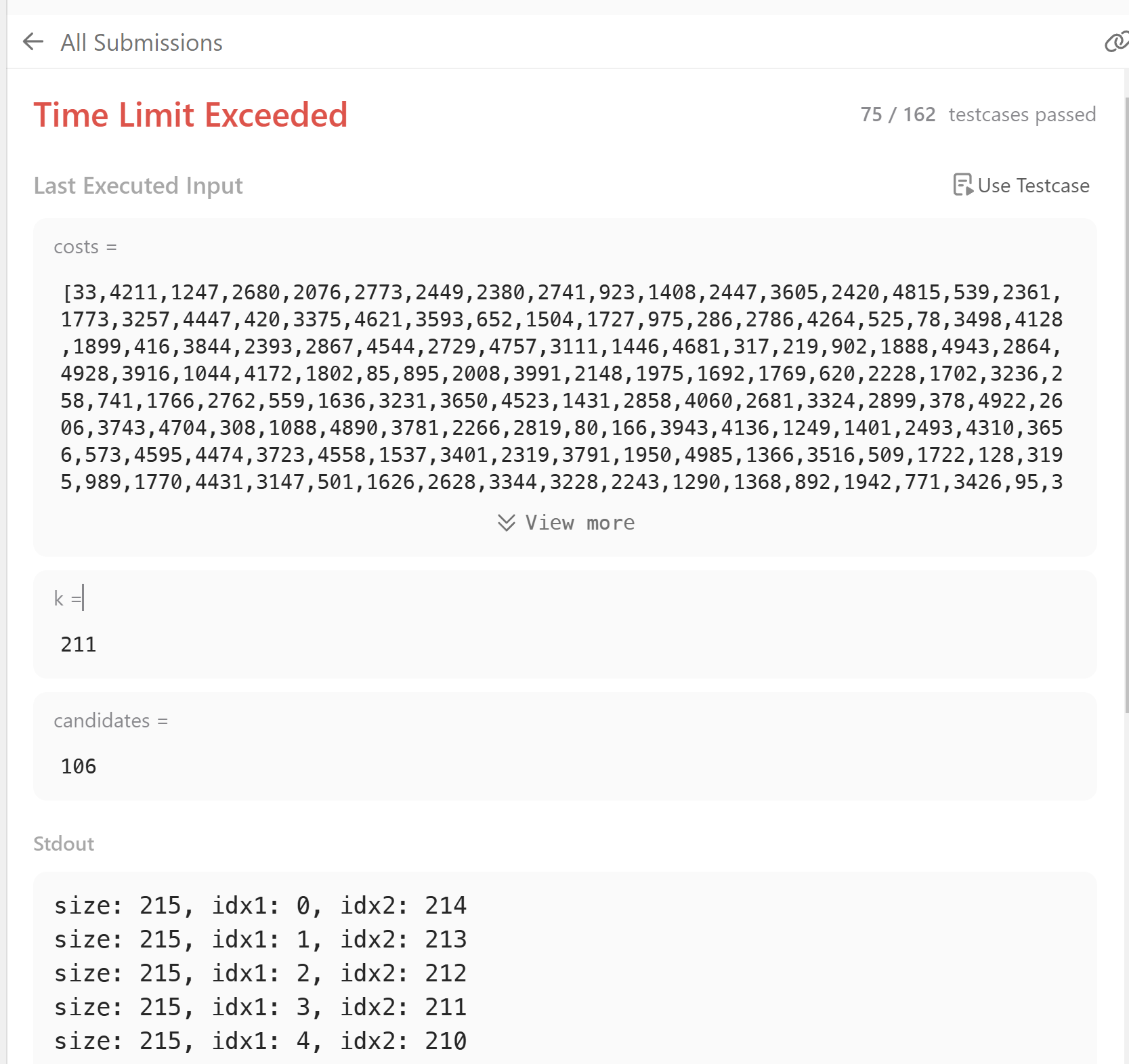
아무래도 배열에 직접 접근해야할 듯 하다.
public long totalCost(int[] costs, int k, int candidates) {
final int MAX_COST=10000;
int LENGTH=costs.length;
int min_cost, result_cost=0, partial_min_index=-1;
for(int i=0; i<k; i++){//추출해야하는 워커 별 루프
//0~candidates, LENGTH-candidates~LENGTH-1 중에서 최솟값 선정
//비용 반영 및 -1화. 만약 bidirectional linked list라면?
min_cost=MAX_COST;
int front_index=0, rear_index=LENGTH-1;
for(int j=0; j<candidates; j++){
for(; front_index<LENGTH; front_index++){
if(costs[front_index]!=-1){
break;
}
}
if(costs[front_index]<min_cost){
min_cost=costs[front_index];
partial_min_index=front_index;
}
for(; rear_index>=0; rear_index--){
if(costs[rear_index]!=-1){
break;
}
}
if(costs[rear_index]<min_cost){
min_cost=costs[rear_index];
partial_min_index=rear_index;
}
}
result_cost+=min_cost;
costs[partial_min_index]=-1;
System.out.println("added "+min_cost+" of "+partial_min_index);
}
return result_cost;
}(24.12.03)
좀 더 배열 접근을 단순화할 수 있을 것 같다. 지금의 방법은 너무 가독성이 떨어져 쉽게 디버깅을 할 수 없다. 코드를 리팩터링 한 뒤 디버깅을 수행하였다.
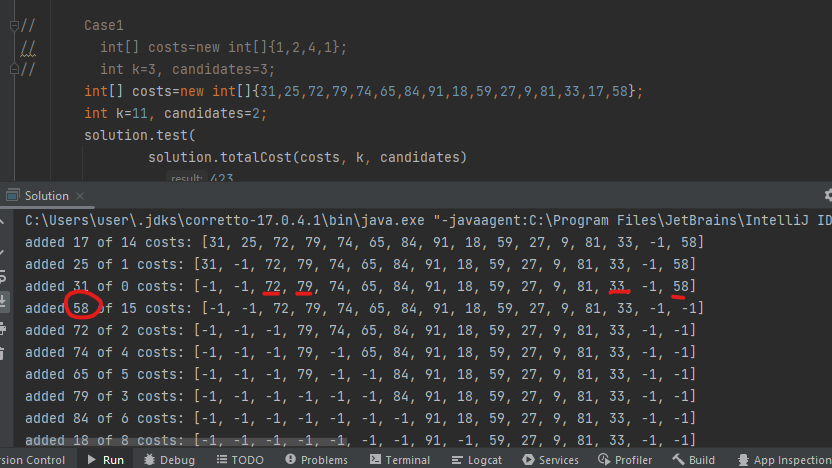
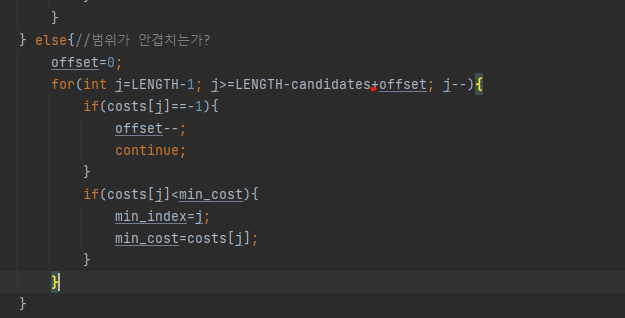
offset 부호가 바뀌어있었다.
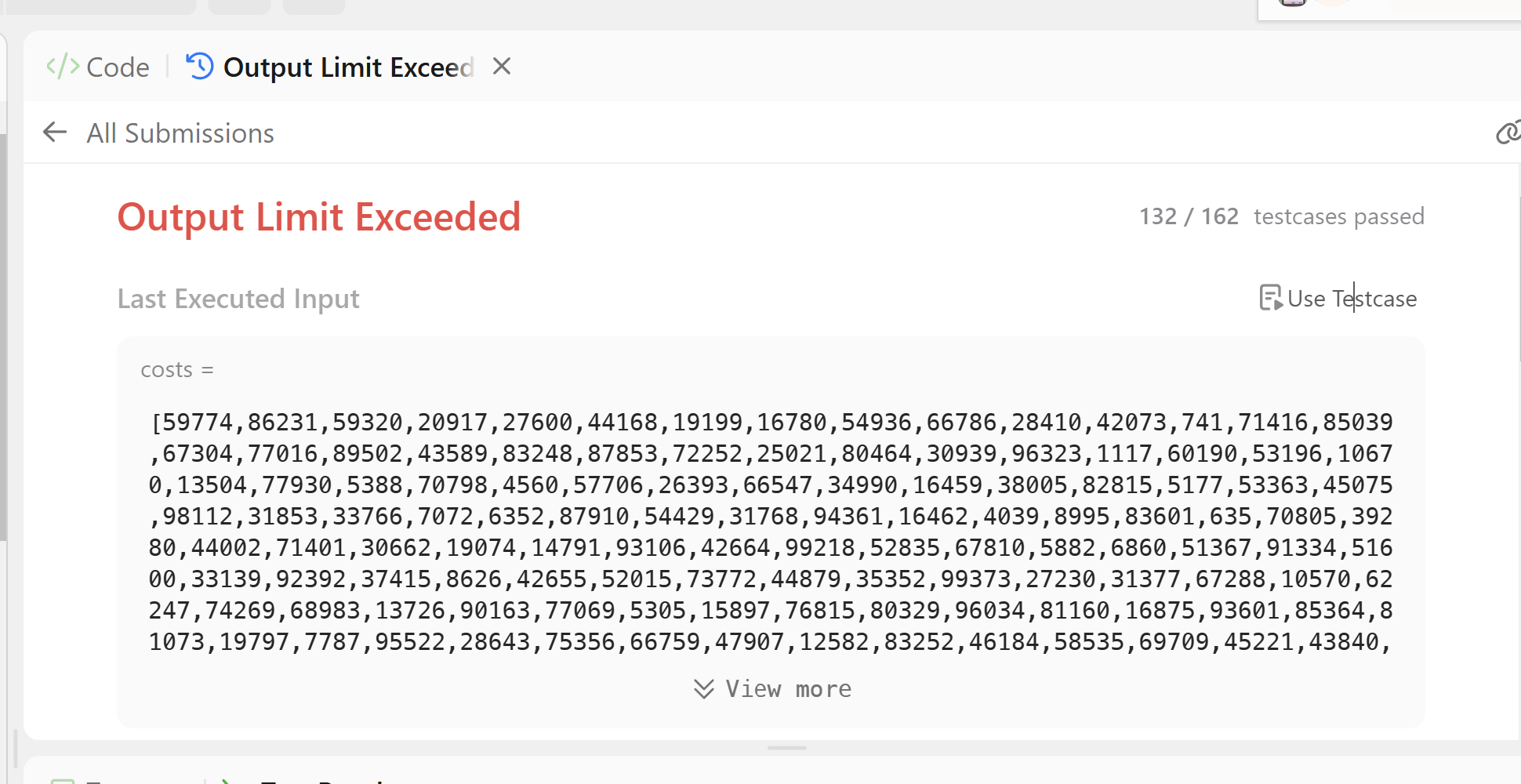
sout출력 주석 후 테스트 케이스로 돌려보니 TLE가 발생하였다. 최적화를 진행해보자. 현재로 73번대에서 TLE가 발생하여 최적화를 진행한 것이기에 이 방법을 고수하는 것 보단 이전 문제에서 사용했던 priority_queue를 사용하면 좋지 않을까 싶다.
간단한 로직은 다음과 같다. 값을 비교 후 index를 pq에 저장한다. 이때 pq에는 candidate*2크기를 유지하며 최솟값 판단 후 최솟값을 deque하고 해당 방향의 원소를 하나 더 enqueue한다. 이때 같은 값의 경우 앞 index가 먼저 나와야 하기에 이를 따로 처리해줘야 한다(index값 기준) 문제는 범위가 겹칠 때 이다. 범위가 겹치는 경우에도 돌아가야하기에, 크기 규정 없이 로직으로 크기가 맞춰지게 구성하거나 그 때를 따로 빼내어 전체 값 중 최솟값을 고르는 방식으로 진행해야할 듯 하다.
(24.12.04)
최적화 진행중
(24.12.07)
24.12.03에 생각한 방식으로 토대를 작성해보았다.
public long totalCost(int[] costs, int k, int candidates) {
int LENGTH=costs.length;
int cost=0;
PriorityQueue<Integer> minHeap=new PriorityQueue<>(
(a, b) -> Integer.compare(costs[a], costs[b])//인덱스에 해당하는 원소 값을 이용해 정렬
);
//초기 candidate만큼 minHeap에 넣음.
for(int j=0; j<candidates; j++){
minHeap.add(j);
if(j<LENGTH-1-j) {//안겹치게끔
minHeap.add(LENGTH - 1 - j);
}
}
int removed_index;
for(int i=0; i<k; i++){// k명을 추출.
removed_index=minHeap.remove();
cost+=costs[removed_index];
//누굴 넣을까?
}
return cost;
}현재 고민중인 것은 누굴 넣을까?에 대한 고민이다. 제거한 값의 인덱스의 앞뒤를 생각해보자. 왼쪽 candidate범위라면 candidate가 2이상이라는 경우에서 제거값 인덱스 -1이 이미 minHeap에 contain이다. 만약 candiate가 1이라면? peek한 값보다 작으면 왼쪽 범위이다.
위 방식을 구현해보면 아래와 같다.
class Solution {
public long totalCost(int[] costs, int k, int candidates) {
int LENGTH=costs.length;
int cost=0;
PriorityQueue<Integer> minHeap=new PriorityQueue<>(
(a, b) -> Integer.compare(costs[a], costs[b])//인덱스에 해당하는 원소 값을 이용해 정렬
);
//초기 candidate만큼 minHeap에 넣음.
for(int j=0; j<candidates; j++){
minHeap.add(j);
if(j<LENGTH-1-j) {//안겹치게끔
minHeap.add(LENGTH - 1 - j);
}
}
int removed_index;
boolean is_left=true;
List<Integer> removed_indexes=new ArrayList<>();
for(int i=0; i<k; i++){// k명을 추출.
removed_index=minHeap.remove();
cost+=costs[removed_index];
removed_indexes.add(removed_index);
//누굴 추가할까?
if(candidates>1){
if(removed_index-1>=0 && (minHeap.contains(removed_index-1) || removed_indexes.contains(removed_index-1))){ // 왼쪽 범위
is_left=true;
} else if(removed_index+1<LENGTH && (minHeap.contains(removed_index+1) || removed_indexes.contains(removed_index+1))){// 오른쪽 범위
is_left=false;
}
} else { //candidate == 1 인 경우
if(minHeap.peek()>removed_index){// 왼쪽 범위(empty는 없음. 짝수로 후보자 들어가기에)
is_left=true;
} else if(minHeap.peek()<removed_index){// 오른쪽 범위
is_left=false;
}
}
if(is_left){
if(removed_index+1<LENGTH && !minHeap.contains(removed_index+1)) { // 안겹치니
minHeap.add(removed_index + 1);
}
} else {
if(removed_index-1>=0 && !minHeap.contains(removed_index-1)){ // 안겹치니
minHeap.add(removed_index-1);
}
}
}
return cost;
}
}다만 이 방식은 인덱스가 0 혹은 LENGTH-1일 경우 -1과 +1로 판단하기 어렵다는 한계가 존재한다.
어떻게 하면 minHeap을 잘 사용할 수 있을지 GPT를 이용해 코드를 완성시켜보았다. GPT는 위 문제를 아주 쉽게 해결하였는데, 초기 candidate만큼 minHeap을 초기화시킬 때 left와 right 경계를 따로 변수로 두고, left보다 작으면 왼쪽값이므로 left+1을 추가했다. 코드를 최적화 할 때, 변수를 하나 더 두면 간단해질 수 있다는 점과 최적화 하려는 부분의 코드만 생각하는 게 아닌 그 전에 거치는 코드를 최적화하여 문제를 해결할 수도 있다는 배움을 얻었다.
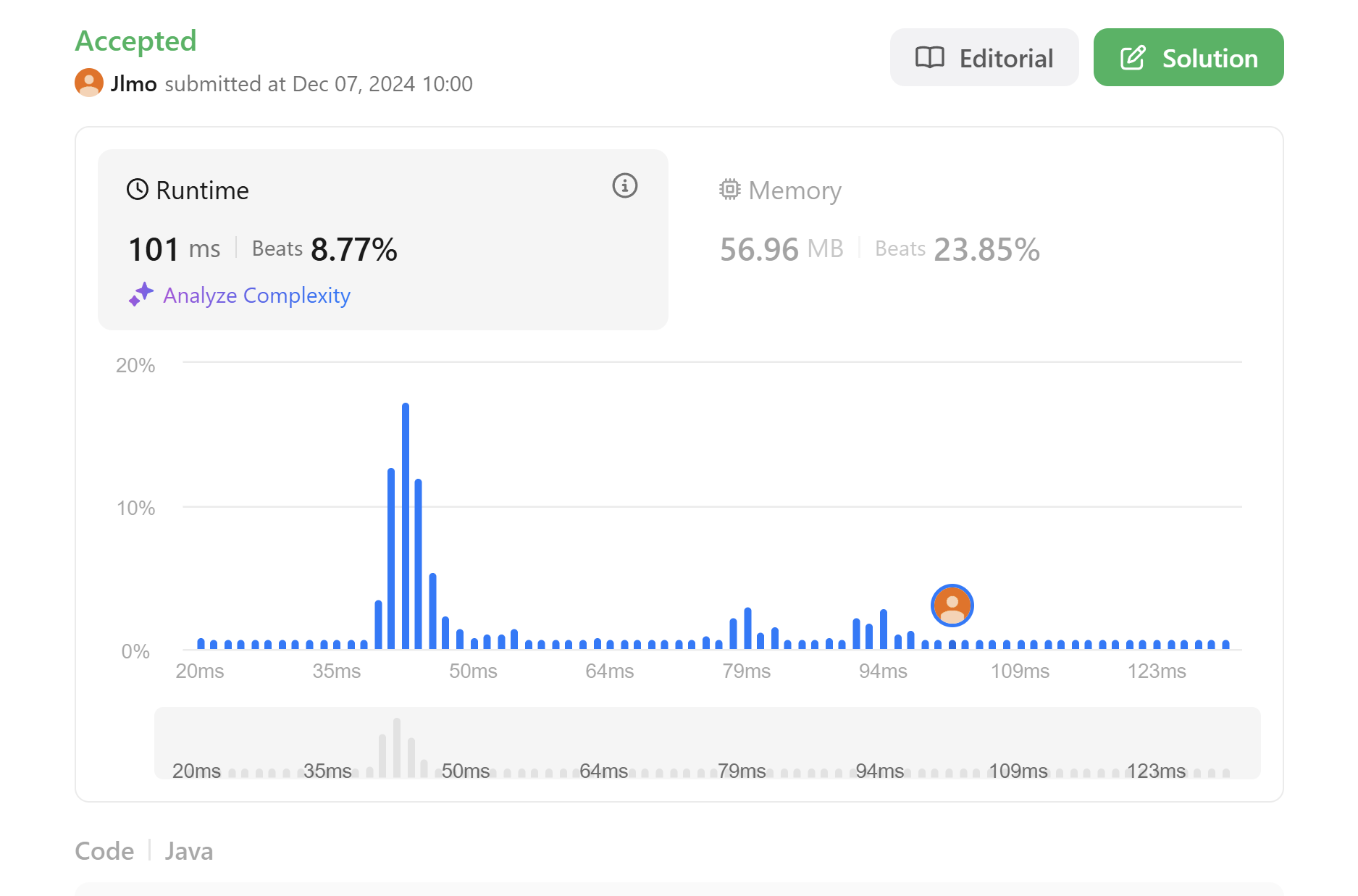
뛰어난 복잡도를 기록한 사람들의 코드는 어떻게 설계했을까?
candiate범위 앞 뒤 별로 heap을 별도로 만들고, 마찬가지로 경계를 의미하는 start와 end변수를 두었다. while을 이용해 k--하며 k번을 추출하는데, heap.size()와 candiate비교 및 start와 end를 비교하여 부족한 범위의 원소를 추가시켜 내가 곤란해하던 문제를 해결하였다. 비용 계산은 heap 두개를 peek하여 최솟값을 찾아 비교하였다.
그 결과 내가 생각했던 방식보다 2배 이상 빠르게 작동하였다. 공간복잡도를 신경쓰지 말자. 약간 최적화한답시고 변수 1개로 모든 일을 처리하려하는 것은, heap 1개로 모든일을 처리하려 하는 것은 생각보다 효율적인 결과를 가져오지 않는 듯 하다. 최소한 기존 코드를 작성하며 TLE가 발생했을 경우 공간을 이용하여 이를 해결하는 접근이 필요하다.
