(25.01.04)
-
문제 이해
고릴라는 여러 상자에 담긴 바나나들을 효율적으로 먹을거다. 문지기가 h시간동안 자리를 비울 때, 시간당 k개의 바나나를 먹을거다. 이때 k개보다 적은 바나나가 상자에 남게되면 그 시간동안 안먹는다. 다 먹을 수 있는 최소의 k를 리턴하라. -
문제 접근
원소의 순서를 고려할 필요는 없어보인다.
piles[i]/k의 올림값의 합이 h이하이면 된다. 최소값을 구해야하니 k를 1부터 max(piles)까지 위 조건을 만족하는지 하나하나 반복문으로 확인시키자. 만약 max(piles)를 넘어서면 불가능하지만 해당 케이스는 문제 케이스에 없을 듯 하다.
class Solution {
public int minEatingSpeed(int[] piles, int h) {
int hour, max=Arrays.stream(piles).max().getAsInt();
for(int k = 1; k<=max; k++){
hour=0;
for (int i = 0; i < piles.length; i++) {
hour += Math.ceil(piles[i] * 1.0 / k);
}
if(hour<=h){
return k;
}
}
return -1;
}
}
TLE가 발생하였다.
어떻게 최적화를 할 수 있을까? 사실 반복문을 이용한 방법은 효율이 많이 떨어질 수 밖에 없다.
가장 간단한 방법인 반복문에 배열의 최저, 최대값을 이용해봤지만 TLE가 발생한 케이스는 최솟값보다도 작은 k값을 가진다.
(25.01.07)
이진탐색 힌트를 얻었다.
구해야하는 k가 8이 되는 경우를 기준으로 두고 1과 max값 사이에서 이진탐색을 진행하면 될 듯 하다. 최소가 되는 k를 구하려면 k일 때의 시간의 합이 h가 되면 된다.
class Solution {
public int minEatingSpeed(int[] piles, int h) {
int hour;
int length=piles.length;
int max=Arrays.stream(piles).max().getAsInt();
int start_k=1, end_k=max;
int mid_k=(start_k+end_k)/2;
while(true){
hour=0;
for(int i=0; i<length; i++){
hour+=Math.ceil(piles[i]*1.0/mid_k);
}
if (hour==h) {
break;
} else if (hour<h){
end_k=mid_k-1;
} else{
start_k=mid_k+1;
}
mid_k=(start_k+end_k)/2;
}
return mid_k;
}
}
이진탐색으로 같은 testcase 시도해봤는데 TLE가 발생하였다. 이진탐색에 추가적으로 최적화를 진행해야할 듯 하다.
piles를 정렬할 필요는 없어보이는데.. k에 따른 hour이 달라지기에.. 우선 최대한 이진탐색을 최적화해보자.
1. 정수 올림 최적화 (a+b-1)/b
여전히 해결되지 않았다. GPT를 통해 최적화해보니 이진탐색의 기본 종료조건은 start<=end꼴이고 이 꼴이 가장 효율이 좋고, 현재 mid의 초기화가 2번 이루어진다고 이를 최적화 하였다. 또한 반복문에서 iterator를 사용하였다.
내 코드에서 아쉬운 점은 mid값을 기준으로 판단한 뒤 start를 mid+1 혹은 end를 mid-1로 옮긴 것이다. 이 부분에서 성능저하가 되는 이유는 컴퓨터는 while(true){}로 지정되어있다고 조건확인을 건너뛰는게 아니라 절차적으로 true인가?를 확인하고 넘어간 뒤 내부의 if(mid==h)를 확인하는 총 두번의 조건 확인이 수행된다.
이와 반대로 이진탐색의 정석방식이라고 하는 while(start<end)는 위의 두번의 조건확인을 한번의 조건확인으로 최적화가 가능하게 된다.
또한 개인적으로 while(front<end)방식은 front가 괜히 end와 역전될 것 같은 느낌에 거부감이 드는데, 실제로 이진탐색을 수행하며 조건이 깨질 때는 +1 -1단위로 mid값 갱신이 수행되어 front==end인 경우일 뿐이라 이진탐색이 완료된 직후 start를 반환하던 end를 반환하던 이진탐색 값이 나오게 되어 더 안정적이다.
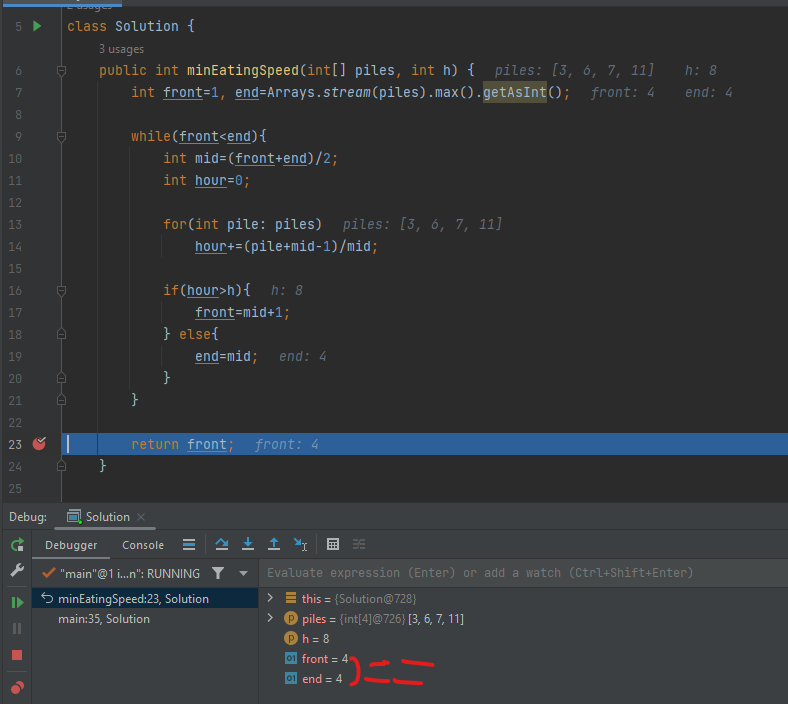
이러한 이유로 최적화를 위한 이진탐색에서는 조건 확인을 한 번만 수행하며 start와 end의 값이 일관적인 while(start<end)이 성능 효율성으로나 직관적으로나 좋다.
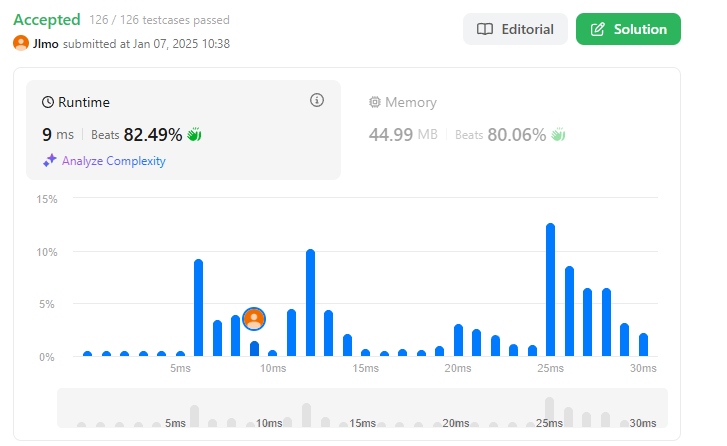
추가적으로 더 뛰어난 사람의 코드를 보았다.
class Solution {
public int minEatingSpeed(int[] piles, int h) {
int n = piles.length;
long total = 0;
for (int p : piles) total += p;
// 이진 탐색을 보다 최적화 하기 위해 최소 탐색 시간과 최대 탐색 시간을 수학적으로 계산하여 범위를 선정
int left = (int) ((total - 1) / h) + 1; // 모든 시간을 효율 적으로 탐색하였을 때의 최소 k (모든 바구니에 딱딱 k개씩 나누어 떨어지면)
int right = (int) ((total - n) / (h - n + 1)) + 1; // 각 pile을 최대한 분산시켰을 때의 최대 k (모든 바구니에 k개씩 나눠도 나머지가 있다면)
while (left < right) {
int mid = left + (right - left) / 2; // 오버 플로우 방지를 위해. 같은 mid값 계산인 것은 똑같음.
int time = 0;
for (int p : piles) {
time += (p - 1) / mid + 1;
}
if (time > h) {
left = mid + 1;
} else {
right = mid;
}
}
return left;
}
}이 코드는 여기서만 정리하고 넘어가려했는데, git에 마찬가지로 push해야겠다. 코드가 너무 좋다.
이진탐색을 극한으로 최적화하기 위해서 탐색 범위를 수학적 계산으로 최악의 경우, 최적의 경우를 고려하여 left와 right의 초기값을 선정했고, 같은 mid값 계산에 (left+right)/2는 큰 수의 경우 left+right에서 정수 오버플로우가 발생할 수 있다는 문제를 해결하기 위해 left+(right-left)/2로 안정성을 높였다.
