오늘 할일
1. Project-X 과제 완료
2. 사상의학 과제
3. 데이터통신&운영체제 공부 시작
4. SK C&C 활동참여인증서 알아보기
오늘 한일
1. Project-X 과제4번, 과제 5번
과제 5번 퀵정렬 시 상당히 디버깅에 애를 먹었는데, 퀵정렬에 대한 기본적인 이해가 먼저 부족했던 점이 가장 큰 요인이었던 것 같다.
퀵정렬은 총 5가지의 변수를 사용한다. 재귀를 위한 리스트의 범위를 알려주는 left, right 그리고 좌측의 배열과 우측의 배열을 각각 순회하며 사용할 인덱스 low, high 그리고 pivot이 필요하다.
pivot은 코드에 따라 다르나 left혹은 right값을 사용한다.
전체적인 퀵 정렬의 구조는 아래와 같은 재귀구조를 띈다.
quickSort(arr, left, right){
int pivot=partition(arr, left, right);
if(left<pivot-1)
quickSort(arr, left, pivot-1);
if(pivot+1<right)
quickSort(arr, pivot+1, right);
}먼저 partition에서 pivot을 기준으로 좌측에는 pivot보다 작은 값, 우측에는 pivot보다 큰 값이 들어가게 정렬한다. 그 후 pivot의 위치를 중앙으로 옮겨주고 그 위치를 리턴하여 좌우정렬된 기준 인덱스 값을 얻는다.
다음으로는 pivot값을 기준으로 배열을 분할하여 마찬가지의 방법은 각각의 배열에서 수행한다.
재귀함수를 호출할 때, left가 right보다 커져서 꼬이는 경우를 막기 위해 if문으로 호출 전 값의 범위를 체크하게 하였다.
Partition함수의 구조는 아래와 같다.
partition(arr, left, right){
int pivot=target.get(left);
int low=left+1;
int high=right;
while(low<=high) {
while(low<=right && pivot>target.get(low))
low++;
while(left<=high && pivot<target.get(high))
high--;
if(low<=high)
listSwap(target, low, high);
}
listSwap(target, left, high);
return high;
}첫번째로는 아무 값이나 pivot값으로 설정한다. 다음으로 pivot기준으로 정렬될 좌 우 배열 접근을 위한 low와 high를 세팅해준다. 이 때 low를 left+1로 정하는 이유는 pivot값을 제외하기 위함이다.
두번째로는 좌측 배열에서 pivot보다 큰 값의 index를 찾아내고, 우측 배열에서는 pivot보다 작은 값의 index를 찾아낸다. swap을 진행하기에 앞서 low<=high인지 즉, 다른 배열범위를 침범한 인덱스가 아닌지 확인하고 swap을 진행한다. while문을 돌다 pivot기준으로 정렬이 완료되면 while문을 탈출한다.
세번째로는 pivot값을 실제로 옮겨준다. while문을 탈출하는 시점에서 low<high즉, high는 왼쪽 영역에 마지막, low는 우측 영역의 첫번째에 있다. pivot값은 본래 left값이기에 왼쪽 영역 배열의 마지막 값(high_현재 high<low)과 swap을 진행한다. 그 후 좌우정렬된 기준인 pivot의 인덱스를 리턴하여 어느 위치를 기준으로 배열이 되었는지 partition을 리턴해준다.
여기서 특히 햇갈렸던 경우는, 옮겨야하는 값이 홀수일 때다. 짝수인 경우 딱딱 알맞게 low와 high가 swap되지만 왼쪽 배열의 값 하나가 pivot보다 큰 상태에서 우측 배열은 이미 정렬이 완료되었다면 어떻게 처리될까? 결론은 마지막에 처리된다. low와 high가 각각 이동하다가 남은 하나의 값을 low가 가리키고, high가 low+1값을 가리키는 상황에 도달했다고 하자(즉, 현재 low와 low+1의 경계가 partition). 그러면 while문은 pivot값의 범위 조건에 따라 escape되고, if(low<=high)이기에 이 둘은 swap된다. 다르게 말하면 partition의 경계가 --된다는 의미이다.
다시 말하면 partition의 우측배열의 첫번째 값과 좌측배열의 마지막 값이 swap되어 옮겨야 하는 값이 홀수 일 경우에도 정상적으로 자리를 찾아가게 된다.
문제 자체는 해결했지만, 언제봐도 햇갈리는 정렬인 것 같다.
다른 코드를 살펴보니 while조건문에 선제조건을 없애고 구현한 코드가 있던데, 최대한 내 코드에 맞추어 수정해보아도 오류가 발생한다..
과제6번
Median of two sorted array문제로 두개의 배열을 입력받아 중앙값을 계산하는데, 복잡도 O(logn)으로 해결해야하는 문제이다. 간단한 수학적 지식이 사용되지만 그 어디에서 간단하게 설명한 곳이 없다. 유명한 문제인 만큼 조금만 정리하면, 두 배열의 중앙값을 계산하기 위해서 각각 아무 값이나 i와 j로 둬보자. 첫번째 배열의 인덱스 i와 두번째 배열의 인덱스 j를 기준으로 했을 때, i보다 큰 값들이 전부 j보다 작다면 중앙값은 첫번째 배열의 i~ 그리고 두번째 배열의 ~j안의 범위에 있을 것이다. 고로 중앙값에 해당하는 값의 범위를 좁히면 중앙값의 범위를 i, j-1 그리고 i+1, j로 줄일 수 있다. 이때 i-1,j-1의 최댓값을, i와j의 최소값을 구한 후 전체 길이가 짝수인 경우 max값을, 홀수인 경우는 max와 min의 평균값을 반환시키면 된다.
코드 구현은 비교적 간단한 편이지만 이론을 이해하기에 어려움이 있었다. 왜냐하면 이러한 개념을 누가봐도 이해하기 어렵게 아래와 같이 작성했기 때문이다.
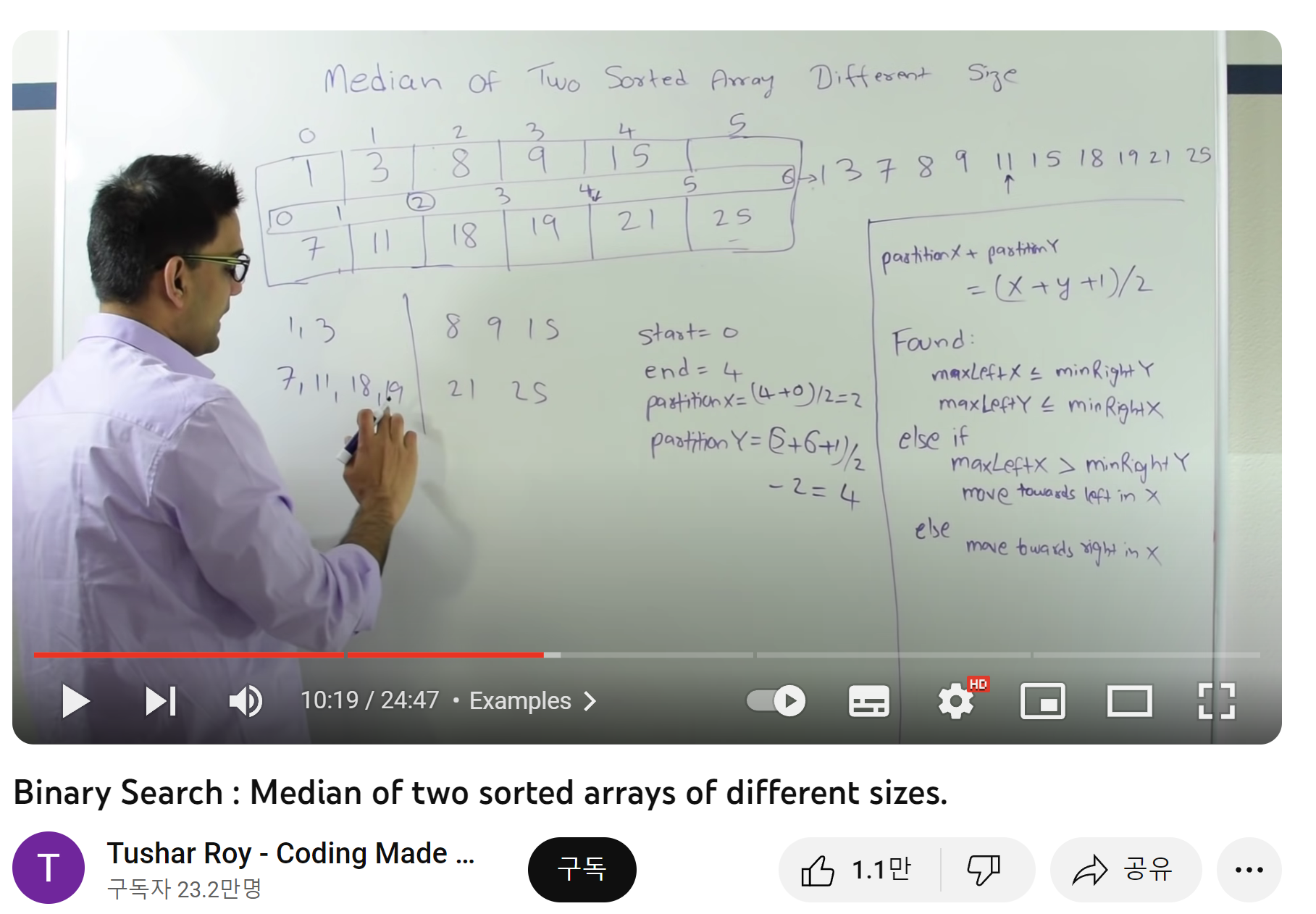
전체 아이디어를 얼추 이해한 뒤 실제 코드를 보며 완전히 이해하였다. 다음은 찾아낸 가장 간단한 설명이다. https://izmirprogramming.tistory.com/11 다음은 해당 블로그를 참고하여 자바로 작성한 코드이다.
private static double getMid(int[] array1, int[] array2){
if(array1.length>array2.length)
System.out.println("swap?");
int n=array1.length;
int m=array2.length;
int left=0, right=n;
while(left<=right){
int i=(right-left+1)/2+left;//왼쪽 배열의 좌우기준값
int j=(n+m+1)/2-i;//우측 배열의 좌우기준값_공식을 통해 도출
int array1_1=i>0?array1[i-1]:Integer.MIN_VALUE;
int array1_2=i<n?array1[i]:Integer.MAX_VALUE;
int array2_1=j>0?array2[j-1]:Integer.MIN_VALUE;
int array2_2=j<m?array2[j]:Integer.MAX_VALUE;
//[2, 30, 10] [42, 1, 40, 27, 9]
if(array1_1>array2_2) {
right = i - 1;
} else if(array2_1>array1_2){
left=i+1;
} else{
int leftMax=Integer.max(array1_1, array2_1);
int rightMin=Integer.min(array1_2, array2_2);
if((n+m)%2!=0)
return leftMax;
else
return (leftMax+rightMin)/2.0;
}//1, 2, 9, 10, 27, 30, 40, 42
}
return 0.0;
}과제7번
mergeSort()를 구현하는거라 위의 quickSort보단 쉬웠지만, 문제는 Frequency(빈도수)를 고려해야하는 문제였다. 일반적인 mergeSort가 아니라 frequency를 추가적인 기준으로 mergeSort를 진행해야했기에 원리는 이해했지만 기본적인 코딩 능력이 필요한 시점이었다. 꽤 걸리긴 했지만 보너스 문제까지 진행하여 해결하였다. bubbleSort를 통해 구현하는 기본 문제는 swapWithFrequency라는 함수를 두어 비교적 쉽게 해결하였고, mergeSort를 통해 구현하는 보너스 문제는 buffer와 frequencyBuffer를 두어 해결하였다. 버블은 시간복잡도가 O(n^2)이고 합병정렬은 O(nlogn)이다. 이진탐색과 같이 중간을 나누어 보기에 높이는 logn을 가지게되고, 그러한 반복 과정을 merge()함수에서 n만큼 수행하여 O(nlogn)이다.
과제8번
Queue구현은 쉽게 해결하였다.
