오늘 할일
1. 도커 공부
2. LeetCode
오늘 한일
1. LeetCode
- Reorder Routes to Make All Paths Lead to the City Zero을 재도전해보자. 힌트를 열람했는데, 방식이 같다. 방향은 맞는데 알맞게 최적화만 진행되면 될 듯 하다. 시간 최적화를 위해 시도해 볼 첫번째는 메모리 할당 시간을 줄이는 것이다. 현재 시간을 줄이고자 배열로 queue를 구현하여 사용하고 있다. 이 경우
int[] indexes=new int[connections.length*2];
int[] list=new int[connections.length*2];부분에서 불필요한 공간까지 할당될 뿐더러, dequeue시 앞 부분의 공간이 낭비된다는 단점이 있다. 필요한 만큼만 할당되게끔 Queue API를 사용해보자. 변경한 부분은 2가지로 indexes를 int[][]에서 queue로, list를 int[]에서 List로 변경하였다.
class Solution {
public int minReorder(int n, int[][] connections) {//n은 노드의 개수, connections는 a->b방향관계
int result=0, iList=0;
int index, target_index, target_val, i;
Queue<Integer> indexes=new LinkedList<>();
List<Integer> list=new ArrayList<>(connections.length);
for(int[] conn: connections){
list.add(conn[0]);
if(conn[0]==0)
indexes.add(iList);
iList++;
list.add(conn[1]);
if(conn[1]==0)
indexes.add(iList);
iList++;
}
//0부터 시작해서 DFS진행
while(!indexes.isEmpty()){
index=indexes.remove();
if(index%2==0) {//짝수라면 시작지점
result++;
target_index=index+1;
} else{//홀수라면 도착지점
target_index=index-1;
}
target_val=list.get(target_index);
list.set(target_index, -1);//현재 index와 같이 처리한 쌍의 데이터 무시를 위함
for(i=0; i<list.size(); i++)
if(list.get(i)==target_val)
indexes.add(i);
}
return result;
}
}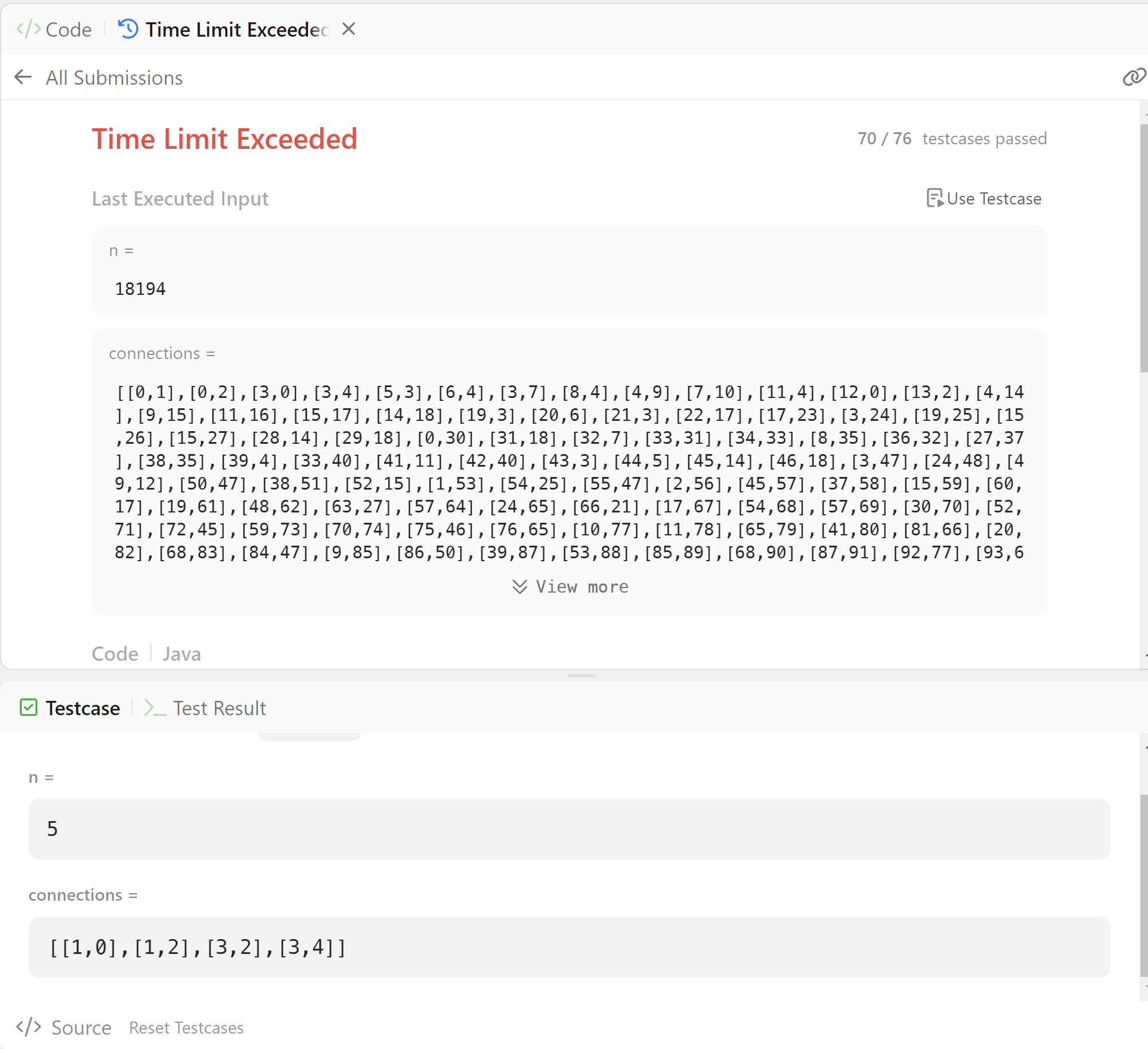
오히려 71번테스트까지 가지 못하고 70번에서 TLE가 발생하였다.
queue로 바꾸며 같이 변경한 list는 생각해보니 매번 add할 때 마다 추가가 발생해야하기에, initial capacity를 connections.length에서 connections.length*2로 변경해주었다.(모든 관계가 들어가야 하기에 애초에 전체 사이즈를 할당) 그 결과 70 번 테스트를 넘어 71번 테스트케이스에 도달하였다.
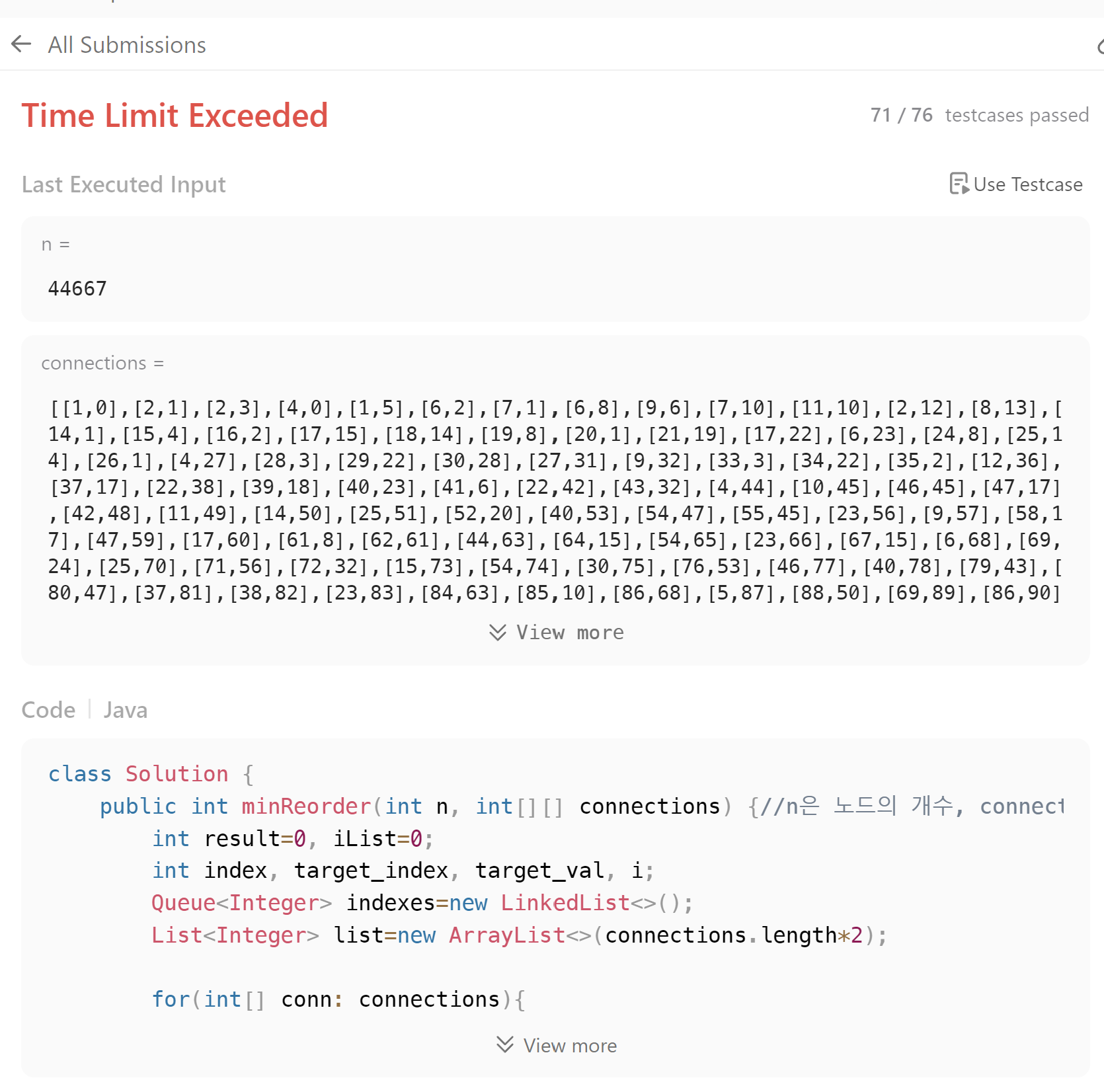
최적화를 더 수행하기 위해 list변수를 int []로 바꾸어보았지만, 여전히 통과하지 못했다.
while 안에서 이미 처리된 connections 쌍의 나머지 값인 경우 continue로 예외처리되게 하였지만 여전히 통과하지 못했다.
코드를 천천히 검토해보다가, 이중 for문을 발견했다.
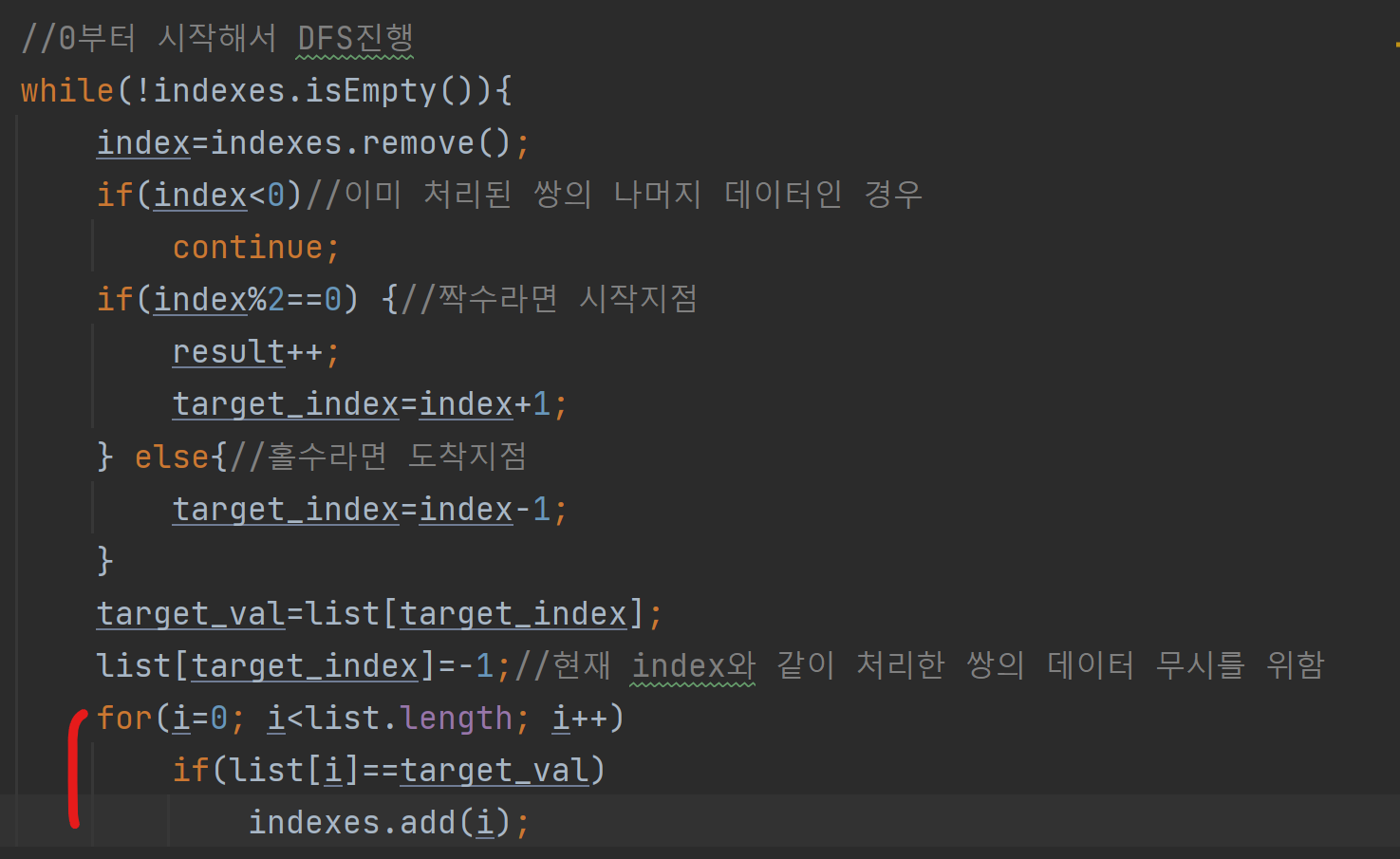
이 부분은 DFS를 수행중인 노드 index값의 쌍이 되는 나머지 값의 index들을 전부 찾아 queue에 enqueue하는 과정이다. 요약하면, 특정 값을 전체 list에서 찾아 해당하는 인덱스를 골라내는 과정이다.
GPT를 사용해 stream 형식으로 변경해보았지만 오히려 느려져 69번 테스트 케이스에서 걸리고 말았다.
int finalTarget_val = target_val;
indexes.addAll(IntStream.range(0, list.length)
.filter(j -> list[j] == finalTarget_val)
.boxed()
.collect(Collectors.toList()));진짜 도저히 모르겠어서 GPT에게 내 코드를 최적화해달라고 맡겨보았다.
class Solution {
public int minReorder(int n, int[][] connections) {//n은 노드의 개수, connections는 a->b방향관계
int result=0, iList=0;
int index, target_index, target_val, i;
Queue<Integer> indexes=new LinkedList<>();
int[] list=new int[connections.length*2];
for(int[] conn: connections){
list[iList]=conn[0];
if(conn[0]==0)
indexes.add(iList);
iList++;
list[iList]=conn[1];
if(conn[1]==0)
indexes.add(iList);
iList++;
}
//0부터 시작해서 DFS진행
while(!indexes.isEmpty()){
index=indexes.remove();
if(index<0)//이미 처리된 쌍의 나머지 데이터인 경우
continue;
if(index%2==0) {//짝수라면 시작지점
result++;
target_index=index+1;
} else{//홀수라면 도착지점
target_index=index-1;
}
target_val=list[target_index];
list[target_index]=-1;//현재 index와 같이 처리한 쌍의 데이터 무시를 위함
for(i=0; i<list.length; i++)
if(list[i]==target_val)
indexes.add(i);
}
return result;
}
}아래는 GPT에 의해 최적화된 코드이다.
class Solution {
public static int minReorder(int n, int[][] connections) {
int result = 0;
List<List<Integer>> adj = new ArrayList<>(n);
List<List<Integer>> reverseAdj = new ArrayList<>(n);
// 인접 리스트 초기화
for (int i = 0; i < n; i++) {
adj.add(new ArrayList<>());
reverseAdj.add(new ArrayList<>());
}
// 인접 리스트와 역방향 인접 리스트 구성
for (int[] conn : connections) {
adj.get(conn[0]).add(conn[1]);
reverseAdj.get(conn[1]).add(conn[0]);
}
Queue<Integer> queue = new LinkedList<>();
boolean[] visited = new boolean[n];
queue.add(0);
visited[0] = true;
// BFS를 통해 모든 노드 방문
while (!queue.isEmpty()) {
int node = queue.poll();
// 정방향 인접 리스트 탐색
for (int neighbor : adj.get(node)) {
if (!visited[neighbor]) {
result++;
queue.add(neighbor);
visited[neighbor] = true;
}
}
// 역방향 인접 리스트 탐색
for (int neighbor : reverseAdj.get(node)) {
if (!visited[neighbor]) {
queue.add(neighbor);
visited[neighbor] = true;
}
}
}
return result;
}
}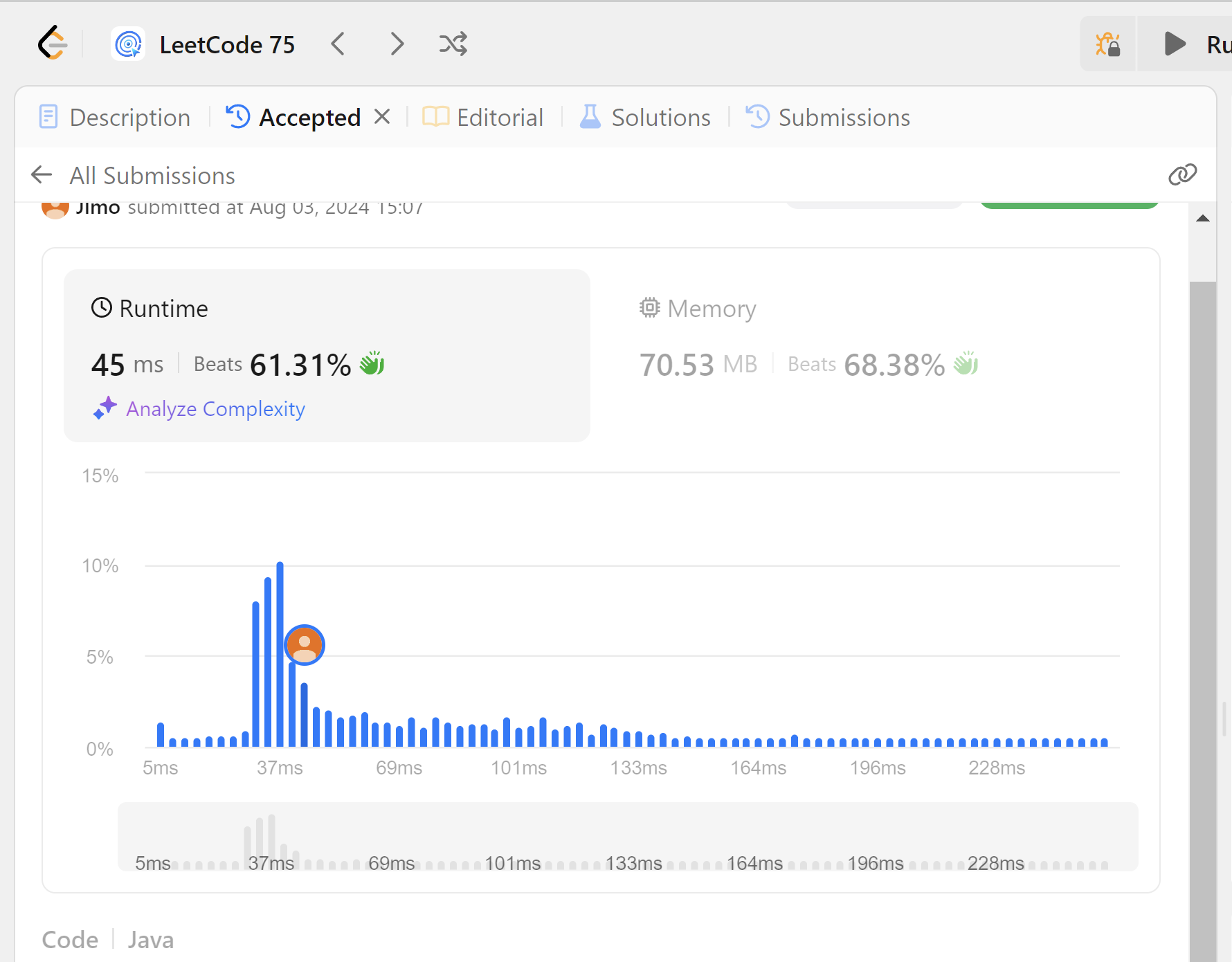
바로 통과해버렸다.
라인 단위로 코드를 분석해보자. 문제를 다시 정리해보면, int[][] connections에 a->b의 관계가 new int[]{a, b}꼴로 담겨있다. 0부터 모든 노드에 다다르기까지 변경해야하는 최소 방향 수를 구해내는 것이 문제의 핵심이다.
1. 초기화 부분
int result = 0;
List<List<Integer>> adj = new ArrayList<>(n);
List<List<Integer>> reverseAdj = new ArrayList<>(n);GPT는 변경하는 방향 수를 저장할 정수형 변수 result외에 다른 변수를 선언하지 않았다. 다음으로 관계를 이중 List를 이용해 표현하였는데, 정방향과 역방향을 구분하여 이중 List를 초기화하였다. 이 때 initial capacity는 n으로 n은 인자로 주어지는 connections의 크기를 의미한다.
기존에 나는 int[][]를 사용해 a->b관계를 표현하기도 하고 List를 사용해 짝수 인덱스에 시작점, 홀수 인덱스에 종점을 두어 a->b관계를 표현해보기도 했는데 전자는 Memory Limit Exceeded가, 후자는 Time Limit Exceeded가 발생하였다. GPT는 이를 이중 List를 이용하여 배열의 표현적 장점과 리스트의 공간적 장점 둘 다 얻었다.
2. 인접 리스트 초기화 및 구성
// 인접 리스트 초기화
for (int i = 0; i < n; i++) {
adj.add(new ArrayList<>());
reverseAdj.add(new ArrayList<>());
}
// 인접 리스트와 역방향 인접 리스트 구성
for (int[] conn : connections) {
adj.get(conn[0]).add(conn[1]);
reverseAdj.get(conn[1]).add(conn[0]);
}노드 개수만큼 원소로 list를 초기화하여 사용 준비를 마친다. 이후 connections를 읽어들이면서 정방향 관계 리스트에 conn을 집어넣고, 역방향에는 conn순서를 뒤집어서 집어넣는다.
3. BFS를 위한 초기화
Queue<Integer> queue = new LinkedList<>();
boolean[] visited = new boolean[n];
queue.add(0);
visited[0] = true;GPT역시 queue를 사용하여 DFS를 수행한다. 다만 visited리스트를 사용하여 방문여부를 표시하며, 최초의 queue값으로 도시의 노드 0을 넣는다. 기존에 나는 관계 기반의 DFS를 수행했다면, GPT는 노드 기반의 DFS를 수행하려는 듯 하다.
4. DFS 수행
// BFS를 통해 모든 노드 방문
while (!queue.isEmpty()) {
int node = queue.poll();
// 정방향 인접 리스트 탐색
for (int neighbor : adj.get(node)) {
if (!visited[neighbor]) {
result++;
queue.add(neighbor);
visited[neighbor] = true;
}
}
// 역방향 인접 리스트 탐색
for (int neighbor : reverseAdj.get(node)) {
if (!visited[neighbor]) {
queue.add(neighbor);
visited[neighbor] = true;
}
}
}
return result;queue에서 값을 얻어오기위해 .remove가 아닌 .poll을 사용하였는데, 차이점으로 .poll은 queue가 비어있을 시 null을 반환한다. 다음으로 정방향 인접 리스트에서 노드 0을(정확히는 node값을)을 출발지로 갖는 노드의 리스트를 찾은 뒤 도착지 노드들을 순회하며, 방문하지 않았다면 result++ 및 queue에 추가하고 방문처리한다. 다음으로 역방향 인접 리스트에서 이웃을 얻어낸 뒤 result++만 제외한 채로 같은 작업을 수행한다.
즉, 정방향 인접 리스트와 역방향 인접 리스트를 나누어 result++를 수행할 조건과 수행하지 않아도 될 조건을 구분한 것이다. 기존의 나는 관계를 int[]에 추가하고 node가 짝수 인덱스면 출발지, 홀수 인덱스면 도착지라는 점을 이용했었다. 이는 내 방식이 더 효율적인 것으로 보인다.
다만 이 방식이 훨씬 효율적인 부분은, 기존의 내 코드는 node값과 연관된 노드들을 찾기 위해 전체 list를 탐색해야했다. 하지만, GPT의 방식은 인접 리스트를 사용하여 전체 list를 탐색할 필요 없이 node에 해당하는 인접 리스트를 전부 queue에 넣으면 되었기에 훨씬 효율적으로 작업이 가능했다. 즉, 내가 GPT를 돌리기 전에 고민했던 이중 for문의 최적화를 생각하기 보다 어떻게 하면 전체 list를 탐색하지 않고 작업을 수행할 수 있을지 고민을 했었다면 이중 인접 list를 생각해냈을지도 모른다. 다만 확신하지 못하는데, 처음에 이 문제를 접하면서 배열도, 리스트로 수행해봤기에 그 중간의 방법인 리스트로 배열처럼 만든다 라는 개념을 생각하기 정말 어려웠다.
두 노드의 방향 관게를 표현하는 방법으로 배열로 표현하는 방법과 배열꼴의 리스트로 표현하는 방법, 인덱스의 홀짝을 이용하여 배열로 표현하는 방법, 정방향과 역방향(애초에 모든걸 꺼꾸로 담는)을 나누어 add하는 방법이 있다는 것을 기억하면 될 듯 하다.
다만 아직 잘 이해가 되지 않는 부분은 왜 굳이 역방향 리스트를 만들었냐인데, 이는 result++의 여부를 구분하기 위한 기능 외엔 특별한 이유가 없어보인다. 만약 GPT의 코드를 조금 더 보완한다면 adj list는 그대로 두고 reverseAdj를 만들지 않고 수행해도 좋은 퍼포먼스가 나오지 않을까 싶다. 이도 수행해보고 싶지만 이 문제에서 피를 너무 빨려 GPT코드리뷰에서 GG를 선언한다.
