[BOJ] 1193_분수 찾기

문제 출처 : https://www.acmicpc.net/problem/1193

문제
무한히 큰 배열에 다음과 같이 분수들이 적혀있다.

1/1 1/2 1/3 1/4 1/5 …
2/1 2/2 2/3 2/4 … …
3/1 3/2 3/3 … … …
4/1 4/2 … … … …
5/1 … … … … …
… … … … … …
이와 같이 나열된 분수들을 1/1 → 1/2 → 2/1 → 3/1 → 2/2 → … 과 같은 지그재그 순서로 차례대로 1번, 2번, 3번, 4번, 5번, … 분수라고 하자.

X가 주어졌을 때, X번째 분수를 구하는 프로그램을 작성하시오.

---

풀이
분수들의 순서에서 규칙성을 찾자!

<순서>
1. 분자/분모 가 나오는 규칙성을 찾는다.
2. 입력 받은 x가 표의 정확히 어느 위치인지 알아야한다.
3. 분자/분모 를 만들자.

1. 분자/분모 가 나오는 규칙성

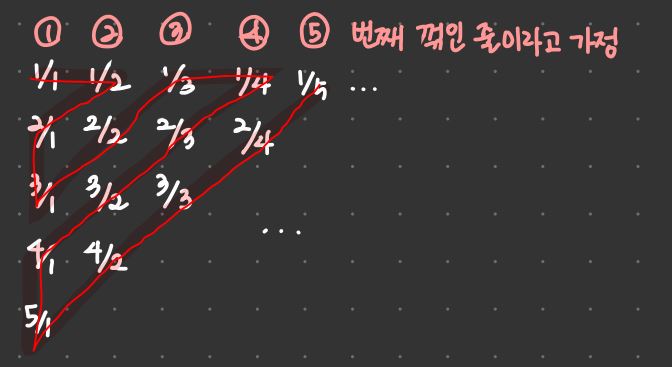나열된 분수를 지그재그로 따라갔을 때, 꺾이는 시점부터 다음 꺾이는 부분 전까지를 한 줄이라고 치고 **줄 번호**를 매기자.

줄 번호 별로 나오는 분수를 나열해보면 규칙이 눈에 쉽게 보인다.

줄 번호가 짝수 일 경우,
분자 : (줄 번호)~1 까지 -1 씩 줄어듬
분모 : 1~(줄 번호) 까지 +1 씩 늘어남

줄 번호가 홀수 일 경우,
짝수일 경우와 반대임을 알 수 있다.

2. 입력 받은 x는 몇 번째 줄에 속해있는가? (x의 줄 번호?)

찾은 규칙성을 토대로 우리는 x번째의 분수를 구하려면 x가 몇 번째 줄 번호 인지 알 필요가 있다.

줄 번호 에 속한 분수의 개수는 줄 번호(개) 만큼 존재한다.

즉, 반복문(while)으로 1(sum)에 다가 +(i) : 1, 2, 3, 4, 5 ... 씩 늘려가면서 더해 각 줄의 첫 번째 숫자를 나타내는 총합(sum)보다 x가 작다면 반복문을 멈춰 줄 번호(i)를 알아낼 수 있다.

int x, sum=1, i=0; //sum은 1 초기화, i는 0 초기화
~~
while(1){
  if(sum>x) break;
  i++;
  sum+=i;
} //i는 줄번호

3. 분자/분모 를 만들자.

위와 같은 과정으로 우리는 x의 줄 번호(i)를 알아냈다.
이제 마지막으로 분자와 분모를 만들어 출력해주면 끝난다.

1번에서 우리는 분자/분모 의 규칙을 찾았다. x번째에 맞는 분수를 만들려면 x번째가 줄 번호 내에서도 몇 번째 수인지 알아야한다. 왜냐하면, (줄번호)~1 까지 1씩 줄어듬. 이라는 규칙에 적용시키려면 (줄번호)-? 몇을 빼줘야 맞는 분자/분모 가 나오는지 알 수 있기 때문이다.
ex) 13은 5번 줄의 3번째이다.

x - 줄 번호의 초항(첫 번째 수) : 줄 번호에서의 x의 위치
ex) 13 - 11 = 2 (초항은 0번째이다, 분자/분모가 (줄번호)-0 이니까!)

sum-i : 줄 번호의 초항
따라서, x-(sum-i) : 줄 번호에서의 x의 위치

sum-i 가 초항인 이유 : 위에서 줄 번호를 구하기 위해 돌린 반복문에서 sum은 x의 값보다 한 줄 앞의 초항으로 만들어진다. 따라서, i(줄 번호)를 빼준 값이 i의 초항과 같아진다.

int num, den; //분자, 분모
~~
if(i%2==0){ //짝수라면
    num=1+(x-(sum-i)); //(sum-i) : 줄번호의 초항(첫번째 수)
    den=i-(x-(sum-i)); //x-(sum-i) : 초항으로부터 x가 얼마나 떨어져있는지 (줄번호)의 몇번째 수 인가!
}
else{ //홀수라면
    num=i-(x-(sum-i));
    den=1+(x-(sum-i));
}

---

풀이 코드

#include<iostream>
using namespace std;

int main(void)
{
    cin.tie(NULL); ios_base::sync_with_stdio(false);

    int num, den; //분자, 분모
    int x,sum=1,i=0;
    cin>>x;

    while(1){
        if(sum>x) break;
        i++;
        sum+=i;
    } //i는 줄번호

    if(i%2==0){ //짝수라면
        num=1+(x-(sum-i)); //(sum-i) : 줄번호의 초항(첫번째 수)
        den=i-(x-(sum-i)); //x-(sum-i) : 초항으로부터 x가 얼마나 떨어져있는지 (줄번호)의 몇번째 수 인가!
    }
    else{ //홀수라면
        num=i-(x-(sum-i));
        den=1+(x-(sum-i));
    }
    cout<<num<<"/"<<den;
}

---

잡담
'기본 수학' 카테고리에 있는 문제들은 문제의 '규칙성'을 찾는 게 핵심 포인트인 문제가 많은 것 같다.