
공간 복잡도 (Space Complexity)
: 알고리즘을 프로그램으로 실행하여 완료하는 데까지 필요한 총 저장공간
예전보다 컴퓨터 성능의 증가로 중요도는 떨어졌다. 최근에는 시간 복잡도를 더 우선시해서 프로그래밍한다.
공간 복잡도 = 고정 공간 + 가변 공간 으로,
고정 공간 이란 말그대로 고정적인 저장 공간으로 '프로그램 저장 공간', '변수 및 상수를 저장하는 공간' 이다.
가변 공간 이란 실행 과정에서 사용하는 자료와 변수의 공간과 함수 실행 정보를 저장하는 공간이다.
시간 복잡도 (Time Complexity)
: 알고리즘을 프로그램으로 실행해 완료하는 데까지 소요되는 시간
프로그램에 얼마만큼의 실행 단계(step)가 있는가? 라고 생각하면 쉽다. 당연히, 단계가 적을수록 좋다.
시간 복잡도 = 컴파일 시간 + 실행 시간 이지만,
컴파일 시간은 시간복잡도에서 유의미하지 않다.
실행 시간은 정확한 실행 시간을 측정하기보다는 실행 빈도수를 구하여 사용한다.
(why? 같은 프로그램도 컴퓨터 성능에 따라 시간이 달리 측정되기 때문에 '정확한 시간'은 의미X)
알고리즘 성능 분석 표기법
- 빅-오 표기법 O(f(n))
- 빅-오메가 표기법 Ω(f(n))
- 빅-세타 표기법 θ(f(n))
f(n) = O(g(n)) 으로 표현하는 것은 f(n) ≤ O(g(n)) 함수 f의 증가속도가 g보다 빠르지 않다.
f(n) = Ω(g(n)) 으로 표현하는 것은 f(n) ≥ Ω(g(n)) 함수 f의 증가속도가 g보다 느리지 않다.
f(n) = Θ(g(n)) 으로 표현하는 것은 f(n) = θ(g(n)) 함수 f의 증가속도가 g랑 비슷하다.
- 세 가지 표기법 모두 집합으로 정의된다. 2n+3
=O(n)의 경우 2n+3∊O(n)으로 쓰는 것이 맞지만 보통=으로 쓴다.
따라서,=은∊의 대신이므로 O(n)=2n 과 같이 방정식을 오른편에 위치하도록 쓰면 안된다.
빅-오 표기법 O(f(n))
: 함수의 상한을 나타내기 위한 표기법. 최악의 경우에도 f(n)의 수행 시간 안에는 알고리즘 수행이 완료된다는 것을 보장한다
=> O(f(n))은 점근적 증가율이 f(n)을 넘지 않는 모든 함수의 집합 = 최고차항의 차수가 f(n)과 일치하거나 더 작은 함수의 집합
ex) n², 2n²+5, 6n+3, 2nlogn+3n, 300 등
표현방법
1. 실행빈도수를 구해 실행 시간 함수를 찾고
2. 이 함수값에 가장 큰 영향을 주는 n에 대한 항을 한 개 선택해 계수는 생략하고
3. O의 오른쪽 괄호()안에 표시
ex) 실행시간 함수 4n+2의 가장 영향이 큰 항은 4n, 여기서 계수 4생략하면 시간 복잡도 O(n) 이 된다.
- [ 수학적 정의 ]
θ(g(n)) = { f(n) | ∃c>0, n0>=0 s.t.∀n>=n0, cg(n) >= f(n)
n에 관한 두 함수 f와 g가 정의될 때, 충분히 큰 모든 n에 대하여 (n>=n0) cg(n)을 항상 f(n)보다 크거나 같게 만드는 상수 c가 존재하면, 이때 f(n)을 O(g(n))이라 표기한다.
빅-오메가 표기법 Ω(f(n))
: 함수의 하한을 나타내기 위한 표기법. 어떤 알고리즘의 시간 복잡도가 Ω(f(n))이라면 알고리즘 수행에는 적어도 f(n)의 수행 시간이 필요함을 의미
=> Ω(f(n))은 점근적 증가율이 적어도 f(n)이 되는 모든 함수의 집합 = 최고차항의 차수가 f(n)과 일치하거나 더 큰 함수의 집합
ex) n², 2n²+5, n²+√n, n³, n²logn+1 등
- [ 수학적 정의 ]
θ(g(n)) = { f(n) | ∃c>0, n0>=0 s.t.∀n>=n0, cg(n) <= f(n)
n에 관한 두 함수 f와 g가 정의될 때, 충분히 큰 모든 n에 대하여 (n>=n0) cg(n)을 항상 f(n)보다 작거나 같게 만드는 상수 c가 존재하면, 이때 f(n)을 Ω(g(n))이라 표기한다.
빅-세타 표기법 θ(f(n))
: 상한과 하한이 같은 정확한 차수를 표현하기 위한 표기법
=> θ(f(n))은 점근적 증가율이 f(n)과 일치하는 모든 집합 = 최고차항의 차수가 f(n)과 일치하는 함수의 집합
ex) n², 2n²+5, n²+√n 등
- [ 수학적 정의 ]
θ(g(n)) = O(g(n)) ∩ Ω(g(n))
즉, θ(f(n))는 O(f(n))과 Ω(f(n)) 모두에 속하는 함수의 집합
=> 일반적으로 최악의 경우를 고려한 해결책을 찾기 때문에 빅-오 표기법을 주로 사용
알고리즘에 따라 상수, logn, n, nlogn, n^2, n^3, 2^n 등의 실행 시간 함수가 있다.
n값이 커질 수록 실행 시간 함수값의 크기는 O(1) < O(log n) < O(nlog n) < O(n²) < O(2ⁿ) 순으로 커진다.
실행 빈도수가 상수값이라면 O(1)로 표기한다. 가장 빠른 실행 시간 함수다.
빅-오 표기법 O(f(n))
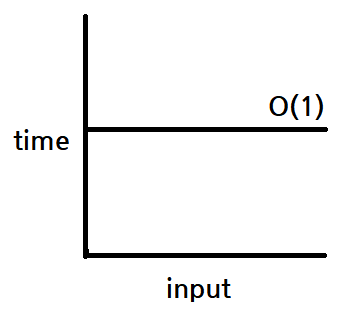
O(1) - Constant : 상수
입력값이 증가해도 언제나 일정한 시간이 걸리는 알고리즘.
void print1(arr){
printf(arr[0]);
}arr 배열의 크기가 얼마든 수행하는 단계(step)는 1로 동일하다.
void print2(arr){
printf(arr[0]);
printf(arr[0]);
}print를 2번 하더라도 O(2) 가 아닌 O(1)로 표기한다. 시간 복잡도에서 상수는 유의미한 영향력을 가지지 않는다.
O(log2 n) - Logarithmic
: 입력 데이터의 크기가 커질수록 처리 시간이 log만큼 짧아지는 알고리즘.
대표적 예시인 이진트리의 경우 노드를 이동할 때마다 경우의 수가 절반으로 줄어든다.
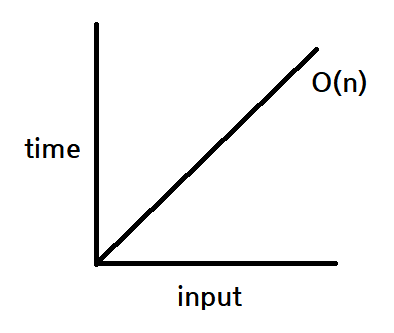
O(n) - Linear : 선형
: 입력값이 증가함에 따라 시간 역시 선형적으로 같은 비율로 증가하는 알고리즘.
예시 1)
void printNum(n){
for(int i=0; i<n; i++){
//n만큼 반복
}
}n이 증가할 때마다 실행시간이 역시 똑같이 증가하는 선형 방식.
예시 2)
void printNum2(n){
for(int i=0; i<2n; i++){
//2n만큼 반복
}
}예시 2) 의 경우 1) 보다 두배 그러니까, n이 1씩 늘어날 경우 2초씩 증가한다고 볼 수 있지만, O(2n) 이 아니라 O(n) 으로 표기한다.
왜냐하면, 입력값이 커질수록 계수가 가지는 영향력은 작아지기 때문에 O(n)으로 통일하는 것이다.
O(n²) - Qudratic
: 입력값이 증가함에 따라 시간이 n의 제곱수 비율로 증가
ex) 입력값이 1일 경우 1초가 걸리던 알고리즘이 5를 넣었더니 25초가 걸리는 경우.
void Qudratic(n){
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
}
}
}O(2ⁿ) - Exponential
: 빅오 중 가장 느린 시간 복잡도
제일 느리기 때문에 구현한 알고리즘의 시간 복잡도가 O(2n)이라면 다른 접근 방식을 고민해 보는 것이 좋다.
ex) 피보나치 수열
int fibonacci(n){
if(n<=1){
return 1;
}
return fibonacci(n-1) + fibonacci(n-2);
}