📍 출처
출처 : https://www.acmicpc.net/problem/11729
📝 문제
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로 옮기려 한다.
- 한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다.
- 쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.
이 작업을 수행하는데 필요한 이동 순서를 출력하는 프로그램을 작성하라. 단, 이동 횟수는 최소가 되어야 한다.
아래 그림은 원판이 5개인 경우의 예시이다.

⌨️ 입력
첫째 줄에 첫 번째 장대에 쌓인 원판의 개수 N (1 ≤ N ≤ 20)이 주어진다.
🖨 출력
첫째 줄에 옮긴 횟수 K를 출력한다.
두 번째 줄부터 수행 과정을 출력한다. 두 번째 줄부터 K개의 줄에 걸쳐 두 정수 A B를 빈칸을 사이에 두고 출력하는데, 이는 A번째 탑의 가장 위에 있는 원판을 B번째 탑의 가장 위로 옮긴다는 뜻이다.
⌨️ 예제 입력
3
🖨 예제 출력
7
1 3
1 2
3 2
1 3
2 1
2 3
1 3
📚 내가 제출한 코드
import java.util.Scanner;
public class App {
public static StringBuilder sb = new StringBuilder();
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int num = sc.nextInt();
sb.append((int)(Math.pow(2, num) - 1) + "\n");
hanoi(num,1,2,3);
System.out.print(sb);
}
public static void hanoi(int n, int start,int mid, int to){
if(n==1){
sb.append(start + " " + to + "\n");
return;
}
hanoi(n-1, start, to, mid);
sb.append(start + " " + to + "\n");
hanoi(n-1, mid, start, to);
}
}
✏️ 내가 제출한 코드에 대한 설명
[하노이 탑의 재귀적 원리]
1. n개의 고리가 하노이의 탑에 꽂혀있다고 가정해보자
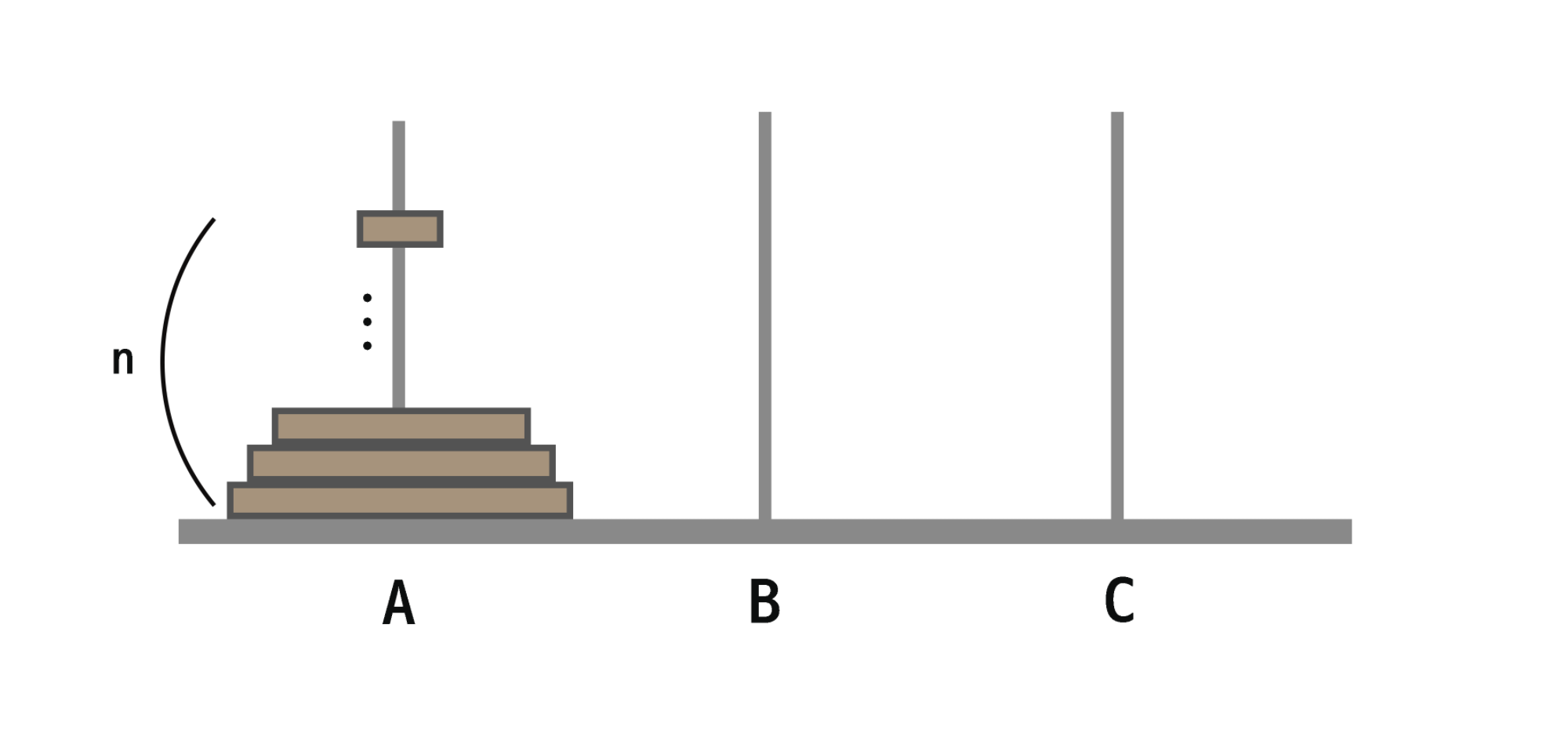
2. 가장 큰 고리가 A-C로 가기 위해선 n-1개의 고리가 A-B로 이동하는 것이 선행되어야 한다.
물론 n-1 번만큼 B 로 이동하기 위한 같은 반복을 할 것이다.
즉 A 에서 B로 가는 것을 Hanoi 함수라고 한다면, n-1 개만큼 반복한다는 의미다.
즉, 이동 횟수는 Hanoi(n-1) 이다.
즉, 아래 그림과 같이 된다.
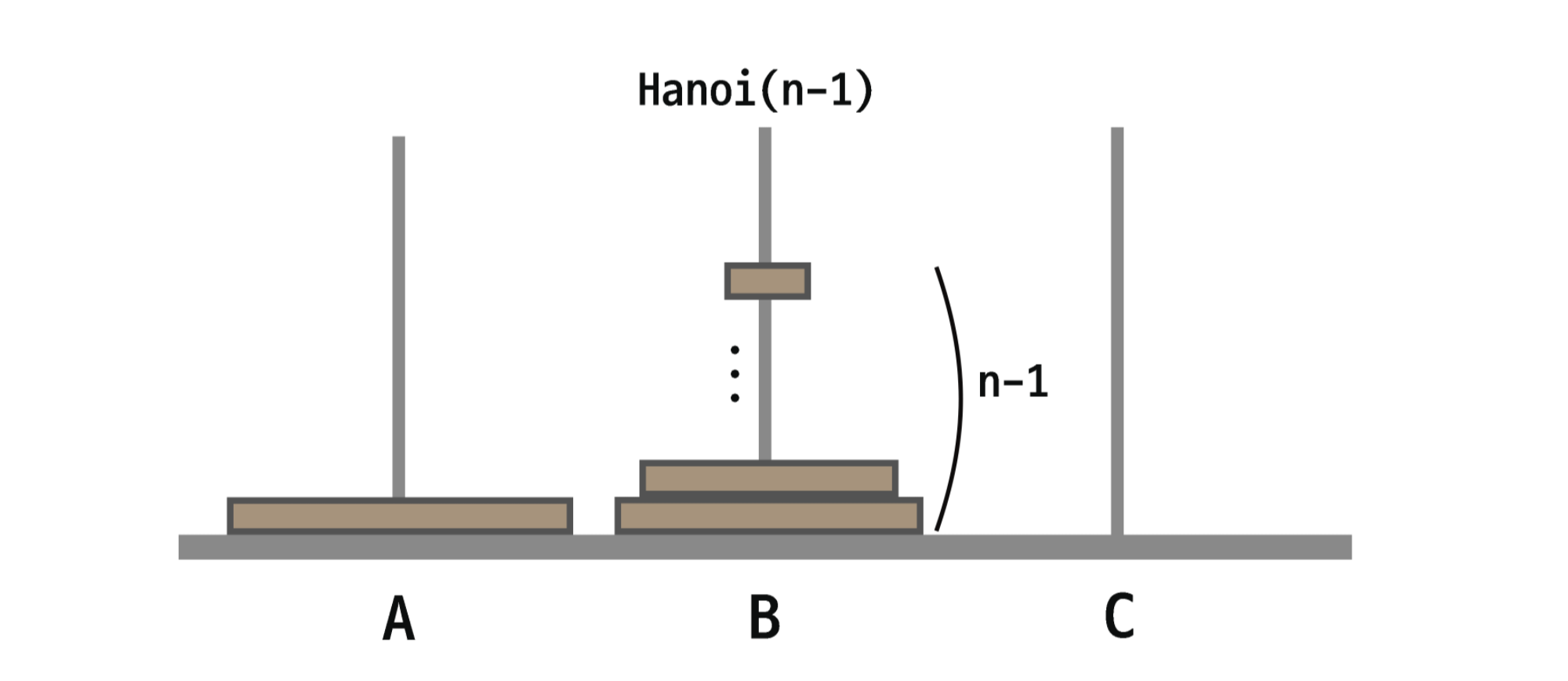
-
그리고 A에 있는 가장 큰 원판을 A에서 C로 이동한다.
이때의 이동횟수는 1회가 된다.
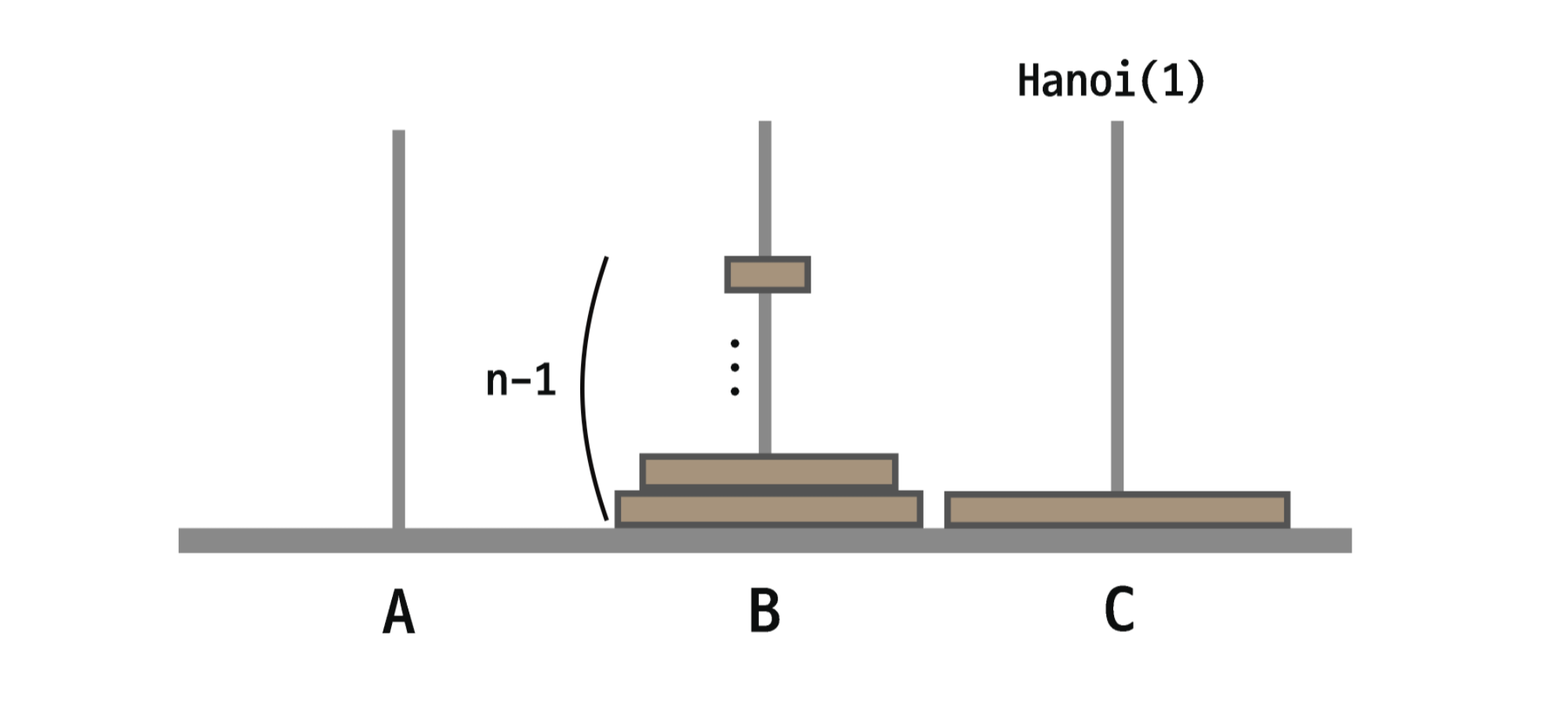
-
앞서 n-1개의 원판을 A에서 B에서 이동했던 것처럼 이번엔 n-1개의 원판을 B에서 C로 이동해준다. 횟수는 첫 번째와 같이 Hanoi(n-1)이 된다.
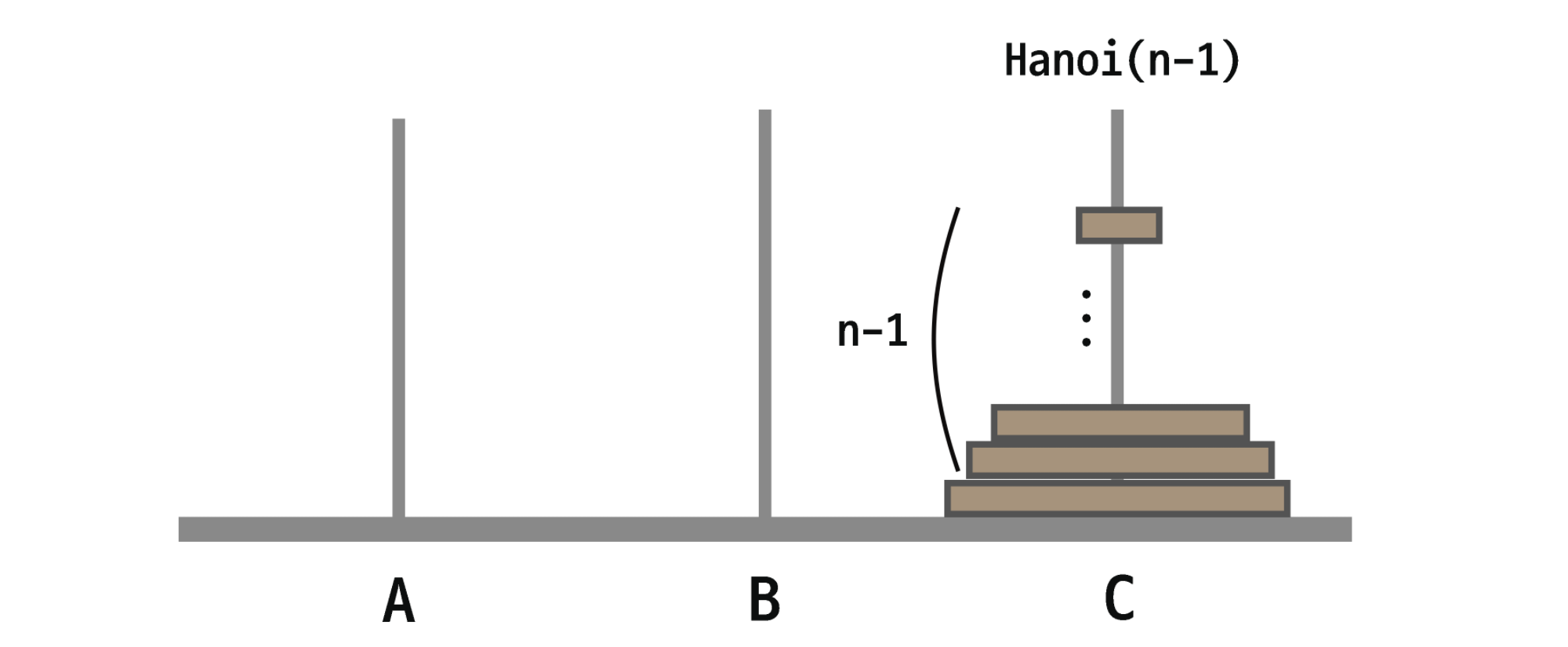
어떤식으로 재귀를 하면 되는지 알아봤으니 이제 첫 번째 줄에 출력해야하는 K를 구해보자. 아래는 원판의 갯수에 따른 이동횟수이다.
원판 1 , 횟수 1
원판 2 , 횟수 3
원판 3 , 횟수 7
원판 4, 횟수 15
원판 5, 횟수 31
원판 n, 횟수 2의n승 - 1
이제 규칙이 보일것이다.
규칙으로는 2의 n승을 한뒤 -1을 해주는 것이다.
이것으로 첫 번째 줄에 출력해야하는 원판의 이동횟수는 구하였다.
사실 앞의 내용을 이해하였다면 문제의 90%를 풀었다해도 과언이 아니다.
일단 재귀를 통해 가장 작은 단위로 들어간다.
즉, 먼저
A 에서 B 로 원판을 이동하는 경우의
A 에서 B 로 원판을 이동하는 경우의
A 에서 B 로 원판을 이동하는 경우의
...이렇게 계속 A 에서 B로 이동하는 함수를 재귀호출하여 이동해야 할 원판이 1개가 되면 그 때 A 에서 B로 이동했다는 것을 출력한 뒤, 함수를 리턴하면 된다.
그렇게 원판이 1개일 때 A 에서 B로 이동한 함수가 닫히면
그 전 단계 재귀로 다시 돌아오면 원판이 2개일 때가 된다. 이때는 앞서 그림에서 봤듯이 1개의 원판이 A 에서 C로 이동하면 되므로, 이 때의 경우를 출력한다.
출력이 끝나면, B 에서 C 로 이동하도록 다시 재귀호출을 한다.
이 메커니즘을 그대로 반영하면 된다.

