201216 개발일지(9일차) - 파이썬 재귀함수(팩토리얼, 하노이 탑, Z모양 탐색)

재귀함수(Recursive Function)란?

어떤 함수에서 자기 자신을 다시 호출하여 작업을 사용하는 함수(알고리즘)

(지애가 좋아하는 대사가 여기서 쓰일 줄이야..)

개념은 대략적으로 이해했는데, 적용과 응용이 힘들다.

완벽히 이해하지 못해서 그런 것이라고 생각한다. 재귀함수를 이용해서 순서대로 아래 3개 문제를 풀어볼 텐데, 완벽히 이해하고 넘어가자.
  ※ 재귀함수는 반복문으로 다 나타낼 수 있지만 재귀 개념을 활용해야 단순해지는 경우가 있으니 개념을 꼭 확실히 하자.

재귀함수 개념 요약 ( Ex : Func(n)이 재귀함 수 일 때)

• 종료조건을 먼저 붙여줘야 한다. (주로 n==0 혹은 n==1일 때)
• 관계식 혹은 관계 흐름을 만들어줘야 한다.
  예를 들어, 팩토리얼 관계식은 Func(n) = n * Func(n-1) 이다.

1. 팩토리얼(백준 10872번) : 내 벨로그 201212 개발일지에도 풀었으나, 개념의 이해를 돕기 위해 짚고 넘어가자.
2. 하노이 탑(백준 1914번) : 개념은 너무 쉽게 이해되지만 적용하는 데 어려움이 있다. 하노이 탑을 이해하면서 재귀함수 개념을 완벽히 익히자.
3. Z(백준 1074번) : 개념을 완벽히 이해했으면 응용하는 데 이 문제를 풀어보자. 여기까지 완벽히 하면... 오늘 편히 잘 수 있다. ⇩
   

1. 팩토리얼(!)문제 : 팩토리얼이란 1부터 본인까지의 자연수를 곱한 값이다.
   따라서, 반복문을 통해 간단히 풀 수도 있지만 재귀함수 개념을 활용할 것이다.
   1-1) 종료조건을 붙여준다. (1!) = 1을 알기 때문에 Func(1)=1 이라는 것을 표현해주는 것이다.
   1-2) return값 Func(n) = n * Func(n-1)을 잘 입력해준다. (관계식 or 관계흐름 만들기)
   

def Func(n):
    if n==1 :		#종료조건 만드는 것이 중요하다.
        return 1
    else :
        return n * Func(n-1)

2. 하노이 탑 문제 : 아래 그림을 보고, 귀납적 추론에 대해 생각하면서 머리를 쓰면 이해에 도움이 될 것이다. Ex) 1번 도미노가 쓰러지면, 2번 도미노가 쓰러진다. n번 도미노가 쓰러지면, n+1번 도미노가 쓰러진다 → 모든 도미노가 쓰러진다.
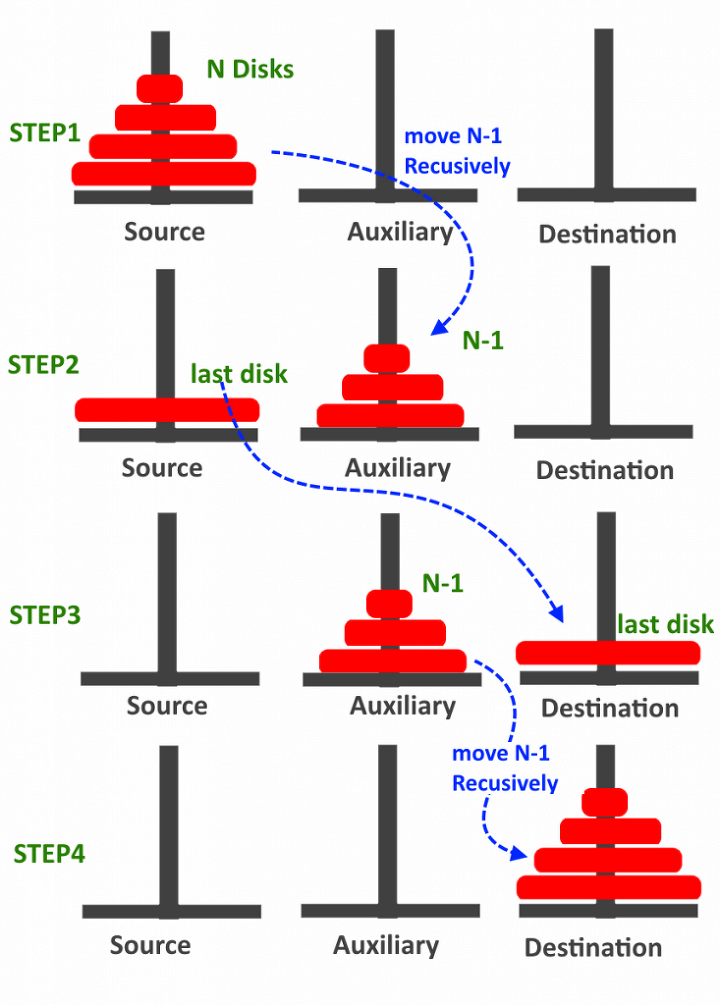
   2-0) n개의 탑을 출발지(1번 기둥, from)에서 목적지(3번 기둥, to)으로 이동시킨다. 이를 위해 위의 그림처럼 생각하면 된다.
   2-1) 종료조건을 붙여준다. 탑이 1개라면, 1번 기둥에서 3번으로 옮겨주면 끝!
   2-2) 관계 흐름을 생각해야 하는데, 아래 코드 주석에 자세히 적었다.

def Func(n, fr, to):
    if n==1 :				#종료조건
        return print(fr, to)		#fr=출발지(1번 기둥) / to=목적지(3번 기둥)
    else :
        Func(n-1, fr, 1+2+3-fr-to)      #위의 그림의 STEP2 단계로, n-1개의 탑을 출발지(1번 기둥)도 목적지(3번 기둥)도 아닌 중간지(2번 기둥)으로 이동한다.
        print(fr, to) 			#위의 그림의 STEP3 단계로, 가장 큰 탑을 출발지(1번 기둥)에서 목적지(3번 기둥)로 이동한다.
        Func(n-1, 1+2+3-fr-to, to)	#위의 그림의 STEP4 단계로, n-1개의 탑을 중간지(2번 기둥)에서 목적지(3번 기둥)로 이동한다.

여기까지 잘 따라왔다면 재귀함수에 대해 어느정도 이해는 완료한 것이다! 라고 감히 말해봅니다..

         3. Z모양 탐색 : 2ⁿ x 2ⁿ 배열을 아래 그림처럼 탐색할 때, 탐색 순서를 숫자로 표시한 것이다. n이 주어졌을 때, r행 c열을 몇 번째로 탐색하는 지 출력해야 한다.

아래 그림 참고

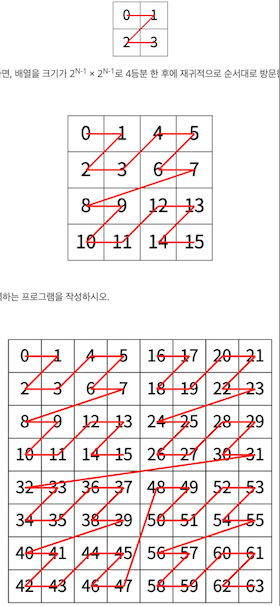
        3-0) 좌상단, 우상단, 좌하단, 우하단 순으로 숫자가 커짐에 유의하여 생각한다.
        3-1) 종료조건은 n==0일 때, 즉 1 x 1 배열에서 끝내면 된다. (종료조건 n==1일 때, 즉 2 x 2 배열에서도 끝내기 가능!)
        3-2) 관계식을 4가지(좌상단, 우상단, 좌하단, 우하단)로 나누어 생각해야 한다

# n==0일 때로 푼 것

def Zman(n, r, c):
    half=2**(n-1)						#half는 사각형의 절반 위치
    result=0							#초기값(0,0)을 0으로 지정
    if n==0:							#n이 0 일 때 풀기
        return result
    elif r<half and c<half :					#알고싶은 값이 좌상단에 위치할 때
        result= Zman(n-1,r,c)					#n-1만 해주고, r과 c는 그대로
    elif r<half and c>=half :					#알고싶은 값이 우상단에 위치할 때
        result= 4**(n-1) + Zman(n-1,r,c-half)			#n-1해주고, c도 half만큼 뺌 + 4**(n-1)만큼 더해줌
    elif r>=half and c<half :					#알고싶은 값이 좌하단에 위치할 때
        result= 2*4**(n-1) + Zman(n-1,r-half,c)			#n-1해주고, r을 half만큼 뺌 + 2*4**(n-1)만큼 더해줌
    elif r>=half and c>=half :					#알고싶은 값이 우하단에 위치할 때
        result= 3*4**(n-1) + Zman(n-1,r-half,c-half)		#n-1해주고, r과 c 모두 half만큼 뺌  + 3*4**(n-1)만큼 더해줌
    return result

        아래 코드는 종료조건을 n==1로 할 때, 푼 것이다.

def Zman(n, r, c):
    half=2**(n-1)
    result=0
    if n==1:
        if r==0 and c==0:
            return result
        if r==0 and c==1:
            return result + 1
        if r==1 and c==0:
            return result + 2
        if r==1 and c==1:
            return result + 3
    elif r<half and c<half :
        result= Zman(n-1,r,c)
    elif r<half and c>=half :
        result= 4**(n-1) + Zman(n-1,r,c-half)
    elif r>=half and c<half :
        result= 2*4**(n-1) + Zman(n-1,r-half,c)
    elif r>=half and c>=half :
        result= 3*4**(n-1) + Zman(n-1,r-half,c-half)
    return result

오늘의 공부 후기 :
    오늘 재귀함수에 대해 집중 공부했다.. 어제는 정말 너무 이해가 안돼서 절망 수준이었는데, 계속 보고 노력하니까 신기하게 이해가 됐다. 이제 하노이 탑 같은 내용까지는 확실히 활용할 수 있다. 그래서 2번까지 풀고 굉장한 자신감을 얻었는데, 3번을 풀다가 또 좌절해버렸다.. 그래도 포기하지 않고 해결해냈으니 뿌듯하다.
    무의식은 진짜인지 가짜인지 잘 구분하지 못한다고 한다. 내가 진짜 잘하고 있다고 계속 되뇌어주고, 똑똑하다고 계속 말해줘야겠다. 주변에 잘하는 분들이 많아서 자꾸 의기소침해지고 불안감이 드는데, 그건 당연히 그 분들이 내가 공부하기 이전에 많은 시간과 에너지를 쏟았기 때문임을 안다. 불안해하지말고 차근차근 정상을 향해 걸어가자. 꾸준히.