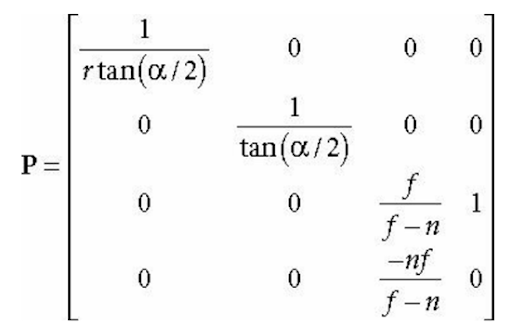Projection, screen 변환

view space => (clip, projection) space

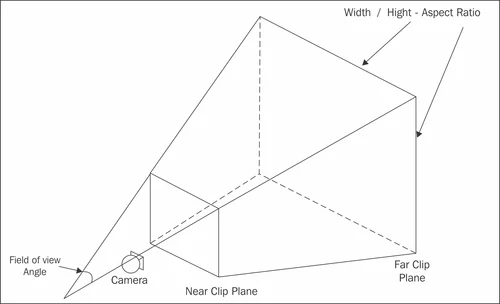
이미지 출처

카메라로부터 z축으로 1만큼 떨어지고 원점 (0,0)에서 상하좌우 크기가 1인 평면으로 투영

(x, y, z ,1)

=>

원근 투영

z 축값에 따라 비율이 달라짐

$\left( \frac{x}{z},\ \frac{y}{z},\ z, \ w \right)$

---

해상도 처리

윈도우의 width와 height 비율이 다름

=>

window width, height

$r = \frac{width}{height}$

=>

$\left( \frac{x}{rz},\ \frac{y}{z},\ z, \ w \right)$

---

카메라 각도 처리

각도인 Fov $\theta$값 따라 1:1:1 비율이었던 직각삼각형 opposite의 크기가 달라짐

=>

opposite의 크기 = $tan(0.5 \theta)$

=>

모든 값들을 크기 만큼 나누어 강제로 최대값을 1로 만듬

$\left( \frac{x}{rztan(0.5 \theta)},\ \frac{y}{ztan(0.5 \theta)} ,\ z, \ w \right)$

---

해당 식을 행렬로 만들 수 없음 => 선형성 x

1. z축 값을 나중에 나누도록 함 (rasterizer 단계에서 실행 된다.)

2. z축 값은 0 ~ 1값인 비율로 나타내야 함

=>

z값은 선형
사용하지 않는 w 값을 z 저장용도로 사용

z축 값은 최대일 때 1, 최소일 때 0

y(z) = az + b
y(near) = an + b = 0
y(far) = af + b = 1

$a = \frac{f}{f-n}$
$b = \frac{-nf}{f-n}$

=>

$\left( \frac{x}{rtan(0.5 \theta)},\ \frac{y}{tan(0.5 \theta)} ,\ \frac{f(z-n)}{f-n}, \ z \right)$

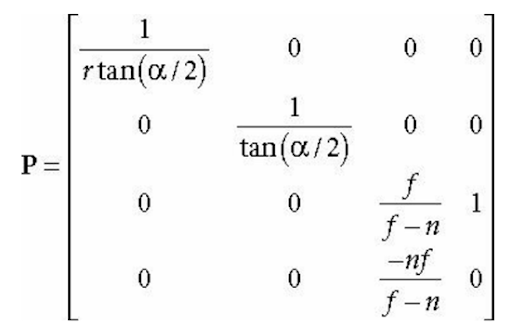
이미지 출처

---

projection space => (view port, window, screen) space

NDC 좌표계에서 실제 화면(screen) 좌표로 변환

NDC에서 모니터 안의 맵핑되는 윈도우를 viewport라고 함

NDC에서의 비율과 viewport에서의 비율이 같아야 한다는 것을 이용

모니터 좌표계는

좌측 상단 (0,0)

우측 하단 (모니터 해상도 width, 모니터 해상도 height)

left = viewport의 해상도 x 좌표
top = virwport의 해상도 y 좌표
W = viewport의 width
H = viewport의 hegith

$X = left + W \times \left( \frac{x+1}{2} \right)$
$Y = top + H \times \left( \frac{y-1}{2} \right)$

$S=\left[ \begin{matrix} 0.5W&0&0&0 \\ 0&-0.5H&0&0 \\ 0&0&MaxDepth - MinDepth&0 \\ Left + 0.5W & Top+0.5H & MinDepth & 1\end{matrix} \right]$

viewport에서도 여러 개의 view를 그리기 위해 depth를 사용할 수 있음 (활용할 일이 많지 않다고 함)

z 값 0에서 1의 값들을 함수 f(z) =(max - min)z + min로 나타냄