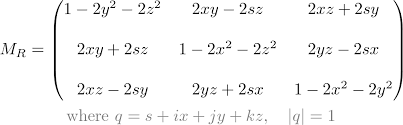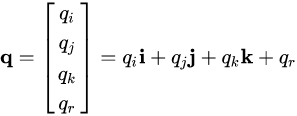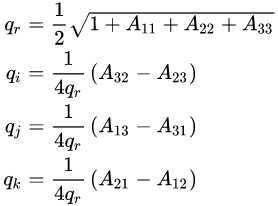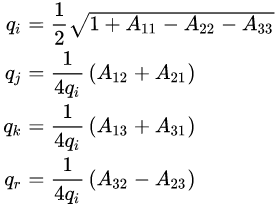Quaternion

오일러 각의 회전에 문제가 있음 => 짐벌락 현상

유니티 엔진에서는 z축, x축, y축 순으로 회전을 계산함

z축의 회전에 따라 x,y 축이 영향을 받고 x축에 따라 y축이 영향을 받음

문제는 2번째 계산되는 축이 회전했을 때 1, 3번째 축이 겹치면서 발생

=>

2개의 회전축이 같아지면서 축이 하나 소실되어 회전이 자유롭게 되지 못함

---

복소수

z = a + bi
a: 실수부
bi: 허수부
i: 허수 단위

이미지 출처

$|z| = |a+bi| = \sqrt{a^2+b^2}$
켤레 복소수 $z^* = a-bi$
$z \times z^* = a^2+b^2 = |z|^2$

복소 평면
x축에는 실수부를 표현, y축은 허수부를 표현

이미지 출처

$Z_1 = r_1(cos\theta_1+isin\theta_1)$
$Z_2 = r_2(cos\theta_2+isin\theta_2)$
$Z_1 \times Z_2 \\= r_1r_2((cos\theta_1cos\theta_2 - sin\theta_1sin\theta_2) + i(sin\theta_1cos\theta_2 + cos\theta_1sin\theta_2) )$
$= r_1r_2(cos(\theta_1 + \theta_2) + isin(\theta_1 + \theta_2))$

$Z_1$을 벡터라고 생각하고 $Z_2$의 크기가 1인 경우 단위 복소수일 경우

$Z_1$을 회전시키는데 사용할 수 있음

---

복소수의 행렬 표현

$a+bi = \left[ \begin{matrix} a & -b \\ b & a \end{matrix} \right]$

실수부 단위 행렬 $E = \left[ \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} \right]$

허수부 단위 행렬 $I = \left[ \begin{matrix} 0 & -1 \\ 1 & 0 \end{matrix} \right]$

$I^2 = -E$

$r(cos\theta+isin\theta) = r\left[ \begin{matrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{matrix} \right]$

= 2차원 회전 행렬

---

Vec4 (x,y,z,w)

q = xi + yj + zk + w = ($\vec{v}, s$)

xi + yj + zk: 벡터부

w: 스칼라부 실수부

$i^2 = j^2 = k^2 = -1$

$i->j->k$
$ij = k, ji = -k \\jk=i, kj=-i \\ki = j, ik = -j$

$q^* = (-\vec{v}, s)$
$|q| = \sqrt{qq^2} = \sqrt{|\vec{v}|^2 + s^2} = \sqrt{x^2+y^2+z^2+w^2}$

$q^{-1} = \frac{1}{q} \cdot \frac{q^*}{q^*}=\frac{-\vec{v} + s}{|\vec{v}|^2 + s^2}$
$|q|=1$이라면 $q^{-1} =q^*$

$(q_1q_2)^* = q_2^*q_1^*$

$q_1q_2 = (\vec{v_1} \times \vec{v_2} + s_1\vec{v_2} + s_2\vec{v_1},\ s_1s_2-\vec{v_1} \cdot \vec{v_2}) = (\vec{v}, s)$

실수부가 0인 쿼터니언: pure quaternion

---

$\vec{v}$를 $\vec{a}$ 방향으로 $\theta$만큼 회전 시킨 벡터
$q = (sin{\frac{\theta}{2}}\vec{a}, cos{\frac{\theta}{2}}),\ |q| = 1$
$V' = qvq^*$

연속 회전 $q_1$회전 후 $q_1$회전

$q_2(q_1\vec{v}q^*_1)q^*_2\\ = (q_2q_1)\vec{v}(q^*_1q^*_2) \\ = (q_2q_1)\vec{v}(q_2q_1)^*$

연속 회전 시 $q_2q_1$과 $(q_2q_1)^*$을 미리 구해놓을 수 있음

---

쿼터니언을 행렬로 변환

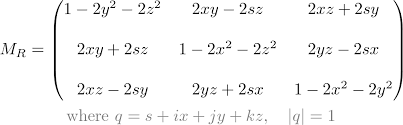
이미지 출처

q일때와 -q일때가 동일

---

행렬을 쿼터니언으로 변환

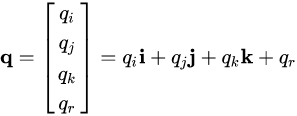
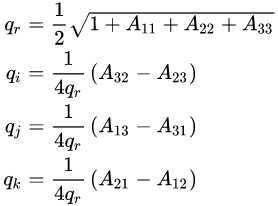
$q_r$이 0이거나 매우 작아질수록 오차가 매우 커짐

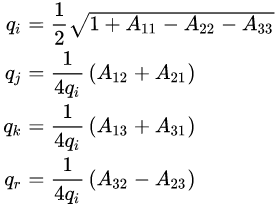
$q_i, q_j, q_k$ 중에 가장 큰 값을 찾아 해당 값을 나누는 공식으로 사용하게 됨

위 공식은 $q_i$가 가장 큰 값인 경우

이미지들 출처