[BOJ] 21736 - 헌내기는 친구가 필요해 (Java)

알고리즘

• 그래프 이론
• 그래프 탐색
• 너비 우선 탐색
• 깊이 우선 탐색

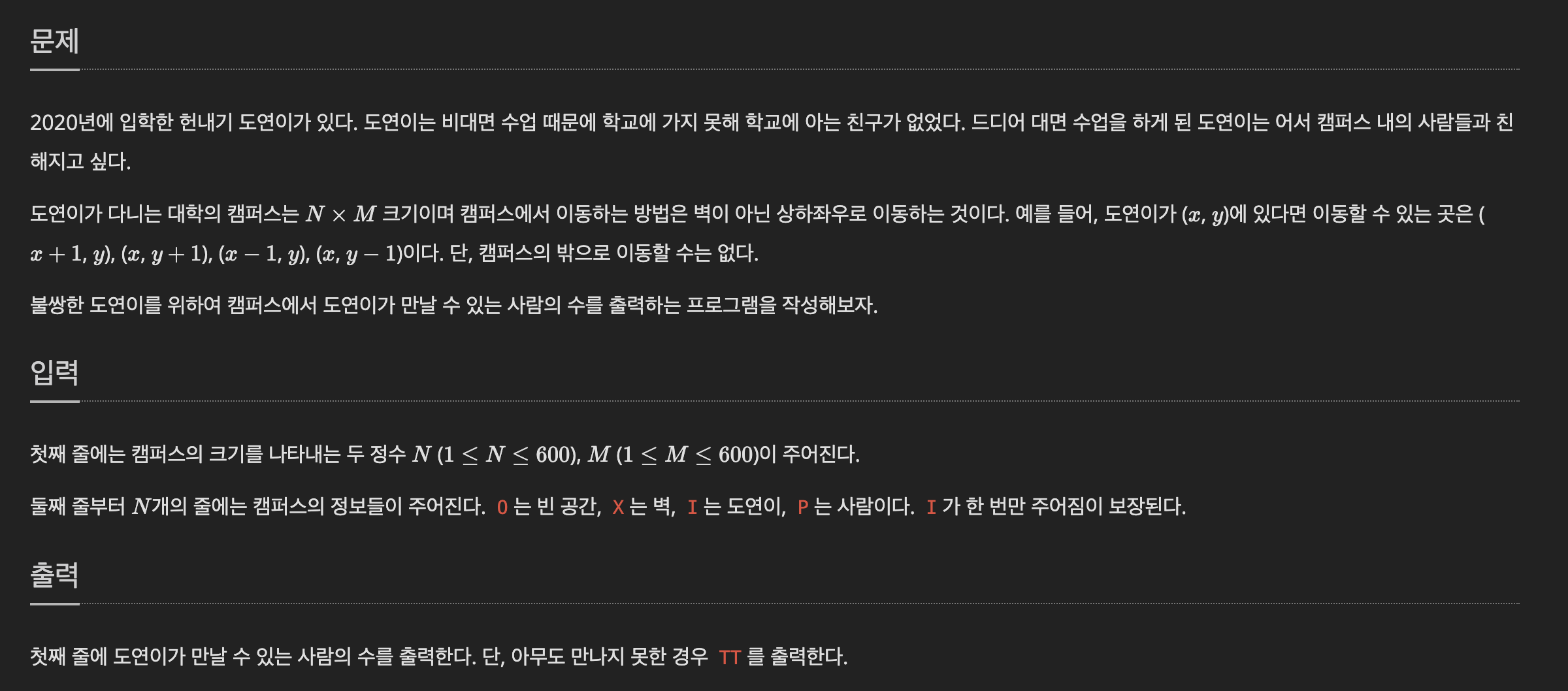
1. 문제

• 캠퍼스에서 도연이(I)의 위치에서 시작하여 상하좌우로 이동하면서 주변에 있는 친구들(P)을 찾아 몇 명의 친구들을 만날 수 있는지 확인하는 문제

2. Idea

• DFS(깊이 우선 탐색) 사용
  • DFS 함수에서 상하좌우로 이동하면서 주변에 있는 친구(P)를 찾는다.
  • DFS 함수는 재귀적으로 호출
  • 방문하지 않은 위치에 대해서만 이동(방문처리 필요)하고 친구를 찾으면 result++

3. 풀이

3.1. 변수 선언 및 초기화

• N: 캠퍼스의 가로 크기
• M: 캠퍼스의 세로 크기
• campus: 캠퍼스의 상태를 저장하는 이차원 배열
• visit: 각 위치의 방문 여부를 저장하는 이차원 배열

N = sc.nextInt(); 
M = sc.nextInt(); 

campus = new char[N][M]; // 캠퍼스 
visit = new boolean[N][M]; // 방문처리

3.2. 캠퍼스 배열 입력 및 도연이의 위치 좌표 저장

• 캠퍼스의 상태를 입력받아 campus 배열에 저장
• 도연이의 위치를 찾아 r과 c 변수에 저장

//도연이 위치에 대한 변수
int r = 0;
int c = 0;

//입력 처리
for(int i=0;i<N;i++) {
	String s = sc.next();
	for(int j=0;j<M;j++) {
		campus[i][j] = s.charAt(j);
		//도연이 위치를 저장
		if(campus[i][j]=='I') {
		r = i;
		c = j;
		}
	}
}

3.3. DFS 수행

• 도연이의 위치에서 시작하여 상하좌우로 이동하면서 주변에 있는 친구들을 찾는다.
• visit 배열을 사용하여 이미 방문한 위치를 체크하며 방문처리를 함께 진행한다.
• 만나는 사람(P)을 찾을 때마다 result++

//DFS 수행
DFS(r,c);
...
	public static void DFS(int x, int y) {
		visit[x][y] = true;

		if(campus[x][y]=='P') result++;

			for(int i=0;i<4;i++) {
				int nx = x + dx[i];
            	int ny = y + dy[i];

            	if(nx>=0 && ny >=0 && nx<N && ny<M && !visit[nx][ny]) {
                	if(campus[nx][ny]!='X') {
                    	DFS(nx,ny);
                	}
            	}
        	}
    	}
	}

3.4. 결과 출력

• 만난 사람이 없는 경우 "TT"를 출력
• 그렇지 않은 경우에는 만난 사람의 수 출력

if(result==0) {System.out.println("TT");} //만난 사람이 없는경우 TT 출력
else {System.out.println(result);} // 만난 사람이 있으면 result 출력

4. 전체코드

import java.util.*;

public class Main {
    static int N; // 캠퍼스 가로
    static int M; // 캠퍼스 세로

    static char[][] campus; // 캠퍼스
    static boolean[][] visit; // 방문처리

    static int[] dx = {-1, 1, 0, 0}; // 상하좌우
    static int[] dy = {0, 0, -1, 1}; // 상하좌우

    static int result = 0; // 만나는 사람 수

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        N = sc.nextInt(); 
        M = sc.nextInt(); 

        campus = new char[N][M]; // 캠퍼스 
        visit = new boolean[N][M]; // 방문처리

        //도연이 위치에 대한 변수
        int r = 0;
        int c = 0;

        //입력 처리
        for(int i=0;i<N;i++) {
            String s = sc.next();
            for(int j=0;j<M;j++) {
                campus[i][j] = s.charAt(j);
                //도연이 위치를 저장
                if(campus[i][j]=='I') {
                    r = i;
                    c = j;
                }
            }
        }

        //DFS 수행
        DFS(r,c);
        
        if(result==0) {System.out.println("TT");} //만난 사람이 없는경우 TT 출력
        else {System.out.println(result);} // 만난 사람이 있으면 result 출력

    }

    public static void DFS(int x, int y) {
        visit[x][y] = true;

        if(campus[x][y]=='P') result++;

        for(int i=0;i<4;i++) {
            int nx = x + dx[i];
            int ny = y + dy[i];

            if(nx>=0 && ny >=0 && nx<N && ny<M && !visit[nx][ny]) {
                if(campus[nx][ny]!='X') {
                    DFS(nx,ny);
                }
            }
        }
    }
}

DFS(깊이 우선 탐색) Review

• 그래프나 트리와 같은 자료 구조에서 한 정점으로부터 시작하여 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 알고리즘
• 주로 그래프 탐색, 연결 요소 찾기, 위상 정렬, 미로 찾기 등에 사용

DFS의 주요 특징과 과정

• 재귀나 스택을 활용한 구현
  • 재귀를 사용하면 코드가 간결해지지만, 스택을 명시적으로 사용할 수도 있습니다.
• 한 정점에서 최대한 깊게 탐색
  • 시작 정점에서 한 분기를 끝까지 탐색하고, 그 다음 분기로 넘어가기 전에 해당 분기의 모든 정점을 방문
• 스택을 이용한 후입 선출 방법
  • 스택을 사용할 경우, 가장 나중에 방문한 정점을 가장 먼저 처리하는 후입 선출(Last In First Out) 방식을 따른다.
• 방문한 정점을 표시
  • 각 정점을 방문할 때마다 방문한 것으로 표시하여 무한 루프를 방지
• 재귀 호출을 통한 자연스러운 구현
  • 재귀를 사용하면 현재 정점에서 다음 정점으로 이동하는 부분을 함수 호출로 자연스럽게 표현할 수 있습니다.