[BOJ] 1149 - RGB거리 (Java)

알고리즘 분류

• 다이나믹 프로그래밍

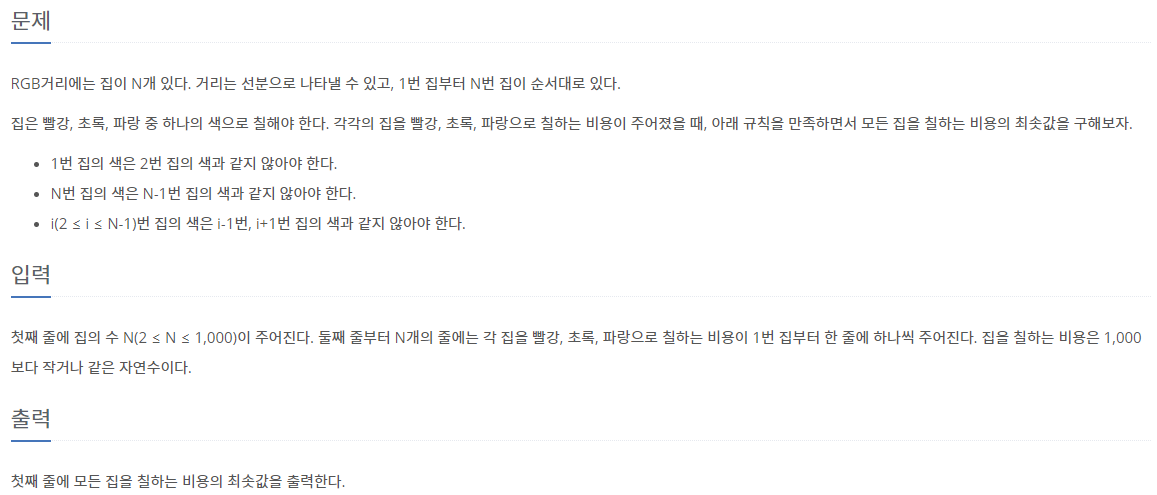
1. 문제

각 집을 빨강, 초록, 파랑 중 하나로 칠하는 비용이 주어지고, 인접한 집은 같은 색으로 칠할 수 없을 때, 모든 집을 칠하는데 드는 최소 비용을 찾는 문제

2. Idea

• 각 집마다 이전 집까지의 최소 비용을 구하면서 현재 집을 칠하는데 드는 최소 비용을 계산 (다이나믹 프로그래밍)

• 마지막 집에서는 빨강, 초록, 파랑 중에서 가장 적은 비용을 선택하여 모든 집을 칠하는데 드는 최소 비용 도출

3. 풀이

3.1. Scanner 입력 및 변수 선언

• n = 집의 수

Scanner sc= new Scanner(System.in);
int n = Integer.parseInt(sc.nextLine());

3.2. dp 배열 생성

• dp : 은 각 집을 빨강, 초록, 파랑으로 칠하는 비용의 최소값을 저장한 2차원 배열.

• dp[i][j]: i번째 집을 j색으로 칠하는데 드는 최소 비용

int[][] dp = new int[n+1][3];

3.3. 최소 비용 계산

• for문을 통해 각 집에 대한 비용을 입력받고, dp 배열 계산

• 각 집을 빨강, 초록, 파랑으로 칠하는데 드는 비용= 이전 집의 다른 두 색 중에서 최소 비용을 + 현재 집의 비용

for (int i = 1; i <= n; i++) {
	StringTokenizer st = new StringTokenizer(sc.nextLine());
    int r = Integer.parseInt(st.nextToken());
    int g = Integer.parseInt(st.nextToken());
    int b = Integer.parseInt(st.nextToken());

    dp[i][0] = Math.min(dp[i - 1][1], dp[i - 1][2]) + r;
    dp[i][1] = Math.min(dp[i - 1][0], dp[i - 1][2]) + g;
    dp[i][2] = Math.min(dp[i - 1][0], dp[i - 1][1]) + b;
}

3.4. 가장 적은 비용 출력

System.out.println(Math.min(dp[n][0], Math.min(dp[n][1], dp[n][2])));

4. 전체코드

import java.util.*;
public class BOJ_1149 {
    public static void main(String[] args) {
        Scanner sc= new Scanner(System.in);
        int n = Integer.parseInt(sc.nextLine());

        int[][] dp = new int[n+1][3];

        for (int i = 1; i <= n; i++) {
            StringTokenizer st = new StringTokenizer(sc.nextLine());
            int r = Integer.parseInt(st.nextToken());
            int g = Integer.parseInt(st.nextToken());
            int b = Integer.parseInt(st.nextToken());

            dp[i][0] = Math.min(dp[i - 1][1], dp[i - 1][2]) + r;
            dp[i][1] = Math.min(dp[i - 1][0], dp[i - 1][2]) + g;
            dp[i][2] = Math.min(dp[i - 1][0], dp[i - 1][1]) + b;
        }
        System.out.println(Math.min(dp[n][0], Math.min(dp[n][1], dp[n][2])));
    }
}