[BOJ] 1929 - 소수 구하기 (Java)

알고리즘

• 수학

• 정수론

• 소수 판정

• 에라토스테네스의 체

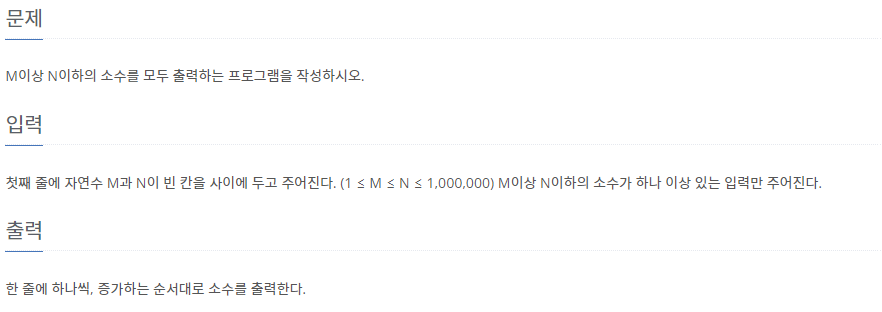
1. 문제

2. Idea

2.1. 시간초과 이슈 발생

import java.util.*;
public class BOJ_1929 {
    public static void main(String[] args) {
        Scanner sc=new Scanner(System.in);
        int n1=sc.nextInt();
        int n2=sc.nextInt();
        while(n1<=n2){
            boolean tf=false;
            for(int i=2; i<n1; i++){
                if(n1%i==0){tf=true; break;}
            }
            if(tf==false){System.out.println(n1);}
            n1++;
        }

    }
}

2.2. 시간초과 이유

• 소수를 판별할 때 모든 수에 대해 2부터 n1-1까지 나눠보는 브루트 포스 방식을 사용
  • 이 방식은 n1과 n2 사이의 모든 수에 대해 소수 판별을 수행하므로, 시간 복잡도가 매우 높아짐.

2.3. 문제 해결

• 에라토스테네스의 체

에라토스테네스의 체: 소수를 판별하는 알고리즘으로, 소수를 대량으로 빠르고 정확하게 구할 수 있다.

가장 먼저 소수를 판별할 범위만큼 배열을 할당하여, 해당하는 값을 넣어주고, 이후에 하나씩 지워나가는 방법을 이용

1. 배열을 생성하여 초기화한다.

2. 2부터 시작해서 특정 수의 배수에 해당하는 수를 모두 지운다.(지울 때 자기자신은 지우지 않고, 이미 지워진 수는 건너뛴다.)

3. 2부터 시작하여 남아있는 수를 모두 출력한다.

https://blog.naver.com/ndb796/221233595886

3. 풀이

3.1. eratos() 메서드 구현

• eratos 메서드 = 에라토스테네스의 체 알고리즘

• primes[0]과 primes[1]을 true로 설정하여 0과 1을 소수가 아님을 표시

• for 반복문을 사용하여 2부터 Math.sqrt(primes.length)까지 모든 수에 대해

  • primes[i]==true -> 소수가 아님으로 처리

  • 그렇지 않으면, i의 제곱부터 시작하여 i의 배수들을 모두 소수가 아님으로 표시

 public static void eratos(){
	primes[0]=primes[1]=true; //0,1은 소수가 아님.

	for(int i=2; i<=Math.sqrt(primes.length);i++){
		if(primes[i]){continue;}
		for(int j=i*i;j< primes.length;j+=i){primes[j]=true;}
    }
}

3.2. 변수 선언 및 배열 초기화

• primes=인덱스에 대응하는 숫자가 소수인지 아닌지에 대한 여부

• m, n=찾고자 하는 소수의 범위

• primes 배열 n까지의 크기로 초기화

int m=sc.nextInt();
int n=sc.nextInt();
primes=new boolean[n+1];

3.3. eratos() 실행

• 에라토스테네스의 체 알고리즘을 실행하여 primes 배열을 업데이트

eratos();

3.4. 소수 판별 및 결과 출력

• for 반복문을 사용하여 m부터 n까지의 모든 숫자에 대해

  • primes[i]==false (i가 소수인 경우) -> print

for(int i=m; i<=n; i++){
	//false->소수
	if(!primes[i]){System.out.println(i);}
}

• 에라토스테네스의 체 알고리즘으로 모든 소수를 찾아내었으므로, 범위 내의 모든 소수가 출력됨

4. 전체코드

public class BOJ_1929 {
    public static boolean[] primes;
    public static void main(String[] args) {

        Scanner sc=new Scanner(System.in);
        int m=sc.nextInt();
        int n=sc.nextInt();
        primes=new boolean[n+1];
        eratos();

        for(int i=m; i<=n; i++){
            //false->소수
            if(!primes[i]){System.out.println(i);}
        }
    }

    public static void eratos(){
        primes[0]=primes[1]=true; //0,1은 소수가 아님.

        for(int i=2; i<=Math.sqrt(primes.length);i++){
            if(primes[i]){continue;}
            for(int j=i*i;j< primes.length;j+=i){primes[j]=true;}
        }
    }
}