[BOJ] 2240 - 자두나무 (Java)

알고리즘

• 다이나믹 프로그래밍

1. 문제

//예제 입력
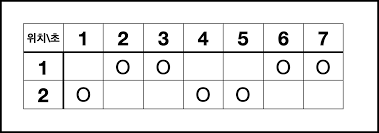
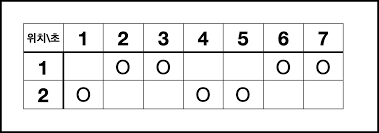
7 2
2
1
1
2
2
1
1

//예제 출력
6

2. Idea

• dp[자두(사람) 위치][시간][이동 횟수]

• 점화식

//T초 시점에서 자두가 1번 나무 밑으로 떨어지는 경우
dp[1][i][j]=Math.max(dp[1][i-1][j],dp[2][i-1][j-1])+1; //현재 위치==1(자두를 받음)
dp[2][i][j]=Math.max(dp[2][i-1][j],dp[1][i-1][j-1]); //현재 위치==2(자두를 받지 못함)

//T초 시점에서 자두가 2번 나무 밑으로 떨어지는 경우
dp[1][i][j]=Math.max(dp[1][i-1][j],dp[2][i-1][j-1]); //현재 위치==1(자두를 받지 못함)
dp[2][i][j]=Math.max(dp[2][i-1][j],dp[1][i-1][j-1])+1; //현재 위치==2(자두를 받음)

3. 풀이

3.1. 변수 선언 및 초기화

• T: 시간, W: 이동 횟수

• arr[ ]: index에 따른 값==T에 따른 자두가 떨어지는 위치

• dp[ ]: [현재 위치][시간][이동 횟수]

private static int T, W;
private static int[] arr;
private static int[][][] dp; //[현재 위치][시간][이동 횟수]

3.2. 입력값 배열에 삽입

arr=new int[T+1]; //T+1-> 반복문에서 모두 입력된 뒤의 크기==총 시간 수 + 나무 위치 수
for(int i=1; i<=T; i++){ //index 0에는 이미 T가 삽입되어 있으므로 i는 1부터 시작
  	arr[i]=Integer.parseInt(sc.nextLine());
    //arr=[T, 1,2,2,1,1,...] index에 따른 값==T에 따른 자두가 떨어지는 위치
}

3.3. dp 배열 선언 및 크기 지정

dp=new int[3][T+1][W+2];

• 위치에 대한 배열 크기가 3인 이유: 0 제외, 1: 1번 나무, 2: 2번 나무에 위치 ->index를 이용하기 위함

• W 크기 == W+2, index 0~W+1인 이유

  • index 1~W==자두(사람)이 이동한 횟수

  • index W+1 반복문에서 index(j=1부터 시작),j-1을 고려(W+1 -1 -> W).

3.4. 점화식에 따라 dp 배열 생성

for(int i=1; i<=T; i++){ //1초부터 T초까지 반복
	for(int j=1; j<=W+1; j++){ //자두가 떨어지는 나무 위치만큼 반복(T초 동안)
		//dp[현재 위치][시간][이동 횟수]
		if(arr[i]==1){ //T초 시점에서 자두가 1번 나무 밑으로 떨어지는 경우
			dp[1][i][j]=Math.max(dp[1][i-1][j],dp[2][i-1][j-1])+1; //현재 위치==1(자두를 받음)
			dp[2][i][j]=Math.max(dp[2][i-1][j],dp[1][i-1][j-1]); //현재 위치==2(자두를 받지 못함)
		}
		else{ //T초 시점에서 자두가 2번 나무 밑으로 떨어지는 경우
			if (i == 1 && j == 1) continue; //[0,2][1][1] 건너뜀. 배열의 초기값은 항상 0이다.
			//1초 시점, 자두(사람)을 이동시키지 못함.-> 현재 위치가 1인 경우 -> dp 초기 단계는 건너 뜀
			dp[1][i][j]=Math.max(dp[1][i-1][j],dp[2][i-1][j-1]); //현재 위치==1(자두를 받지 못함)
			dp[2][i][j]=Math.max(dp[2][i-1][j],dp[1][i-1][j-1])+1; //현재 위치==2(자두를 받음)
		}
	}
}

3.5. 결과 출력

• dp 배열 순회 max값 출력

int result=0;
for(int i=1; i<=W+1; i++){ // dp 전체 순회
	result=Math.max(result, Math.max(dp[1][T][i],dp[2][T][i]));
}
System.out.println(result);

4. 전체코드

//Gold_자두나무
import java.util.*;
public class BOJ_2240 {
	//  T: 시간, W: 이동 횟수
    private static int T, W;
    private static int[] arr;
    private static int[][][] dp; //[현재 위치][시간][이동 횟수]

    public static void main(String[] args) {
        Scanner sc=new Scanner(System.in);
        StringTokenizer st=new StringTokenizer(sc.nextLine());
        T=Integer.parseInt(st.nextToken());
        W=Integer.parseInt(st.nextToken());
        
        arr=new int[T+1]; //T+1-> 반복문에서 모두 입력된 뒤의 크기==총 시간 수 + 나무 위치 수
        for(int i=1; i<=T; i++){ //index 0에는 이미 T가 삽입되어 있으므로 i는 1부터 시작
            arr[i]=Integer.parseInt(sc.nextLine());
            //arr=[T, 1,2,2,1,1,...] index에 따른 값==T에 따른 자두가 떨어지는 위치
        }

        dp=new int[3][T+1][W+2];
        //위치에 대한 배열 크기가 3인 이유: 0 제외, 1: 1번 나무, 2: 2번 나무에 위치 ->index를 이용하기 위함
        //W 크기 == W+2, index 0~W+1인 이유
        //index 1~W==자두(사람)이 이동한 횟수
        //index W+1 반복문에서 index(j=1부터 시작),j-1을 고려(W+1 -1 -> W).

        for(int i=1; i<=T; i++){ //1초부터 T초까지 반복
            for(int j=1; j<=W+1; j++){ //자두가 떨어지는 나무 위치만큼 반복(T초 동안)
                //dp[현재 위치][시간][이동 횟수]
                if(arr[i]==1){ //T초 시점에서 자두가 1번 나무 밑으로 떨어지는 경우
                    dp[1][i][j]=Math.max(dp[1][i-1][j],dp[2][i-1][j-1])+1; //현재 위치==1(자두를 받음)
                    dp[2][i][j]=Math.max(dp[2][i-1][j],dp[1][i-1][j-1]); //현재 위치==2(자두를 받지 못함)
                }
                else{ //T초 시점에서 자두가 2번 나무 밑으로 떨어지는 경우
                    if (i == 1 && j == 1) continue; //[0,2][1][1] 건너뜀. 배열의 초기값은 항상 0이다.
                    //1초 시점, 자두(사람)을 이동시키지 못함.-> 현재 위치가 1인 경우 -> dp 초기 단계는 건너 뜀
                    dp[1][i][j]=Math.max(dp[1][i-1][j],dp[2][i-1][j-1]); //현재 위치==1(자두를 받지 못함)
                    dp[2][i][j]=Math.max(dp[2][i-1][j],dp[1][i-1][j-1])+1; //현재 위치==2(자두를 받음)
                }
            }
        }

        int result=0;
        for(int i=1; i<=W+1; i++){ // dp 전체 순회
            result=Math.max(result, Math.max(dp[1][T][i],dp[2][T][i]));
        }
        System.out.println(result);
    }
}