해당 글은 이득우의 게임 수학을 내 입맛대로 정리한 글이다.

이전에 공부했던 벡터와 스칼라는 벡터 공간 내부에서 덧셈, 곱셈의 연산을 활용해 벡터의 움직임과 힘을 구현해 직선 움직임을 표현했다면, 삼각함수는 원을 기반으로 한 회전을 처리할 때 사용하는 연산이라고 할 수 있다.

삼각함수

삼각함수를 잘 표현하는 예시 중 하나는 바로 직각삼각형이다.

직각 삼각형의 구성요소는 각각 빗변(직각의 대변으로 그냥 대각선으로 뻗어있는 변을 얘기함), 밑변, 높이 3가지로 구성이 되어있다.

밑변과 높이 사이의 각이 직각이기에 나머지 두개의 각도는 90도보다 작은 예각이 되어야한다.

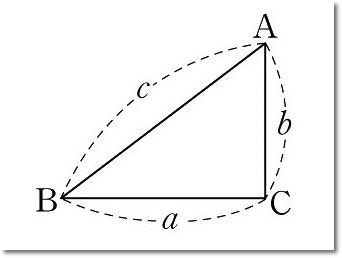
위 그림을 통해 조금 더 구체적으로 설명한다면, a는 밑변, b는 높이, c는 빗변이다. a와 b 사이의 각도는 90도이고 나머지 2개의 각은 90보다 작은 예각을 소유하고 있다.

삼각비

이런 직각삼각형 내에 3변 중 2변을 뽑아서 각각의 비례관계를 나타내는 것을 삼각비(Trigonometric Ratio)라고 부르는데 그 종류는 사인(Sine), 코사인(Cosine), 탄젠트(Tangent) 총 3가지로 이루어져 있다. sine은 높이(b) / 빗변(c), cosine은 밑변(a) / 빗변(c), tangent는 높이(b) / 밑변(a) 으로 구성되어있다.

그리고 tangent의 경우는 sine / cosine으로도 표현이 가능하다. 각각 (b / c_, (a / c)이기에 비율상으로는 b / a와 동일하기 때문에 생기는 특징이라고도 할 수 있다.

(ex. 밑변 4, 높이 3, 빗변 5라고 가정했을 때, 3 / 4 = 0.75이고, 3 / 5 = 0.6, 4 / 5 = 0.8 -> 0.6 / 0.8 = 0.75 라는 동일한 결과가 나오게 된다.)

삼각함수 사용

이런 삼각비를 기반으로 직각삼각형을 좌표계에 배치하고 사잇각의 범위를 실수 전체로 확장하는 대응 관계를 삼각 함수라고 정의한다.

말이 실수 전체로 확장하는 대응 관계라고 하지만 그냥 좌표평면계에 배치해서 사용한다고 생각하면 된다. 실수 전체의 확장에 대한 얘기는 좌표계가 실수 자체를 사용하기 때문에 나온 말이라고 할 수 있다.

보통 삼각함수를 사용할 때는 좌표계에 원을 그려서 많이 표현하기도, 사용하기도 한다.

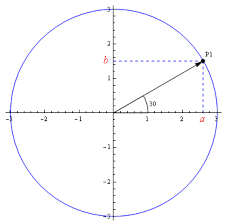
위의 그림 처럼 원을 기반으로 특정 좌표인 P1을 찍었을 때 그것을 쭉 밑으로 내려 a라는 위치에 닿게 되면 높이가 생기고 그 위치가 표현이 된다. 밑변도 동일하게 오른쪽으로 가 b라는 좌표에 닿게 될 때 0부터 a까지의 거리가 나오게 된다.

이런 상황에서 추가로 빗변이 1이라고 가정할 때 높이와 빗변을 바로 구할 수 있는데, 높이를 a, 밑변을 b라고 가정한다면 sin(A) = a / 1 = a; cos(A) = b / 1 = b;가 되기에 높이는 sin(A), 너비는 cos(A)가 될 수 있다는 사실 또한 증명이 된다.

여기서 피타고라스 정리까지 같이 응용해보면 a^2 + b^2 = c^2를 현재 상황에 대입시키게 된다면 sin(A)^2 + cos(A)^2 = 1이라는 결론 또한 나오게 된다.

그럼 이와같은 상황에서 빗변이 1이 아닌 r이라는 실수가 되는 경우는 위의 공식들과 비례해서 같이 증가하기 때문에 r^2 * sin(A)^2 + r^2 * cos(A)^2 = r^2라는 결과도 같이 나오게 된다. 이 공식은 생각보다 많이 사용되기 때문에 외워두는 것이 정말 도움이 될 것으로 보인다.

삼각함수 성질

데카르트 좌표계 즉 좌표평면에서 각도를 표현할 때는 x축의 양수 쪽에서 원의 궤적을 따라 반시계 방향으로 회전한 크기를 의미한다. 조금 더 쉽게 말하면 보통은 원의 중심은 0,0이고 원의 반지름이 r이라고 한다면 r, 0 좌표에서 부터 n도 만큼의 각도를 이동하면서 회전 크기를 표시할 수 있다.

예를 들어 좌표가 (1, 0)이라고 한다면 (cos(0), sin(0))이 된다. cos, sin 순서인 이유는 너비 위치가 x이고 높이 위치가 y이기 때문이다.

cos(0) = 1(밑변) / 1(빗변) = 1, sin(0) = 0(높이) / 1(빗변) = 0으로 계산할 수 있다.

sin 함수는 0에서 90까지 각도가 늘어나면서 높이가 증가하기 때문에 크기가 점점 증가하는 특징을 가지고 있다. 반대로 cos는 대각선이 올라가면 올라갈 수록 빗변의 길이가 같다면 밑변의 길이가 작아지기 때문에 cos의 크기가 0에 더 가까워지는 점점 더 작아진다는 특징을 가지게 된다.

sin의 경우 90도가 넘을 때 270가 될 때 까지 -1에 가까워 진다. 그리고 360, 450도까지 점점 커져 다시 1이 되는 패턴을 반복하고 cos 함수는 sin과 비슷하지만 180도일 때 -1이 되고 360도일 때 1이 되는 특징을 가지고 있다.

자세한 이유는 직접 계산해보면 더 빠르니 아래와 같은 그래프 처럼 동작하는 것을 기억하는 것이 좋다.

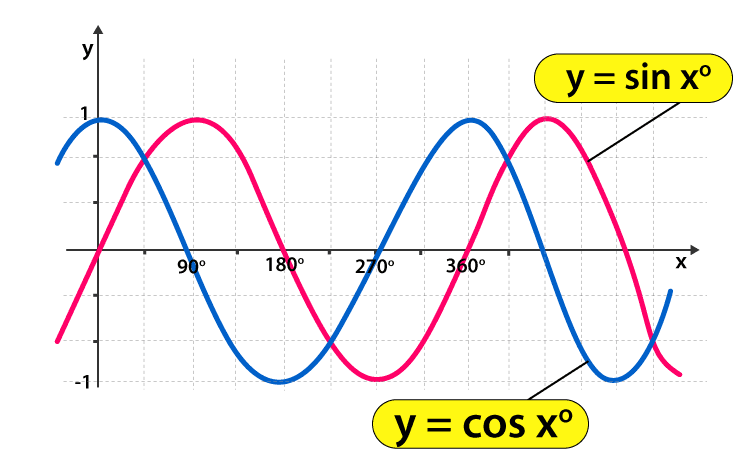
여담으로 1 ~ -1까지의 변화하는 값의 범위를 진폭 반복되는 각도를 주기 라고 부른다.

정리

삼각함수의 성질은 조금 더 간결하게 정리해보자면 다음과 같은 3가지 성질을 가진다고 정의하면 좋다.

1. sin 함수와 cos 함수는 항상 -1에서 1 사이를 일정하게 반복하는 패턴을 의미한다.
2. sin 함수와 cos 함수의 값은 360 주기로 반복된다.
3. y축 기준으로 좌우를 접어 포갠다면 cos 함수 그래프는 데칼코마니 처럼 좌우가 대칭된다면, sin 함수는 상하가 반전된 원점 대칭의 형태를 띈다.
   3-1. cos 함수 처럼 좌우가 대칭인 경우를 짝함수 또는 우함수라고 부르며 sin 함수 처럼 원점 기준으로 대칭의 성질을 가진 것을 홀함수 혹은 기함수라고 부른다.
   3-2. 3-1의 특징에 기반하여 다음과 같은 공식이 성립하게 된다.

   cos(-A) = cos(A) -> cos(90) = 0, cos(-90) = 0 이라는 것을 기억하면 도움이 된다.
   sin(-A) = -sin(A) -> sin(-90) = -1, sin(90) = 1 이라는 것을 기억하면 좋다. sin(90)이 1이기에 -sin(90) = sin(-90)이다.

3-3. 3-2에서 나오는 공식을 조금 더 확장해서 생각해본다면 다음과 같은 공식이 성립하게 된다.

cos(360 - A) = cos(A) -> cos(270) = 0, cos(90) = 0 두개가 같음이 성립된다.

이 cos 공식의 경우는 서로가 바라보는 지를 검사하는 것에도 굉장히 유용하다고 할 수 있다. 서로를 바라본다라는 것은

각각의 각도가 서로 상반됨을 의미하게 된다. (그림이 이상한 것은 이해해달라 직접 그려서 그렇다)

그리고 이것은 빨간색의 cos(330) = 0.8660254038, cos(30) = 0.8660254038로 값이 동일함을 알 수 있다.

3-3-1. 프로그래밍 언어 단위로 출력 시 이상한 값이 나와요.
JS나 C++ 같은 언어들에서 Math 기반의 삼각함수를 호출할 때 입력하는 값은 각도가 아닌 radian 단위의 값을 입력하게 된다.

도와 라디안의 계산 방식은 다음과 같다

1도 = PI(3.1415~~~) / 180 Radian
1라디안 = 180 / PI 도
즉 각도 -> 라디안으로 변경할 것이라면 (도 * PI) / 180으로 계산하면 좋다.

Radian은 1당 57.3도를 가지고 있으며 Math.cos(1) = Math.cos(-1)은 동일한 값을 가지고 있지만 Math.cos(30)은 Math.cos(330)과 동일한 값을 가지고 있지 않음을 참고하면 좋다.

그렇기 때문에 만약 사용할 것이라면 위와 같은 계산을 기반으로 돌아가기 때문에 30도 = 0.5235~ 라디안, 330도 = 5.7595~ 라디안 이라는 것을 인지하고 개발할 때 참고하면 좋다.

tan 함수 특징

tan 함수의 경우는 빗변과 무관하고 단순하기 때문에 따로 제외하게 되었는데 위에서 설명했던 대로 tan(a) = sin(a) / cos(a)라는 것을 알고가면 좋다. 분모는 0이 된다면 값이 무한대가 되기 때문에 cos값이 0이 되는 cos(90), cos(270)의 경우 tan(90), tan(270)은 값이 존재하지 않음을 알면 된다.

각 측정 방법

일상생활에서 각도 측정 시 각도법(degree)로 측정하게 되는데 최고 많은 각도인 360을 표준으로 삼기에는 너무 크다. 그렇기 때문에 벡터도 1크기 단위 지정한 것 처럼 위에서 잠시 설명한 Radian(호도법)을 기준으로 각을 측정한다.

호도값을 계산하는 방법은 말 그래도 호가 기준이 된다.

일반적인 반원의 호 (테두리)를 하나의 직선으로 늘여둬서 그 값을 계산해본다면 PI(3.14...) 즉 원주율 값이 나온다. 원주율이라는 것은 곧 반원의 호 값을 의미하는 것 이 된다.

반대로 호도값 1radian은 부채꼴 모양의 호 (테두리)가 1일 때 부채꼴의 각도를 의미하며 그 각도가 57.2958... 도 정도가 나온다.

상관관계

위에서 이미 호도법과 각도법의 parsing 방법에 대해 얘기했으니 흔히 사용하는 각의 각도와 호도에 관해 정리해보자면

각도법	호도법
30도	PI / 6
45도	PI / 4
60도	PI / 3
90도	PI / 2
180도	PI
360도	PI * 2

정도로 기억해두면 도움이 될 것 같다.