[프로그래머스] 게임 맵 최단거리(Java)

게임 맵 최단거리

해결 방법

저는 BFS와 다익스트라(dijkstra) 2가지 방법을 이용해서 해결했습니다.😁

BFS는 가중치가 동일한 최단경로를 찾을 때 매우 유리한 알고리즘 입니다.

그 이유는 BFS는 모든 경우의 수를 따져가며 탐색을 하기 때문에 도착점 도달하면 바로 탈출이 가능하기 때문입니다.^^
(현재 노드에서 가까운 곳부터 찾기 때문에 경로를 탐색 시 먼저 찾아지는 해답이 곧 최단거리 입니다.)

다익스트라(dijkstra)는 가중치가 양수인 최단경로를 찾을 때 사용할 수 있는 알고리즘 입니다.

이 문제에서는 가중치가 항상 1로 동일하기 때문에 사용할 수 있습니다.^^

🤔 DFS는 사용하면 안되나요?

사용할 수 있습니다!!!!
하지만, DFS로 경로를 검색할 경우 처음으로 발견되는 해답이 최단거리가 아닐 수 있습니다.

DFS는 시작점에서 도착점으로 가는 거의 무한한(♾️) 종류의 길을 모두 탐색해야 합니다.
반면에 BFS는 도착점에 도달한 순간 끝내버리면 되죠.👍

풀이

결과

BFS가 다익스트라(dijkstra)보다 빠른 것을 알 수 있습니다...!!

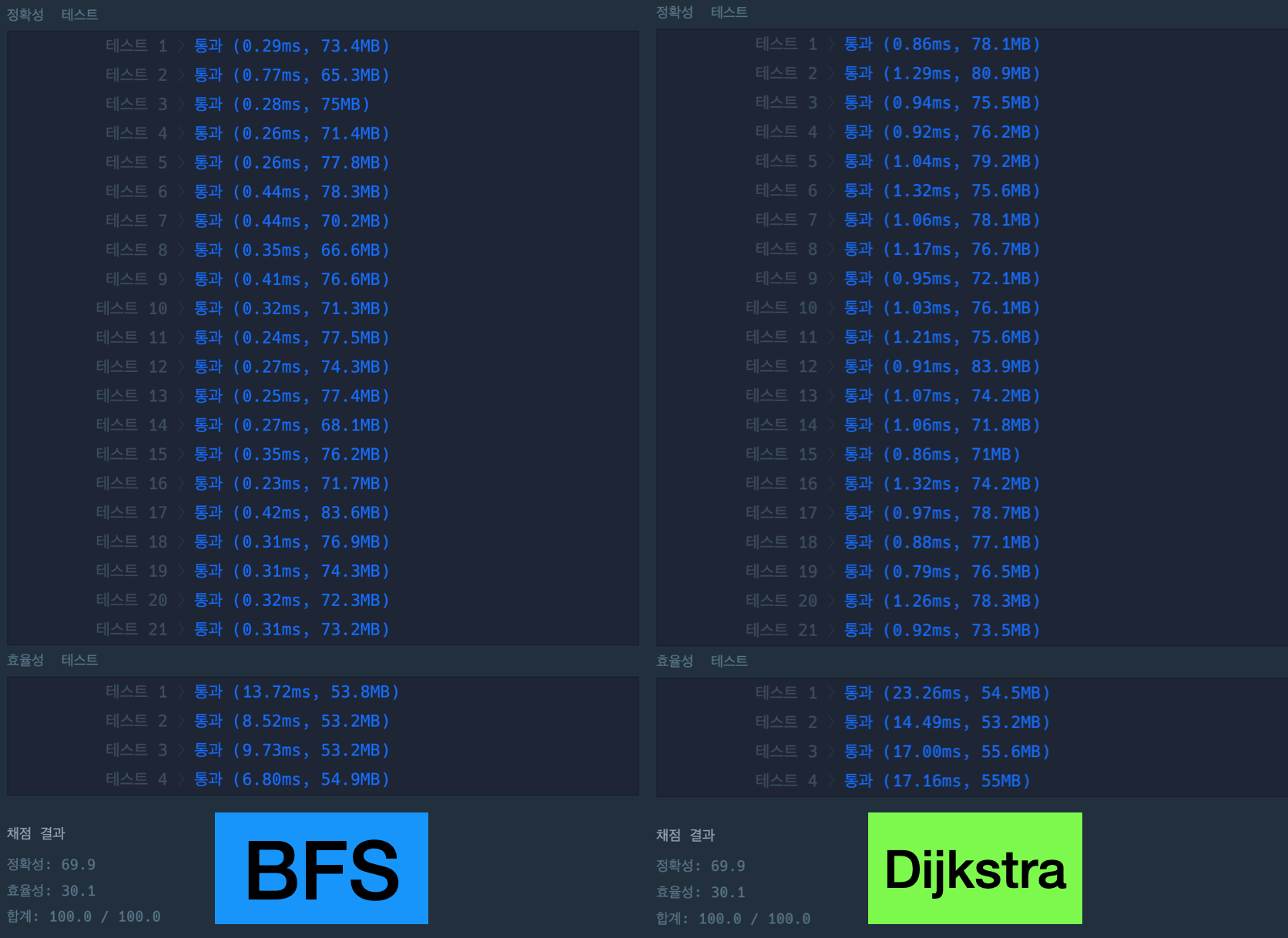
BFS

class Solution {
    public int solution(int[][] maps) {
        int width = maps.length;
        int height = maps[0].length;

        int[][] visited = new int[width][height];


        return bfs(maps, visited, 0, 0, width, height);
    }

    private int bfs(int[][] maps, int[][] visited, int x, int y, int width, int height) {
        Queue<Road> queue = new ArrayDeque<>();
        visited[x][y] = 1;
        queue.offer(new Road(x, y));

        while (!queue.isEmpty()) {
            Road poll = queue.poll();
			  // 상, 하, 좌, 우
            int[] ud = {1, -1, 0, 0};
            int[] lr = {0, 0, 1, -1};

            for (int i = 0; i < 4; i++) {
                int newX = poll.getX() + ud[i];
                int newY = poll.getY() + lr[i];

                // 범위 체크
                if (newX < 0 || newY < 0 || newX >= width || newY >= height) {
                    continue;
                }


                // 방문 이력이 없고, 벽이 아니면
                if(visited[newX][newY] == 0 && maps[newX][newY] == 1) {
                    // 거리 계산
                    visited[newX][newY] = visited[poll.getX()][poll.getY()] + 1;
                    // 목표에 도달하면
                    if(newX == width - 1 && newY == height - 1) {
                        return visited[newX][newY];
                    }

                    queue.offer(new Road(newX, newY));
                }
            }
        }
        return -1;
    }
}
class Road {
    private int x;
    private int y;

    public Road(int x, int y) {
        this.x = x;
        this.y = y;
    }

    public int getX() {
        return x;
    }

    public int getY() {
        return y;
    }

}

다익스트라

static class Solution {
    public int solution(int[][] maps) {
        int width = maps.length;
        int height = maps[0].length;

        // 방문 이력 저장 배열
        boolean[][] visited = new boolean[width][height];

        // 최단 거리 저장 배열 초기화
        int[][] result = new int[width][height];
        for(int i = 0; i < width; i++) {
            for (int j = 0; j < height; j++) {
                result[i][j] = Integer.MAX_VALUE;
            }
        }

        // 인접 리스트 초기화
        List<Road>[][] list = new ArrayList[width][height];
        for(int i = 0; i < width; i++) {
            for(int j = 0; j < height; j++) {
                list[i][j] = new ArrayList<>();
            }
        }

        // 그래프로 변환
        for(int i = 0; i < width; i++) {
            for(int j = 0; j < height; j++) {
                // 벽은 제외
                if(maps[i][j] == 1) {
                    // 가중치가 1
                    list[i][j].add(new Road(i, j, 1));
                }
            }
        }

        int[][] dijkstra = dijkstra(maps, visited, result, list, 0, 0, width, height);

        if(dijkstra[width-1][height-1] == Integer.MAX_VALUE) return -1;

        return dijkstra[width-1][height-1];
    }

    private int[][] dijkstra(int[][] maps, boolean[][] visited, int[][] result, List<Road>[][] list, int startX, int startY, int width, int height) {
        // 가중치를 기준으로 오름차순 정렬
        Queue<Road> pq = new PriorityQueue<>((o1, o2) -> Integer.compare(o1.getWeight(), o2.getWeight()));
        // 초기값 설정
        visited[startX][startY] = true;
        result[startX][startY] = maps[startX][startY];
        pq.offer(new Road(startX, startY, result[startX][startY]));

        while (!pq.isEmpty()) {
            Road poll = pq.poll();
            // 상, 하, 좌, 우
            int[] ud = {1, -1, 0, 0};
            int[] lr = {0, 0, 1, -1};

            for(int i = 0; i < 4; i++) {
                int newX = poll.getX() + ud[i];
                int newY = poll.getY() + lr[i];

                // 범위 체크
                if (newX < 0 || newY < 0 || newX >= width || newY >= height) {
                    continue;
                }

                // 방문 이력이 없으면
                if (!visited[newX][newY]){
                    visited[newX][newY] = true;

                    // road는 newX, newY의 인접 노드
                    for (Road road : list[newX][newY]) {
                        // 최단 거리 계산
                        int min = Math.min(result[poll.getX()][poll.getY()] + road.getWeight(), result[road.getX()][road.getY()]);
                        result[road.getX()][road.getY()] = min;
                        pq.add(new Road(road.getX(), road.getY(), min));
                    }
                }
            }
        }

        return result;
    }
}

static class Road {
    private int x;
    private int y;
    private int weight;

    public Road(int x, int y, int weight) {
        this.x = x;
        this.y = y;
        this.weight = weight;
    }

    public int getX() {
        return x;
    }

    public int getY() {
        return y;
    }

    public int getWeight() {
        return weight;
    }
}