211123, 자료구조 Ch 06-2

오늘은 Ch.6의 복습을 끝내고 진도를 나가보겠다.

그리고 예정상으론 오늘부터는 자료구조와 Cpp를 함께 공부하려고 한다. 힘내보자 나.

Ch. 06-2. 스택의 연결리스트 기반 구현 및 계산기 프로그램 구현

06-3

어제는 배열을 기반으로 Stack을 구현했고, 오늘은 연결 리스트를 기반으로 Stack을 구현하고자 한다.

그냥 뭐 어려울거 없다. 가장 기본적인 연결리스트에 스택이라는 기능적 특수함? 만 가미해주면 된다.

출처

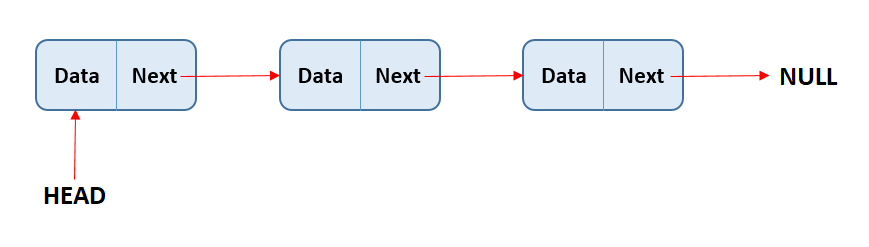
위에 보이는 구조를 써줄거다.

데이터를 넣을때마다 head부분에 새로운 newNode가 삽입되고, 기존에 존재하던 노드들은 하나씩 뒤로 밀려가는 과정으로 데이터를 넣어줄거다.

그러면 나중에 데이터를 빼낼 때에도 (Pop 과정) head부분에 있는 노드가 빠져나오겠지.

그러면, 스택을 위한 헤더파일을 짜보자.

언제나 그랬듯 자세한 설명은 주석으로 달겠다.

/* LBS.h */

#ifndef __L_B_S_H__
#define __L_B_S_H__

#define TRUE	1
#define FALSE	0

typedef int Data;

typedef struct _node {
    Data data;
    struct _node *next;
} Node; // 그냥 노드임

typedef struct _lbs { // 리스트 기반으로한 스택의 struct 정의
    Node *head;
} ListStack;

typedef ListStack Stack;

void StackInit (Stack *pstack);
int SIsEmpty (Stack *pstack);

void SPush (Stack *pstack, Data data);
Data SPop (Stack *pstack);
Data SPeek (Stack *pstack);

#endif

뭐 이정도다. 헤더파일은 공부하다보면 손으로 술술 써진다. 본격적으로 헤더파일에 정의한 ADT들을 직접 구현하는게 문제지.

그러면 하나하나 구현해보겠다.

우선, StackInit과 SIsEmpty. 뭐.. 딱히 말할 것도 없다.

void StackInit (Stack *pstack) {
    pstack->head == NULL;
}

int SIsEmpty (*pstack) {
    if (pstack->head == NULL) {
        return TRUE;
    } else return FALSE;
}

그 다음은, SPush와 SPop이다.

void SPush (Stack *pstack, Data data) {

    Node *newNode = (Node *)malloc(sizeof(Node));
    
    newNode->data = data;
    
    newNode->next = pstack->head; // 새 노드의 next가 기존 노드를 가리킨다.
    pstack->head = newNode; // head 포인터가 새 노드를 가리키도록 바꿔준다.
}

int SPop (Stack *pstack) {
    
    Node *rpos = pstack->head; // Pop 할 데이터의 위치 기억
    Data rdata = rpos->data; // Pop 할 데이터
    
    if (SIsEmpty(pstack)) {
        printf("뽑을 게 없는데요\n");
        exit(-1);
    }
    
    pstack->head = pstack->head->next; // 우선 head를 옮겨주고
    free(rpos); // Pop할 데이터의 위치를 free 함수로 해제해준다.
    return rdata; // 데이터 뽑아냄
}

그 다음, 마지막으로 맨 위에 뭐가있나 슬쩍보는 SPeek이다.

Data SPeek (Stack *pstack) {
    if(SIsEmpty(pstack)) {
        printf("볼 것도 없는데요\n");
        exit(-1);
    }
    
    return pstack->head->data;
}

이렇게 위의 내용들을 합쳐주면, 앞서 정의한 LBS.h의 소스파일인 LBS.c가 완성된다. 이로써, List Base Stack 구현 끗.

06-4

이제 Stack 을 활용하여 계산기 프로그램을 구현해보겠다.

그냥 단순히 3+7-5.. 이런 수식들이 아니라 (65)+(6/4) + 82 - (35) 이런 소괄호를 활용한 꽤 복잡한 수식도 계산할 수 있는 계산기를 만들거다.

여기서 핵심 Key Point는

1. 소괄호 파악
2. 연산자 우선순위 파악

이 두개다.

자 드가자!

..라고 하기 전에, 이 교재에서 계산기를 구현하기 위해 필요한 사전정보가 하나 있다. 수식의 표기법 이다.

1. 중위 표기법 (Infix) : 그냥 우리가 아는 거 그대로다. ex) 5+2/7
2. 전위 표기법 (prefix) : ex ) +5/27
3. 후위 표기법 (postfix) : ex ) 527/+

여기서 계산기 프로그램을 만들 때 우리는 후위 표기법을 써줄 것이다.

그래서 우리가 알고 있는 중위 표기법에서 후위 표기법으로 변환하는 과정이 필요한데, 이 과정은 필자가 마스터했다고 당당하게 말할 수 있기 때문에 생략하겠다.

근데 이걸 내가 손으로 끄적여서 변환할수 있으면 뭐하냐. 지금 우리가 배우고 있는 것은 코딩이다. 중위 표기법에서 후위 표기법으로 변환하는 과정을 담은 "코드"를 짤 수 있어야지.

이걸 알아보도록 하자.

void InToPost(char susik[]);

우리가 중위에서 후기로 바꾸는 함수는 위와 같다고 치겠다.

일단은, 위에서 말한 Key Point 두개중, "2. 연산자 우선순위 파악"을 구현해보겠다.

int GetOpPrec (char op) {
    switch(op) {
    case '*' :
    case '/' :
        return 5;
    case '+' :
    case '-' :
        return 4;
    case '(' :
        return 1;
    }
    
    return -1; // 위에 적혀있는 연산자들이 아니면 우선순위 따지기 실패
}

여기서 아마 의문이 들거다.

엥? '(' 를 왜 연산자로 치죠? 쟤가 연산자면 ')'는 왜 없죠?

방금 내가 중위 -> 후위 과정을 생략해서 그렇지, ( 도 연산자로 친다. (가 나오면 그때부터 연산자 stack에 쌓아두고, 소괄호의 끝을 의미하는 ) 를 만나게 되면 소괄호를 제외한 연산자들은 후위표기법으로 바뀐 수식에 들어가게 되고, 소괄호 기호 (와 )는 공중분해된다. 그냥 소괄호는 어떻게 보면 "얘네가 우선순위 우선빠따다"라는 메세지를 취하고 홀연히 사라지는 것이다.

궁금증이 해결됐다면, 이젠 연산자의 우선순위 반환한 값을 비교하여, 진짜 우선순위가 어떻게 서열정리되는지를 알려줄 함수를 짜보자.

int WhoPrecOp(char op1, char op2) {
    
    int op1prec = GetOpPrec(op1);
    int op2prec = GetOpPrec(op2);
    
    if (op1prec > op2prec) return 1; // op1이 op2보다 우선순위가 높다면
    else if (op1prec < op2prec) return -1; // op2가 op1보다 우선순위가 높다면
    else return 0; // 두 개의 우선순위가 같다면
}

자. 그러면 얘들을 통틀어서 InToPost를 구현해 보겠다. 되게 복잡하고 어렵게 생겼지만, 차근차근 주석을 보며 이해해나가자.

/* InToPost.c */

void InToPost(char susik[]) {

  Stack stack; // 이 스택은, 연산자를 쌓아두는 스택이다.
  int susikLen = strlen(susik); // 수식의 길이 값 저장
  char *convExp = (char*)malloc(susikLen+1);
  // 변환된 수식을 담은 공간을 동적할당.

  int i, idx = 0;
  char top, pop0p;
  
  memset(convExp, 0, sizeof(char)*(susikLen+1));
  // 할당 된 배열을 0으로 초기화. 헤더파일 ctype.h에 저장되어 있다.
  StackInit(&stack); //스택 초기화
  
  for (i=0 ; i<susikLen ; i++) {
      tok = susik[i];
      
      if (isdigit(tok)) {
          convExp[i] = tok;
      } else {
          switch(tok) {
              case '(' :
                  SPush(&stack, tok); // tok이 '(' 일때, stack에 넣어준다
                  break;
                  
              case ')' :
                  while(1) { 
                      pop0p = SPop(&stack); //stack에서 연산자를 꺼내서
                      if(pop0p == '(') break;
                      // '(' 를 꺼내기 전까지
                      convExp[idx++] = pop0p;
                      // 후위 연산자로 변환된 수식에 연산자들을 차례대로 집어넣는다.
                  }
                  break;
                  
              case '+' : case '-' :
              case '*' : case '/' :
                  while(!SIsEmpty(&stack) && WhoPrecOp(SPeek(&stack), tok) >= 0)                
                      convExp[idx++] = SPop(&stack);
                  // 만약 stack이 비어있지 않고, stack의 맨 위의 연산자가
                  // tok보다 우선순위가 높거나 같다면, stack의 맨 위의 연산자를
                  // 후위로 변환된 수식에 집어넣는다.
                  
                  SPush(&stack, tok);
                  break;
          }
      }
  }
  while (!SIsEmpty(&stack)) // 스택에 남은 모든 연산자를
      convExp[idx++] = SPop(&stack); // convExp로 이동
  
  strcpy(susik, convExp); // 후위표기로 바뀐 수식을 susik으로 이동
  free(convExp);

}

그러면 이렇게, 중위표기법으로 표기된 수식을 후위표기법으로 바꾸는 함수를 구현했다.

근데 이게 또 후위 표기법으로 바꾼다고 끝이 아니다.

계산기 프로그램이니깐, 계산 해야지.

만약 후위표기법으로 표기된 수식인 " 324*+ "가 있다고 가정하자.

우선, 숫자 세개를 쌓아 올리면 바닥부터 순서대로 3, 2, 4가 될거다. 즉, 4가 가장 위에 (topIndex)에 있단 얘기다.

그러면, 가장 첫 연산은 *. 피 연산자는 위에서부터 두개인 2와 4가 될 것이다.

근데 여기서 알아둬야할 중요한건, 2, *, 4는 " 4 x 2 "가 아니고, " 2 x 4 "다. 즉, 먼저 "A1 x A2"라고 가정했을 때, A2가 먼저 꺼낸 숫자가 되고, A1이 나중에 꺼낸 숫자가 되는 것이다.

이게 *라서 별 상관 없어보이는데, 만약 나누기나 빼기라면 수식의 결과가 아예 달라질 것이다. 그러면 2x4 = 8. 이젠 3, 8과 +만 남게 된다. 그러면 "3 + 8" = 11. 이렇게 계산이 진행되는 것이다.

그러면 이걸 함수로 만들어보자.

int calculate (char susik[]) {
    Stack stack; // 피연산자인 숫자를 저장할 스택이다.
    int susikLen = strlen(susik);
    int i;
    char tok, op1, op2;
    
    StackInit(&stack);
    
    for (i=0 ; i<susikLen ; i++) {
        tok = susik[i]; // 한 문자씩 tok에 저장.
        
        if (isdigit(susik)) { // 뺄게 숫자라면
            SPush(&stack, tok - '0'); // 아스키코드니까 " -'0' " 후에 저장
        } else { // 연산자면
            op2 = SPop(&stack); // 먼저꺼낸게 op2
            op1 = SPop(&stack); // 이후에꺼낸게 op1
            
            switch(tok) {
            
            case '+' :
                SPush(&stack, op1 + op2);
                break;
            
            case '-' :
            	SPush(&stack, op1 - op2);
                break;
                
            case '*' :
                SPush(&stack, op1 * op2);
                break;
                
            case '/' :
                SPush(&stack, op1 / op2);
                break;
            
            }
        }
    }

    return SPop(&stack);
}

-- 21/11/23 일단 여기까지. 나머지 부분은 오늘 (11/23) 학습하고 내일 11/24에 나머지 내용 복습본을 올리도록 하겠다.

-- 21/11/24 --

위에서

1. 중위표기법을 후위표기법으로 바꾸는 함수
2. 후위표기법으로 바뀐 식을 계산하는 함수

이 두개를 구현했고, 이제는 위의 함수들을 계산기로써 모든 기능을 수행해주는 함수로 합칠 차례다.

/* RealCalculate.h */

#ifndef __REAL_CALCULATE_H__
#define __REAL_CALCULATE_H__

int RealCalculate(char susik[]);

#endif

/* RealCalculate.c */

#include <string.h>
#include <stdlib.h>
#include "InToPost.h" // 중위 -> 후위
#include "Calculate.h"

int RealCalculate(char susik[]) {

    int len = strlen(susik);
    int ret; // 계산 결과를 저장할 변수
    char *expcpy = (char *)malloc(sizeof(len+1));
    // 수식을 expcpy에 옮겨 담을거임
    strcpy(expcpy,susik); // 요렇게
    
    InToPost(expcpy); // 중위 -> 후기 바꿔주고
    ret = Calculate(expcpy); // 수식 계산값 ret에 저장
     
    free(expcpy); // expcpy 해제해주고
    return ret; // 결과 리턴

}

여기까지.