타입스크립트 타입 레벨 프로그래밍

왜?

잠시 당신이 나무꾼이라고 가정해 보자
당신은 숲에서 가장 좋은 도끼를 가지고 있고 가장 일 잘하는 나무꾼이다
그런데 어느 날 산신령이 나타나서 나무를 자르는 새로운 언어인 전기톱을 설명서와 함께 주고 떠난다
당신은 사용하는 방법도 모르면서 설명서는 읽지 않고 늘 해온 방식대로 전기톱으로 나무를 두들겨댄다
당신은 새 언어를 이상하게 쓰면서 그것에 익숙해진다
그때, 누군가 나타나서 전기톱의 시동 거는 법을 알려준다

나는 당신 얘기를 하고 있다
당신은 설명서를 읽지 않은 나무꾼이고, 전기톱은 타입스크립트이다
당신은 타입스크립트를 잘 안다고 착각하고 있다
잘 안다고 생각한다면 혹시 이런 경험이 없는지 다시 생각해보길 바란다

• 타입을 작성하지 못해서 any 타입을 쓴다
  • pipe(), curry() 함수를 타입할 수 있는가?
• IDE에서 함수 정의를 따라가다 라이브러리코드의 d.ts를 보고 도망친다
  • 제네릭으로 가득한 라이브러리 타입을 읽을 수 있는가?
  • T extends infer R ? [R] : never 의 의미를 아는가?

이 글은 타입스크립트라는 전기톱의 시동을 거는 법을 알려주는 짧은 설명서이다
타입을 더 깊게 이해하고 쓰고, 읽을 수 있기를 바라는 마음에서 글을 쓴다

⚙️ 타입은 튜링 완전하다

타입스크립트의 타입 시스템은 튜링 완전함이 증명되었다

👨🏻‍🏫 튜링완전성(turing completeness)
어떤 프로그래밍 언어나 추상 기계가 튜링 기계와 동일한 계산 능력을 가진다는 의미이다. 이것은 튜링 기계로 풀 수 있는 문제, 즉 계산적인 문제를 그 프로그래밍 언어나 추상 기계로 풀 수 있다는 의미이다

제한 없는 크기의 기억 장치를 갖는 기계를 만드는 것이 불가능하므로, 진정한 의미의 튜링 완전 기계는 아마도 물리적으로 불가능할 것이다. 그러나, 제한 없이 기억 장치의 크기를 늘려갈 수 있다고 가정할 수 있는 물리적인 기계 혹은 프로그래밍 언어에 대해서는, 느슨하게 튜링 완전하다고 간주한다. 이런 맥락에서, 요즘 나온 컴퓨터들은 튜링 완전하다고 여겨지고 있다.

타입시스템의 튜링완전성 증명 👈 링크

타입 시스템이 튜링 완전하다는것은 우리가 타입레벨에서 프로그래밍을 하고, 문제를 해결할 수 있다는것을 의미한다

예를 들면 타입시스템으로 소코반 게임을 만들 수도 있다!

런타임에 실행되는 코드가 아닌, 타입 시간에 평가(evaluate)되는 코드이다

👨🏻‍🏫 타입 시간
IDE에서 타이핑하는 시간을 의미한다, IDE를 통해서 일종의 REPL을 수행한다
P는 IDE의 커서위에 나타나는 콤보박스이다

이제 타입 시스템에 대해서 깊게 알아보며 어떻게 이것이 가능한지 살펴볼 것이다

📖 타입 시스템

타입 스크립트의 타입 시스템은 작은 순수 함수형 언어다

타입 시스템이 할 수 있는것들

• 함수 ✅
• 분기 - Conditional Branching ✅
• 변수 대입 ✅
• 루프 - Loops ✅
• 동일성 체크 ✅

타입 시스템이 할 수 없는것들

• 변경 가능한 상태 - Mutable state ❌
• 파일 입출력 - I/O ❌
• 고계도 함수 - HOC ❌
  • 트릭을 쓰면 가능하다

이에 대해서 알아보기 이전에 몇가지 짚고 넘어가려한다

공리계

👨🏻‍🏫 공리(axiom)
어떤 한 형식체계에 관한 논의를 위한 전제로 주어진 공리들의 집합을 공리계(公理系)라고 부른다.

공리와 정리가 섞여있긴 하지만 이 챕터의 내용은 따지지 말고 당연한것으로 받아들이자는 의미에서 공리계라고 이름했다

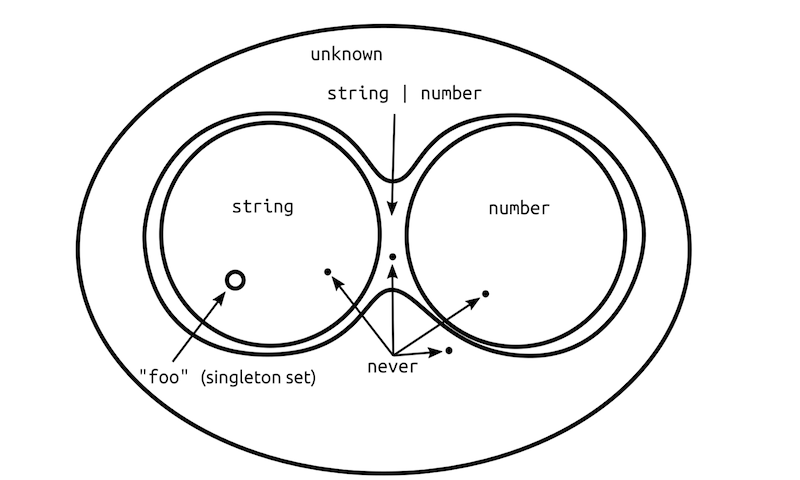
1. 타입은 집합이다

• 타입레벨에서 우리가 항상 다루는것은 집합이다
• number, string 같은 무한 집합이 있다
• A | B은 A와 B의 합집합
• A & B은 A와 B의 교집합
• unknown은 모든집합의 상위집합(superset)이다, 전체집합
• never은 모든집합의 부분집합(subset)이다, 공집합
  • never가 공집합이라는 특성에 의해서 A | never는 A
  • never가 공집합이라는 특성에 의해서 A & never는 never
• any는 모든 타입의 부분집합이자 상위집합이다 🤷
  • A | any는 any
  • A & any는 any

2. 타입으로 데이터를 표현한다

• 다른 언어처럼 데이터를 옮기는것이 가능하다
  • 하지만 이는 타입으로 표현된다
  • 우리가 다룰 데이터는 전부 타입이다!
• 원시자료형
  • boolean
  • number, bigint
  • string, symbol
  • undefined, null
• 리터럴
  • number - ex) 20, 15, 30, ...
  • boolean - ex) true, false
  • string - ex) "hello", "world", ...
  • bigint - ex) 10000n, ...
• 자료구조
  • 오브젝트 - ex) { key: "value" }
  • 튜플 - ex) [1, 2, 3]
  • 리스트 - ex) number[]

함수

타입시스템의 함수는 제네릭이다

/** 런타임에서 실행되는 아래 함수의 타입레벨 프로그래밍 버전
 * const f = (a: A, b: B): A | B => a | b
 */
type F<A, B> = A | B

• 함수명 F1
• 인자 A, B
• 리턴 값 A | B

푸쉬 함수

type Push<X, XS extends X[]> = [...XS, X]

• constraints X[]
  • XS는 X[]의 부분집합으로 제한된다
  • XS가 X[]의 부분집합이다 = XS가 X[]에 대입 가능하다
    • 리스코프 치환원칙
  • XS에 리스트가 아닌 타입이 온다면 IDE는 빨간줄을 표시한다
• spread operator ...XS
  • XS의 원소들을 풀어준다

👨🏻‍🏫 리스코프 치환원칙
자료형의 의미론적 처리를 보장하기 위한 법칙이다
A extends B일 때, B를 A로 대체해도 동작에 문제가 없어야 한다

분기 - Conditional Branching

타입 시스템에서 분기는 conditional types에 의해 구현된다

type IF<A extends boolean, B, C> = 
  A extends true ? B : C

type val1 = IF<true, number, boolean> 👈 number
type val2 = IF<false, number, boolean> 👈 boolean

• 삼항연산자 형식으로 분기를 처리할 수 있다
• 안타깝게도, if-else 를 사용할 수 없다
  • typetype을 이용하면 if-else를 쓰고 ts 코드로 트랜스파일 할 수 있다
• extends가 두번 쓰였는데 두개가 약간 다르다
  1. A extends boolean
  • 앞서 설명한 constraint - A는 boolean의 부분집합
  2. A extends true ? B : C
  • A 가 true의 부분집합인지 테스트한다
    • A가 true에 대입가능한지 테스트하는것과 같다 (리스코프 치환원칙)
  • 테스트결과가 참이라면 B로 분기
  • 테스트결과가 거짓이라면 C로 분기

논리회로

디지털회로, 컴퓨터 구조 등의 과목에서 배운 논리 회로를 전부 구현할 수 있다

👨🏻‍🏫 논리회로(logic circuit)
불 대수(Boolean algebra)를 이용하여 1개 이상의 논리 입력을 일정한 논리 연산에 의해 1개의 논리 출력을 얻는 회로이다
전자 회로(electronic circuit)의 구성 요소들을 이용하여 만든 논리 게이트(NAND, NOR, NOT 등)를 이용해 원하는 동작을 구현하는, 현대의 디지털 시대를 이끈 장본인 격의 학문이다

가독성을 위해 카르노맵을 사용합니다

AND Gate

AND	0	1
0	0	0
1	0	1

type AND<A extends boolean, B extends boolean> = 
  [A, B] extends [true, true] ? true : false

NOT Gate

Not	0	1
always	1	0

type NOT<A extends boolean> =
  A extends true ? false : true

NAND Gate

NAND	0	1
0	1	1
1	1	0

type NAND<A extends boolean, B extends boolean> = 
  NOT<
    AND<A, B>
  >

• NAND 함수(generic type)는 이전에 만든 NOT, AND 함수를 재사용한다
  • 함수는 재사용 가능하다
  • 전자공학에서 모든 논리 게이트는 NAND 만으로 구성 가능하다
  • 즉, 이제 우리는 모든 논리 게이트를 NAND를 재사용해서 구현 가능하다

infer

infer 키워드는 Generic을 위한 Generic이다

인자로 리스트를 받아 길이를 반환하는 함수 LengthOf<T>를 어떻게 구현할 지 생각해보자

인덱스로 접근하기

indexed-access-types를 이용해서 T['length']를 접근하면 될 것 같다

type LengthOf<T> = T['length']

• 이는 보기 좋게 실패한다
  • Type length cannot be used to index type T
• length를 인덱스로 쓸 수 있게 만들어야한다
• 해결법
  1. [] constraint를 쓴다
  2. .length constraint를 사용한다

1. 리스트 constraint 활용

type LengthOf<T extends unknown[]> = T['length']

2. length constraint 활용

type LengthOf<T extends { length: r }> = r

처럼 쓸 수 있다면 좋겠지만 아쉽게도 위의 r표현은 불가능하다

대신 타입스크립트는 infer 키워드를 제공해준다

type L1<T extends { length: infer R}> = R ❌

type L2<T extends { length: unknown}> =
  T extends { length: infer R } ? R : never ✅

• 아쉽게도 L1 방식은 불가능하다
• L2처럼 extends 의 분기검사를 할 때만 사용가능
  • extends의 우측에서만 쓰일 수 있다
  • T 가 { length: infer R }의 부분집합이고 R을 추론가능하면 R로 분기
  • 아니라면 never로 분기

대입하기

type F<T> = [ 
  HeavyComputation<T>,
  HeavyComputation<T>,
  HeavyComputation<T>,
]

type F<T> = 
  HeavyComputation<T> extends infer R ? (
    [R, R, R]
  ) : never 👈 절대 분기되지 않는 상황

• 함수 내에서 변수에 R에 대입하기위해서 infer R을 사용
• never는 절대 분기되지 않을 상황이지만 infer 키워드가 분기 검사를 위한 extends의 우측에서만 쓰일 수 있기 때문에 불가피하게 사용

루프

자료 구조에 따라 달라지는 루프 방법

• Object Types - Mapped Types
• Tuples - Recursive conditional Types
• Unions - Distributive Conditional Types

Mapped Types

type L<T extends Record<string, string>> = {
  [k in keyof T]: `love ${T[k]}`
}
type 결과 = L<{ I: 'you'; you: 'me' }>
// 결과 = { I: 'love you', you: 'love me' }

• in 키워드는 Union 타입을 순회한다
  • keyof T는 Union타입

Recursive Conditional Types

type Includes<X, XS> =
  XS extends [infer First, ...infer Rest] ? (
    First extends X ? true : Includes<X, Rest>
  ) : false

type T = Includes<1, [1, 2, 3]> 👈 true
type F = Includes<4, [1, 2, 3]> 👈 false

• 배열 XS를 구조분해할당 하고 있다
  • 맨 앞과 나머지로 나눠서 나머지를 재귀로 돌린다
  • 선형탐색과 같다
• 아래 코드와 같은 알고리즘이다

const includes = (tar: number, arr: number[]): boolean => {
  if (arr.length === 0) return false
  const [head, ...rest] = arr
  if (head === tar) return true
  return includes(tar, rest)
}

타입 레벨에서 재귀(Recursion) 호출이 가능하다는것은 엄청나게 다양한 것을 가능하게 한다
예를들면, 순열을 만드는 함수 Permutation<T>를 만들 수 있다

type Permutation<T, U = T> = [T] extends [never] ? [] : (
  T extends U ? (
    [T, ...Permutation<Exclude<U, T>>]
  ) : []
)
type 결과 = Permutation<'A' | 'B' | 'C'>
// 결과 = ['A', 'B', 'C'] | ['A', 'C', 'B'] | ['B', 'A', 'C'] 
//     | ['B', 'C', 'A'] | ['C', 'A', 'B'] | ['C', 'B', 'A']

Distributive Conditional Types

Union 타입은 conditional 타입으로 분기검사를 할때 분배법칙으로 나눠지는 성질이 있다

type ToArray<T> =
  T extends any ? 👈 항상 참, any는 모든 집합의 상위집합이자 부분집합
    T[]
    : never
type 결과 = ToArray<string | number>;
//   결과 = string[] | number[]

이는 Union타입이 분배법칙에 의해서 아래처럼 분배되었기 때문이다

ToArray<string> | ToArray<number>
// 다음과 같이 환원될 것이다 
// string[] | number[]

만약에 (string | number)[]를 얻기를 원한다면 아래처럼 써야한다

type ToArray<T> = [T] extends [any] ? Type[] : never;

마무리

위에서 언급했던 타입 시스템이 할 수 있는것들을 다시한번 가져오겠다

타입 시스템이 할 수 있는것들

• 함수 ✅
• 분기 - Conditional Branching ✅
• 변수 대입 ✅
• 루프 - Loops ✅
• 동일성 체크 ✅

동일성 체크를 제외한 모든것을 다뤘다
동일성 체크는 약간의 과제로 남기며 끝내려고 한다

동일성 체크 (과제)

동일성을 체크하는 Equal<T, Q> 함수를 만들어봐라
단, Equal함수는 인자로 any타입을 받을 수 있고, any타입에 무너지면 안된다

type Equal<T, Q> = 여기_코드_작성

type V1 = Equal<1, any> // should be false
type V2 = Equal<1, 1> // should be true
type V3 = Equal<1, 0> // should be false
type V4 = Equal<any, any> // should be true
type V5 = Equal<{ a: 10 }, { a: 20 }> // false
type V6 = Equal<{ a: 10 }, { a: 10 }> // true
type V7 = Equal<[1, 2, 3], [1, 2, 3]> // true
type V8 = Equal<[1, 2, 3], [any, 2, 3]> // false
type V9 = Equal<[], []> // true
type V10 = Equal<[1, 2], [1, 2, 3]> // false
type V11 = Equal<1 | 2 | 3, 2 | 3 | 1> // true
type V12 = Equal<1 | 2, 1 | 3 | 2> // false

type ExpectTrue<T extends true> = T
type ExpectFalse<T extends false> = T

type tests = [
  ExpectFalse<V1>,
  ExpectTrue<V2>,
  ExpectFalse<V3>,
  ExpectTrue<V4>,
  ExpectFalse<V5>,
  ExpectTrue<V6>,
  ExpectTrue<V7>,
  ExpectFalse<V8>,
  ExpectTrue<V9>,
  ExpectFalse<V10>,
  ExpectTrue<V11>,
  ExpectFalse<V12>,
]

힌트를 조금 주자면 아래 코드를 생각해보는것 부터 시작해라

type Equal<T, Q> = 
  T extends Q ? (
    Q extends T ? true : false
  ) : false

동일성 체크를 구현한다면 아래처럼 테스트 코드를 먼저 작성하고 타입을 작성하는 TDD를 할 수 있다

type KebabCase<T extends string, P extends string> = 
  아직_작성하지_않은_함수

type Expect<T extends true> = T

type cases = [
  Expect<Equal<KebabCase<'FooBarBaz'>, 'foo-bar-baz'>>,
  Expect<Equal<KebabCase<'fooBarBaz'>, 'foo-bar-baz'>>,
  Expect<Equal<KebabCase<'foo-bar'>, 'foo-bar'>>,
  Expect<Equal<KebabCase<'foo_bar'>, 'foo_bar'>>,
  Expect<Equal<KebabCase<'Foo-Bar'>, 'foo--bar'>>,
  Expect<Equal<KebabCase<'ABC'>, 'a-b-c'>>,
  Expect<Equal<KebabCase<'-'>, '-'>>,
  Expect<Equal<KebabCase<''>, ''>>,
  Expect<Equal<KebabCase<'😎'>, '😎'>>
]

참고한 자료들

• 공식문서, typescriptlang.org
• Type Level Programming in TypeScript by Gabriel Vergnaud
  
• type-challenges
• O'REILLY사의 책: 함수형 사고
• 유튜브: 너희는 전혀 스윙하고 있지 않아
• 위키피디아: 튜링완전성
• TS깃헙: 튜링완전성증명
• 타입레벨 소코반게임
• 위키피디아: 공리
• 나무위키: 논리회로
• 네이버블로그: 카르노맵
• 타입스크립트의 공변성과 반공변성: 육지수님 번역
• 리스코프 치환 원칙과 공변성, 반공변성에 대해 알아보자: Roseline님 블로그
• 타입레벨 고차함수 by overcurried
• Equal